模拟集成电路设计系列博客——7.5.1 积分型ADC

7.5.1 积分型ADC

积分型ADC是一种流行的对于慢速信号做高精度数据转换的方式。这类ADC有着非常低的失调与增益误差，且高度线性。更进一步的优势是积分型ADC在实现时仅仅需要很少的电路。积分型ADC的一个常用场景是用在测量仪器中，例如电压表或者电流表。

双斜积分型ADC的简化架构图如下图所示：

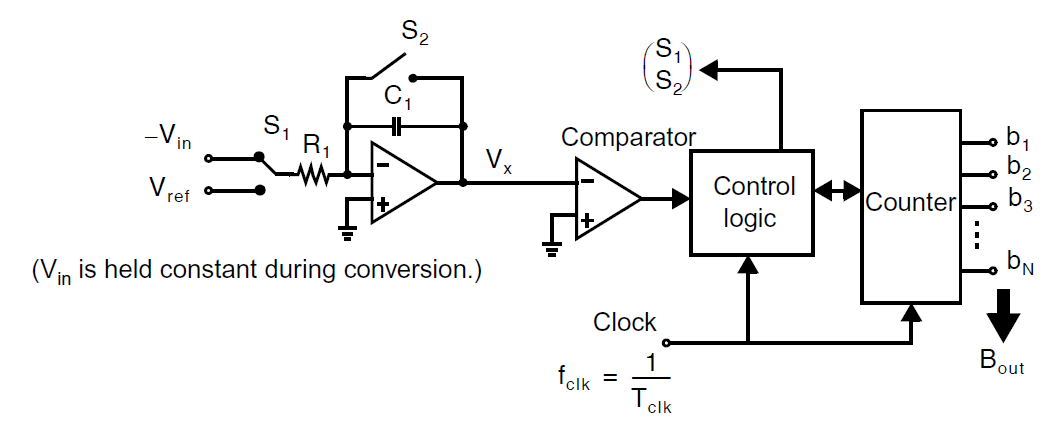
双斜的意思是指这个ADC通过两个阶段完成转换，阶段Ⅰ和阶段Ⅱ，如下图所示：

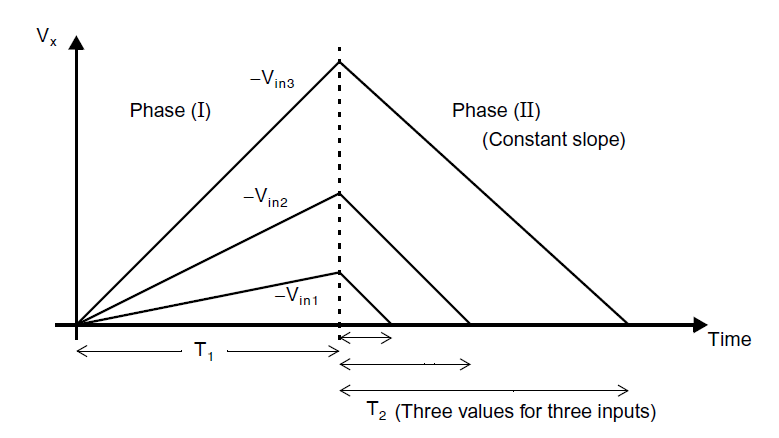
阶段Ⅰ：阶段Ⅰ时间间隔固定为\(T_1\)，通过运行\(2^N\)个时钟周期得到，因此我们有：

\[T_1=2^NT_{clk} \tag{7.5.1} \]

其中\(T_{clk}\)是一个时钟周期，在这个间隔中，开关\(S_1\)连接到\(-V_{in}\)，从而\(V_x\)跟随\(V_{in}\)的幅度上升。假定\(V_x\)一开始等于零（通过\(S_2\)上的一个脉冲），\(V_{in}\)保持固定，我们会有如下的关系式：

\[V_x(t)=-\int_{0}^t\frac{-V_{in}}{R_1C_1}d\tau=\frac{V_{in}}{R_1C_1}t \tag{7.5.2} \]

因此，在阶段Ⅰ结束时，\(V_x\)会等于\(V_{in}T_1/R_1C_1\)。

阶段Ⅱ：阶段Ⅱ的时间是变化的\(T_2\)，上图中展示了对于三种不同的输入电压的情况。在阶段Ⅱ一开始，计数器复位，\(S_1\)被连接到\(V_{ref}\)，使得\(V_x\)电压开始以固定的斜率下降。为了求得数字输出值，计数器持续计数，直到\(V_x\)小于零，此时计数器值会等于输入信号\(V_{in}\)的数字码。因此，假定数字输出值做了归一化，最大值为单位值，计数器输出\(B_{out}\)可以被定义为：

\[B_{out}=b_12^{-1}+b_22^{-2}+...+b_{N-1}2^{-(N-1)}+b_N2^{-N} \tag{7.5.3} \]

从而我们有：

\[T_2=2^NB_{out}T_{clk}=(b_12^{N-1}+b_22^{N-2}+...+b_{N-1}2+b_N)T_{clk} \tag{7.5.4} \]

为了直到为什么计数器会给出正确的值，我们求解\(V_x\)在第Ⅱ阶段时的方程：

\[V_x(t)=-\int_{T_1}^t\frac{V_{ref}}{R_1C_1}d\tau +V_{x}(T_1)=\frac{-V_{ref}}{R_1C_1}(t-T_1)+\frac{V_{in}T_1}{R_1C_1} \tag{7.5.5} \]

当\(V_x\)为零时，\(t=T_1+T_2\)，我们可以写出：

\[0=\frac{-V_{ref}T_2}{R_1C_1}+\frac{V_{in}T_1}{R_1C_1} \tag{7.5.6} \]

求解该方程可以得到：

\[T_2=T_1(\frac{V_{in}}{V_{ref}}) \tag{7.5.7} \]

结合\((7.5.7)\)，\((7.5.1)\)和\((7.5.4)\)，我们有：

\[B_{out}=b_12^{-1}+b_22^{-2}+...+b_{N-1}2^{-(N-1)}+b_N2^{-N}=\frac{V_{in}}{V_{ref}} \tag{7.5.8} \]

从上式中，我们可以看到对于双斜转换，数字输出并不依赖于时间常数\(R_1C_1\)，这个时间常数只需要能够在单次转换中保持稳定即可正常工作。当时\(R_1\)和\(C_1\)需要被合理的选取，从而可以使得\(V_x\)取得足够大的峰值，而不需要采取操作来减小噪声的影响。也可以通过单斜转换实现ADC，这样只需要一个转换阶段，但是积分时间就需要是时间常数\(R_1C_1\)的函数，非常可能出现增益误差。

尽管双斜积分型ADC不会受到增益误差的影响，但是它可能会收到放大器失调和其他因素导致的失调错误。这个失调错误可以通过使用四斜转换来进行矫正。在四斜转换中，双斜转换被执行两次：第一次时输入被连接到地（或者任何已知的直流量），然后输入被连接到待转换的信号\(V_{in}\)。两次输出码相减就可以将失调错误减少到零。

这类转换器的转换速度非常慢，例如，在双斜ADC中，最坏情况下的转换速率为\(V_{in}\)等于\(V_{ref}\)，这种情况下需要\(2^{N+1}\)个时钟周期来完成转换。因此对于16 bit转换器来说，如果其时钟为\(1MHz\)，那么最坏情况下的转换速率只有\(7.6Hz\)。

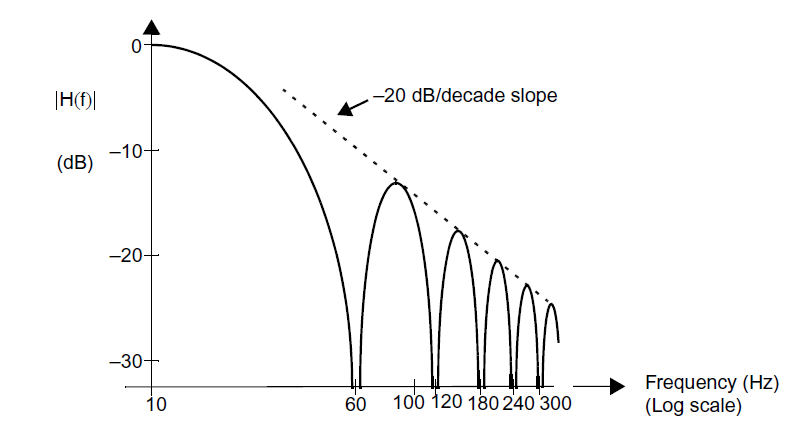
最后，需要注意的是，通过精心选择\(T_1\)，叠加在输入信号上的某些频率分量可以得到显著的衰减。注意这个转换器实际上对输入信号做了“积分与存储”，如果我们放松之前对\(V_{in}\)是常数的假设，我们可以看到转换\(V_{in}\)的过程实际上相当于是在一个时间窗\(T_1\)内对\(V_{in}\)做积分：

\[\int_{0}^{T_1}\frac{V_{in}(\tau)}{R_1C_1}d\tau \tag{7.5.9} \]

等效于和一个矩形时间窗口做卷积。由于矩形脉冲的傅里叶变换为\(sin(x)/x\)，我们可以得到等效的输入滤波器的传输函数：

\[|H(f)|=|\frac{sin(\pi f T_1)}{\pi f T_1}| \tag{7.5.10} \]

因此，积分转换器也有着低通响应，并且在\(f=1/T_1\)的整数倍上时为零。

事实上其他的频率也会被衰减，只是不会和\(1/T_1\)的谐波一样被完全抑制，如下图的频谱所示，越是高频收到的衰减越大：