模拟集成电路设计系列博客——7.4.5 多比特Σ-Δ ADC
7.4.5 多比特Σ-Δ ADC
尽管1bit过采样ADC有着可以实现高线性度的优点,但其也有一些缺点。例如,动态范围小;1bit过采样ADC可能会由于反馈中的高度非线性出现不稳定;还有闲音(idle tones)的问题,即当输入信号接近直流或者是一个幅值为很小的正弦波时,在输出端就会产生一个很明显的tone。使用多比特DAC可以优化缺点,但是必须通过精心设计来确保多比特ADC保持线性。一个典型的多比特过采样ADC系统与1bit的系统架构类似,主要是在调制器中会使用一个M bit的量化器,且其输出会驱动一个M bit的DAC。这一节会讨论一些多比特过采样ADC的架构,以及一些让整体系统保持高度线性的方法。
一种在过采样ADC里使用多比特DAC的方法是使用一个修正循环,其中数字电路用于建模DAC的静态非线性,如下图所示[Larson, 1988]:
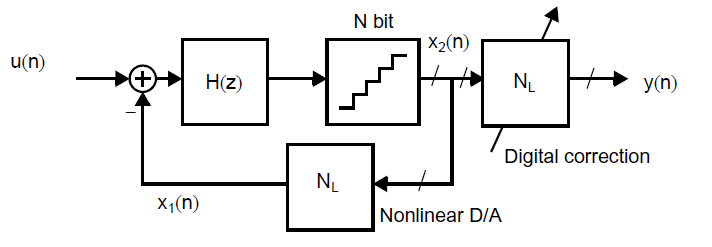
通过这种方式,多比特数字信号\(x_2(n)\)在\(x_1(n)\)处产生\(2^N\)个输出电平,在时间上一致,但是并不一定与\(x_2(n)\)呈线性。但是调制器的反馈回路强制使得\(x_1(n)\)的带内频率非常接近等于\(u(n)\),因此\(x_1(n)\)仍然与\(u(n)\)呈现线性相关。通过使用数字数字修正电路,如果其非线性与DAC相同,信号\(y(n)\)也会与\(x_1(n)\)相同。为了实现数字修正电路,一个\(2^N\)个字的查找表RAM被使用,其尺寸至少与想要实现的线性度相等。例如,如果使用了一个4 bi DAC,并且需要18 bit的线性度,那么数字修正电路需要由一个16字RAM组成,每个字需要至少有18 bit(或者等效的说288 bit的RAM)。更进一步的,RAM的尺寸可以通过仅仅将所需要的线性度和DAC的预期线性度之差进行数字化来减小[Sarhang-Nejad, 1993]。例如,如果DAC预期有至少9 bit的线性度,那么RAM仅仅需要有10 bit的字长来实现18 bit的整体线性度。
数字修正电路的校准可以通过将\(\Delta \Sigma\)调制器重配置为一个单比特系统来实现。1 bit转换器的输入是要校准的4 bit DAC电平之一。换而言之,当其输出被施加在1 bit AD调制器时,多比特转换器在多个时钟周期内保持固定。这使得1 bit信号被数字低通滤波,并且能够给出DAC特定直流值的所需要的数字等效值。这个过程被重复16次直到找到RAM的16个字。
另一种非常有趣的架构是同时使用多比特反馈和单比特反馈[Hairapetian, 1994]。下图展示了一个三阶ADC的例子:
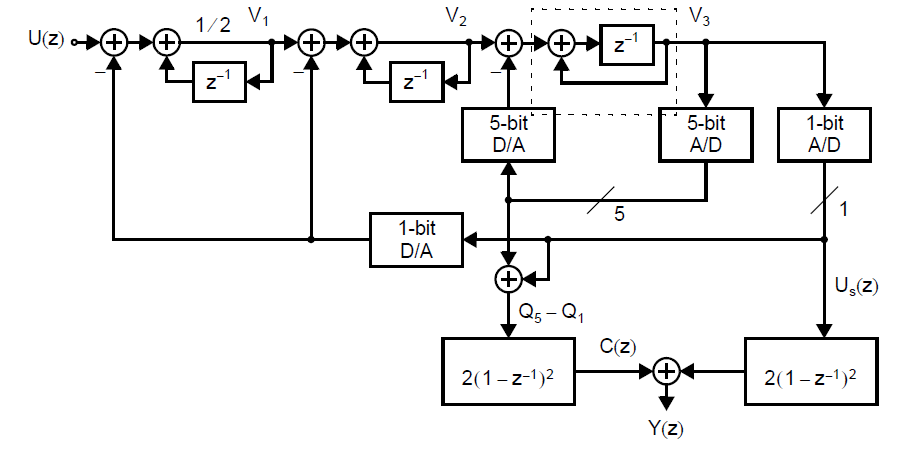
假定1 bit ADC和5 bit ADC的量化误差分别为\(Q_1\)和\(Q_5\),而5 bit DAC由于非线性注入的误差为\(Q_d\)。对上图中的系统做线性分析:
在数字信号处理之后,数字输出信号\(Y(z)\)为:
可以看出,基于理想积分器的假设,1 bit ADC的量化噪声可以完全消除,5 bit ADC的量化噪声收到了三阶的噪声整形,而5 bit DAC的非线性噪声收到二阶整形。当然,如果积分器不理想,那么1 bit ADC的量化噪声无法被完全取消,但是仍然会收到二阶噪声整形。可以看到这个系统的稳定性类似于二阶\(\Sigma\Delta\) ADC。需要注意的是数字信号处理不需要任何乘法,但是多比特信号必须跟随抽取器处理,导致其实现变得复杂。


