模拟集成电路设计系列博客——7.4.4 Σ-Δ ADC的抽取滤波器

7.4.4 Σ-Δ ADC的抽取滤波器

有许多在过采样ADC中实现数字抽取滤波器的方式，这里我们会介绍多级和单级两种流行方法。

首先介绍通过多级方法实现抽取滤波器，如下图所示：

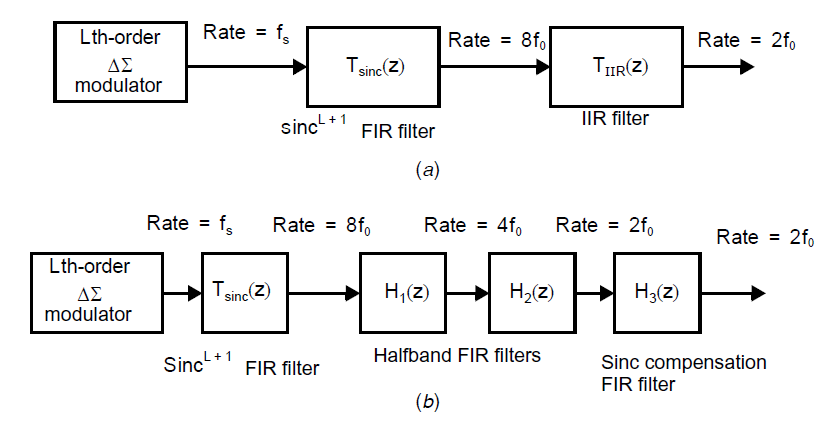
此处，第一级的FIR滤波器\(T_{sinc}(z)\)消除了许多量化噪声，使得其输出可以降采样到奈奎斯特频率的四倍（即\(8f_0\)）。低速率的输出被送入第二级滤波器，有可能是一个上图(a)中的IIR滤波器，也有可能是(b)中的级联FIR滤波器。

\(sinc^{L+1}\)FIR滤波器是\(L+1\)个均值滤波器的级联，其中均值平均滤波器传输函数\(T_{avg}(z)\)为：

\[T_{avg}(z)=\frac{Y(z)}{U(z)}=\frac{1}{M}\sum_{i=0}^{M-1}z^{-i} \tag{7.4.24} \]

\(M\)为\(f_s\)对\(8f_0\)的整数比（即\(8f_0=f_s/M\)）。注意这个滤波器的冲激响应是有限的，因此是一个FIR滤波器。此外，其冲激响应因子均为对称的（事实上它们全部相等），因此它也是一个线性相位滤波器。最后，注意这个\(1/M\)因子项很容易通过改变截断比特来改变，只要\(M\)取得是2的指数倍。

为了展示一系列的均值滤波器如何减小量化噪声，考虑一个4均值滤波器(\(M=4\))，其输入为一比特序列序列\(\{1,1,-1,1,1,-1,1,1,-1,...\}\)，第一次平均后的输出\(x_{lp1}(n)\)为：

\[x_{lp1}(n)=\{0.5,0.5,0.0,0.5,0.5,0.0,...\} \tag{7.4.25} \]

为了进一步缓解量化噪声，信号\(x_{lp1}(n)\)可以进一步再送入一个4均值滤波器得到\(x_{lp2}(n)\)：

\[x_{lp2}(n)=\{0.375,0.375,0.25,0.375,0.375,0.25,...\} \tag{7.4.26} \]

重复这个过程进一步得到\(x_{lp3}(n)\)：

\[x_{lp3}(n)=\{0.344,0.344,0.313,0.344,0.344,0.313,...\} \tag{7.4.27} \]

可以发现整个采样序列逐渐向预期的\(1/3\)收敛。

为了展示均值滤波器的频域响应\(T_{avg}(z)\)有着\(sinc\)的行为，可以将\((7.4.24)\)重写为：

\[MY(z)=(\sum_{i=0}^{M-1}z^{-i})U(z)=(1+z^{-1}+z^{-2}+...+z^{-(M-1)})U(z) \tag{7.4.28} \]

可以重写为：

\[MY(z)=(z^{-1}+z^{-2}+...+z^{-M})U(z)+(1-z^{-M})U(z)\\=Mz^{-1}Y(z)+(1-z^{-M})U(z) \tag{7.4.29} \]

最后我们可以求出均值滤波器的传输函数为：

\[T_{avg}(z)=\frac{Y(z)}{U(z)}=\frac{1}{M}(\frac{1-z^{-M}}{1-z^{-1}}) \tag{7.4.30} \]

这个滤波器的频率响应可以通过代入\(z=e^{j\omega}\)求得，为：

\[T_{avg}(e^{j\omega})=\frac{sinc(\omega M/2)}{sinc(\omega/2)} \tag{7.4.31} \]

其中\(sinc(x)=sin(x)/x\)。

对均值滤波器进行\(L+1\)级级联后传输函数\(T_{sinc}(z)\)为：

\[T_{sinc}(z)=\frac{1}{M^{L+1}}(\frac{1-z^{-M}}{1-z^{-1}})^{L+1} \tag{7.4.32} \]

将\(L+1\)级均值滤波器做级联的原因是低通滤波器的衰减率应当大于噪声量化函数的提升率，从而使得噪声能够被有效降低。否则噪声会分布在一个很宽的频带内，造成大的总噪声。

有个有效的实现这种级联均值滤波器的方式是将\((7.4.32)\)重写为：

\[T_{sinc}(z)=(\frac{1}{1-z^{-1}})^{L+1}(1-z^M)^{L+1}\frac{1}{M^{L+1}} \tag{7.4.33} \]

然后以下图的方式对齐做实现[Candy, 1992]：

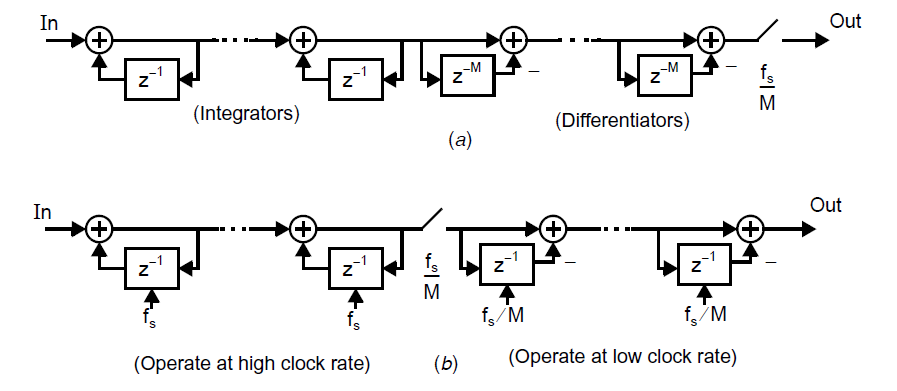
此处要注意的是，第一眼看这个电路并不能良好工作，因为直流输入会造成离散时间积分器的饱和。幸运的是，只要使用二的补码就不会出现这个问题。具体来说，尽管积分器输出的直流电平可能不对，但是微分器会将当前的采样与\(M\)次之前的采样进行比较，从而剪掉直流分量。因此，只要这个差是对的（如果使用二的补码那就不会出问题）就可以确保正确的计算。

再次回到上上图，\(T_{sinc}(z)\)滤波器后的滤波器的目的有两个。一个原因是在把信号降采样到最终的奈奎斯特频率之前（例如\(2f_0\)），使用它们来消除任何高频输入信号（即一个尖锐的抗混叠滤波器）。换而言之，尽管\(T_{sinc}(z)\)可以有效的滤除量化噪声，其作为一个抗混叠滤波器，对于输入信号略高于\(f_0\)的频率是不够尖锐的。第二个原因是要补偿\(T_{sinc}(z)\)滤波器导致的通带中下降的频率。可以如上上图(a)中用一个IIR滤波器同时实现抗混叠和\(sinc\)补偿滤波器。也可以如上图(b)所示，通过使用数个半带FIR滤波器和一个独立的\(sinc\)补偿FIR滤波器。半带FIR滤波器的通带从0到\(\pi/2\)，其止带为\(\pi/2\)到\(\pi\)，其偶数因子均为0 [Vaidyanathan, 1993]。因此，通过足够高的滤波器阶数，其输出可以通过两倍因子降采样。在一些应用中，这些半带滤波器和\(sinc\)补偿器可以使用非通用多位乘法器来实现[Saramaki, 1990]。

接下来看单级实现抽取滤波器的方案，一种方案是使用一个相对高阶的FIR滤波器。例如，在[Dattorro, 1989]中，一个2048头FIR滤波器被用于抽取来自两个\(\Delta \Sigma\)调制器的1bit码流，每个的降采样率为64。尽管这个FIR的阶数看上去很高，但是注意其并不需要多比特乘法，因为输入信号仅仅只有1bit，因此所有的乘法都可以省去。此外，输出仅仅需要以奈奎斯特频率进行计算（中间的采样都会被丢弃），因此最终需要奈奎斯特频率下，一个时钟周期内的2048个加法。然而，如果只用一个累加器来执行所有的2048次加法，累加器的时钟速率需要2048倍于奈奎斯特频率。例如，如果奈奎斯特频率\(48kHz\)，单么这个累加器需要以\(98.3MHz\)时钟工作。为了克服这个高速时钟的问题，最终实现了32个独立的FIR滤波器（共享因子）以时间交错方式工作，每个FIR有2048个因此，每个以\(1.5kHz\)的时钟处理输出。在这个方式下，32个FIR滤波器中的每一个只需要使用一个工作在\(3MHz\)的累加器（\(1.5kHz\)的2048倍）。存储因子的ROM被所有的FIR滤波器共享，如果因子是对称的，那么ROM的尺寸还可以减半，就如在线性相位FIR滤波器中的情况。

最后，也可能可以通过将输入比特组合来减少加法的总数。例如，如果四个加法比特组合在一起，那么可以使用一个16个字的ROM查找表，而不是使用三个加法。通过这样的输入比特的组合，32个FIR滤波器中的每一个只需要做512次加法。