模拟集成电路设计系列博客——6.2.2 基于R-2R的DAC

6.2.2 基于R-2R的DAC

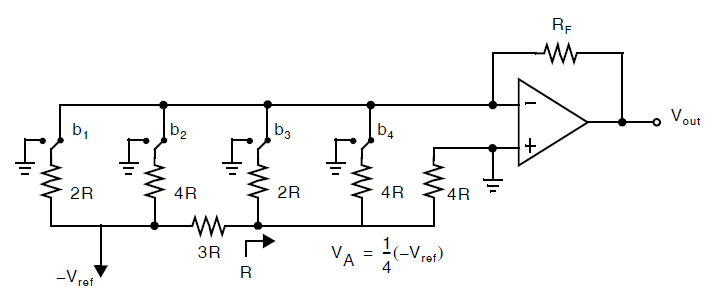
为了避免二进制权重转换器中的巨大电阻比例，可以通过引入串联电阻来使得阵列中的信号缩放，如下图所示：

注意此处的节点电压\(V_A\)等于参考电压\(V_{ref}\)的四分之一，作为\(3R\)的串联电阻引入的结果。同时注意一个额外的\(4R\)被添加在地处，从而使得从\(3R\)电阻右侧看入的电阻等于\(R\)。直接的分析显示，这个转换器与之前介绍的二进制权重转换器一样，有着与二进制数字码相同的关系，但是电阻比例却只有四分之一。然而，需要注意的是电流比例仍然是不变的。最后需要注意的是，通过重复这个过程形成一个二进制权重梯，最终可以得到一个\(R-2R\)梯型电阻转换器。

在D/A转换器中，\(R-2R\)梯型结构很常用。使用其可以在很少的组件，以及只有2的电阻比例下实现二进制权重，而不需要管总的比特位数\(N\)。

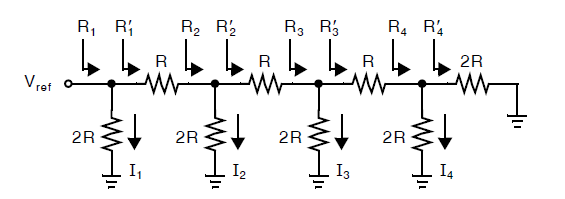
考虑如下图所示的\(R-2R\)梯型结构：

对其进行分析如下：

\[R_4^{'}=2R \tag{6.2.3} \]

\[R_4=2R||2R=R \tag{6.2.4} \]

\[R_3^{'}=R+R_4=2R \tag{6.2.5} \]

\[R_3=2R||R_3^{'}=R \tag{6.2.6} \]

以此类推，可以推导出对于所有的\(i\)，都有\(R_i^{'}=2R\)，因此这个结果将导出：

\[I_1=\frac{V_{ref}}{2R} \tag{6.2.7} \]

而节点二的电压为节点一的一半，因此：

\[I_2=\frac{V_{ref}}{4R} \tag{6.2.8} \]

在节点三，节点电压又被分为了一半，因此：

\[I_{3}=\frac{V_{ref}}{8R} \tag{6.2.9} \]

以此类推。

因此\(R-2R\)梯型结构可以仅使用单一尺寸的电阻来实现二进制权重电流（\(2R\)的电阻可以使用两个\(R\)尺寸的电阻进行组合来提升匹配特性）作为结果，\(R-2R\)方式一般来说相比二进制权重方式可以有更小的尺寸和更好的精度。

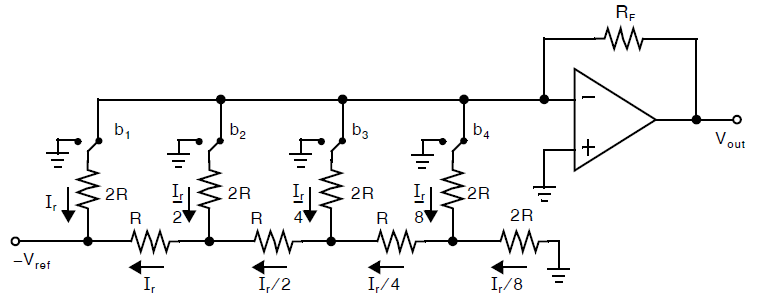
下图展示了一个\(R-2R\)梯型的4-bit的转换器：

我们可以得到：

\[I_r=V_{ref}/(2R) \tag{6.2.10} \]

以及：

\[V_{out}=R_F\sum_{i=1}^N(\frac{b_iI_r}{2^{i-1}})=V_{ref}(\frac{R_F}{R})\sum_{i=1}^N\frac{b_i}{2^i} \tag{6.2.11} \]

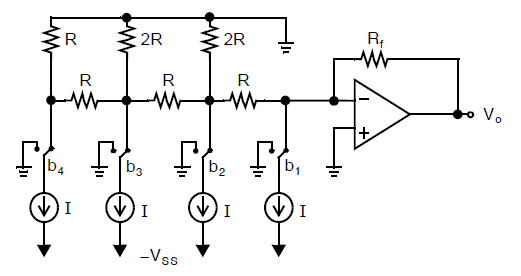
然而，正如之前所说，尽管电阻的比例被减小了，但是开关之间的电流比例仍然巨大，因此开关的尺寸必须跟着缩放来适应广泛的电流值。一种减小电流比例的方式如下图所示，开关上流经的所有电流都是相等的。但是这个结构变得更慢，因为现在\(R-2R\)梯型结构的内部节点出现了电压摆动（与之相对的，上图中的所有内部节点保持在一个固定的电压）：