模拟集成电路设计系列博客——5.4 其他开关电容电路
模拟集成电路设计 5.4 其他开关电容电路
5.4.1 其他开关电容电路
在本节我们将介绍一系列其他的可以用于非线性应用的开关电容电路。具体来说,我们会关注幅度调制器,全波整流器,峰值探测器,压控振荡器和正弦振荡器。
幅度调制器用于将一个信号沿着频率轴移动。例如,为了把一个信息信号\(m(t)\),移动到一个载波频率\(\omega_{ca}\)上,我们将\(m(t)\)与一个频率为\(\omega_{ca}\)的余弦信号相乘,数学上即:
由于\(cos(\omega_{ca}t)\)的傅里叶变换是\(\pi \delta (\omega-\omega_{ca})+\pi \delta (\omega+\omega_{ca})\),时域内的乘法等效为频域内的卷积,可以将\(y(t)\)的频谱写为:
因此,频谱只在\(\pm \omega_{ca}\)有能量。
然而,在很多情况下,难以实现一个正弦信号,以及一个线性乘法器。作为结果,一般调制器利用方波作为载波信号,在这种情况下输出信号为:
其中\(S_q(t)\)是一个工作在载波频率的方波,幅度被归一化为1.因此,这个方式仅仅需要一个载波频率的方波来巨顶到底是\(m(t)\)还是\(-m(t)\)传输到输出。但代价是,相比\(Y(\omega)\)只在\(\pm \omega_{ca}\)附近有能量,使用方波载波会使得在\(\pm \omega_{ca}\)的奇数频率附近也有显著的能量,因为方波信号在基波的奇次谐波处也有能量。这些额外的谐波可以通过使用额外的滤波级来消除。
方波调制器可以通过开关电容技术来实现,如下图所示:
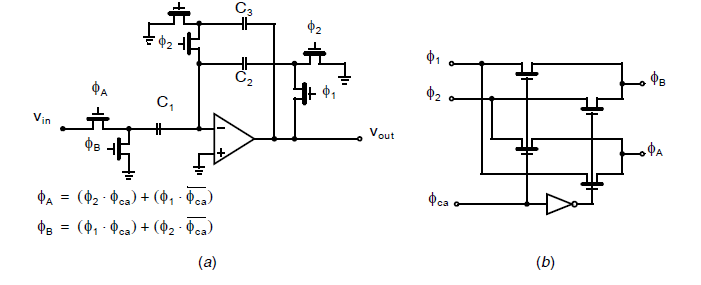
此处调制器通过使用之前介绍过的电容重置增益电路实现,如上图中(a)所示。注意输出信号的极性通过改变输入晶体管的时钟相位\(\phi_A\)和\(\phi_B\)来改变,这两个信号通过方波载波时钟信号\(\phi_{ca}\)来控制,当\(\phi_{ca}\)为高,\(\phi_A=\phi_2\),\(\phi_B=\phi_1\),结果为正相输出\((C_1/C_2)v_{in}\)。当\(\phi_{ca}\)为低,\(\phi_A\)和\(\phi_B\)的相位切换,电路产生反相输出\(-(C_1/C_2)v_{in}\),时钟相位控制电路如上图(b)所示。
全波整流器产生的输出是输入的绝对值,换而言之,如果输入是正的,那么输出等于输入,如果输入是负的,那么输出等于输入的取反。
可以使用幅度调制器来实现一个全波整流器,不需要使用方波载波信号,取而代之的是一个控制输出信号极性的比较器,如下图所示:
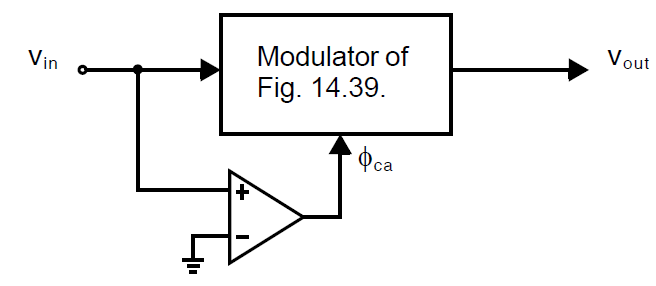
如果输入信号高于地,\(\phi_{ca}\)为高,输出等于输入的一个线性缩放版本。如果输入信号低于地,\(\phi_{ca}\)为低,输出等于输入版本的反相线性缩放。为了正确工作,比较器输出必须和采样器件同步改变。这个工作电路可以参考[Gregorian,1986]。
峰值检测器的输出是输入信号在一段时间里的最大值。尽管峰值检测器一般有一些关联的衰减电路(或者是一个重置峰值的电路),此处我们只关注峰值检测器本身。两种实现峰值检测器的方式如下图所示:
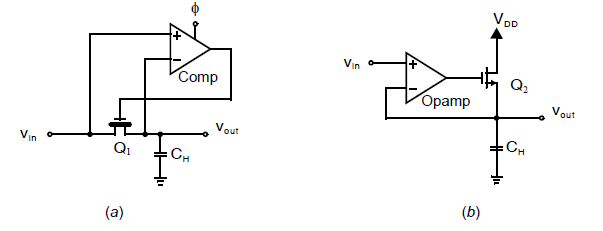
在上图(a)中,一个锁存比较器用于比较何时\(v_{in}>v_{out}\),当满足这个条件时,比较器输出拉高,开关\(Q_1\)打开,使得\(v_{out}=v_{in}\)。比较器使用锁存的目的,一方面是为了保证速度,另一方面是确保比较器输出要么是低要么是高。注意这个电路需要输入信号直接穿过\(Q_1\)驱动\(C_H\),因此可能需要缓冲电路。但是这个电路可以非常的快,因为锁存比较器可以做的很快,并且这里不涉及放大器建立(只有\(Q_1\)和\(C_H\)形成的RC时间常数)。
上图(b)中的电路需要一个放大器(需要被良好补偿),由于其将\(Q_2\)放置在一个反馈连接中,当\(v_{in}>v_{out}\),放大器输出开始升高,因此打开\(Q_2\),从而打开反馈环路。当反馈环路打开时,很高的开环增益会使得\(v_{out}=v_{in}\)并且非常精确。注意这个电路有着很大的输入阻抗,因为信号被施加在放大器的正极。但是,这个基于放大器的电路会比(a)中的基于比较器的电路慢很多,因为需要等待放大器输出的摆动和建立。这个摆动时间可以通过增加确保\(Q_2\)不导通时\(Q_2\)的栅极永远不会变得比输出电压低的电路来减小。
压控振荡器(VCO)是一个通过控制电压来调整频率的振荡器,我们会看到,此处描述的压控振荡器产生的输出方波将交替处于两个状态之一,因此也被叫做弛豫振荡器。压控振荡器是锁相环(PLL)的一个组件。
弛豫振荡器的基本原理和典型波形如下图所示[Martin,1981]:
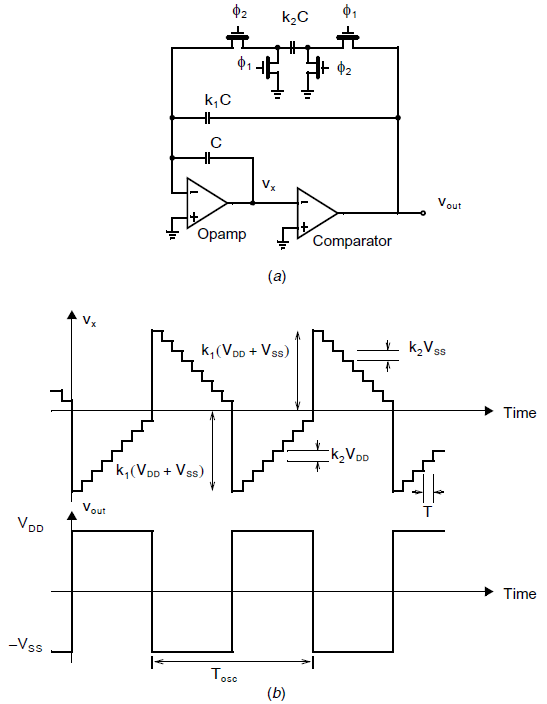
其工作原理为,假定\(v_{out}\)切换为低,到达了\(-V_{SS}\),并且节点\(v_x\)现在处于一个略高于零的电平。在\(\phi_1\),\(k_2C\)会被充电到电压为\(-V_{SS}\),使得其电荷值为:
注意非开关电容\(k_1C\)两端的电压保持在\(-V_{SS}\)不变,接下来,当\(\phi_2\)升高,\(k_2C\)上的电荷会被传输到\(C\)(而\(k_1C\)两端的电压仍然保持不变),\(v_x\)会变化如下的值:
这个操作会持续到直到\(v_x\)达到零电压。此处\(k_2C\)和\(C\)形成了一个正相离散时间积分器,而电容\(k_1C\)并不影响电路的工作。一旦\(v_x\)降低到零以下,比较器的输出会切换到\(V_{DD}\),在这个时间点,大量的电荷会流经\(k_1C\),其两端的电压从\(-V_{SS}\)变为\(V_{DD}\),这个巨大的电荷值等于:
由于这个电荷会流通\(C\),因此\(\Delta Q_{C}=\Delta Q_{k1C}\),因此节点电压\(v_x\)会变化如下的值:
如上图中(b)所示。在这之后,\(v_x\)将会以\(k_2V_{DD}\)的幅度阶跃(因为此时\(v_{out}\)现在等于\(V_{DD}\)),直到\(v_x=0\),在这个点会产生一个很大的正向电压阶跃。在这个正向阶跃之后,我们会回到起始点,整个开始循环往复。
为了得到振荡器周期\(T_{osc}\)的公式,我们假定\(k_1>>k_2\),从而在一半\(T_{osc}\)内会出现许多小阶跃。带着这个假设,我们现在可以写出时钟周期的总数\(T_{osc}/T\),等于\(v_x\)下摆时的节约数量加上\(v_x\)上摆时的阶跃数量。从数学上,我们有:
假定\(V_{DD}=V_{SS}\),我们得到占空比为百分之50的方波,其周期为:
从而:
这个固定频率的振荡器可以通过加入一个额外的馈入电容来实现压控,如下图所示:
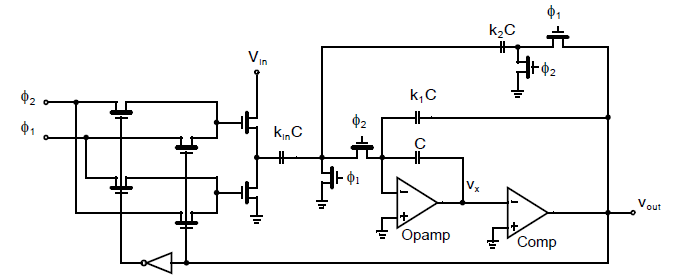
此处,当\(V_{in}\)为正,与\(k_2C\)同极的额外的电荷被注入到积分器中,因此这个电路更快的达到\(v_x=0\)。如果\(V_{in}\)为负,那么\(k_2C\)相反极性的电荷被注入到积分器中,因此这个电路更慢的达到\(v_x=0\)。假定\(k_1>>k_2,k_{in}\),\(V_{DD}=V_{SS}\),这个压控振荡器的频率由下式给出:
在许多应用中,实现一个产生近似正弦输出的振荡器是非常有用的。例如,当按下按键式电话上的按钮时,通过电话线发送的信号只是特定频率的两个正弦信号(该信号称为双音多频 (DTMF) 信号)之和。因此,开关电容正弦振荡器可用于产生必要的按键信号。
一种产生正弦信号的方式如下图所示:
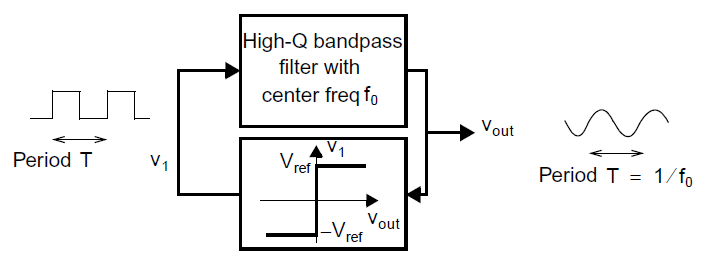
此处,一个中心频率为\(f_0\)的高\(Q\)带通滤波器与一个比较器一起使用,假定存在启动电路使得振荡器起振,我们会看到\(v_{out}\)处的正弦波会在\(v_1\)处产生一个方波,并且其在\(f_0\)有一个很大的频率分量。信号\(v_1\)通过带通滤波器滤波后产生正弦信号\(v_{out}\)。振荡器频率通过带通滤波器的中心频率来设置,而正弦信号的幅度则由滤波器的中频增益以及方波信号的峰值来决定。
这个电路的开关电容电路实现版本如下图所示:
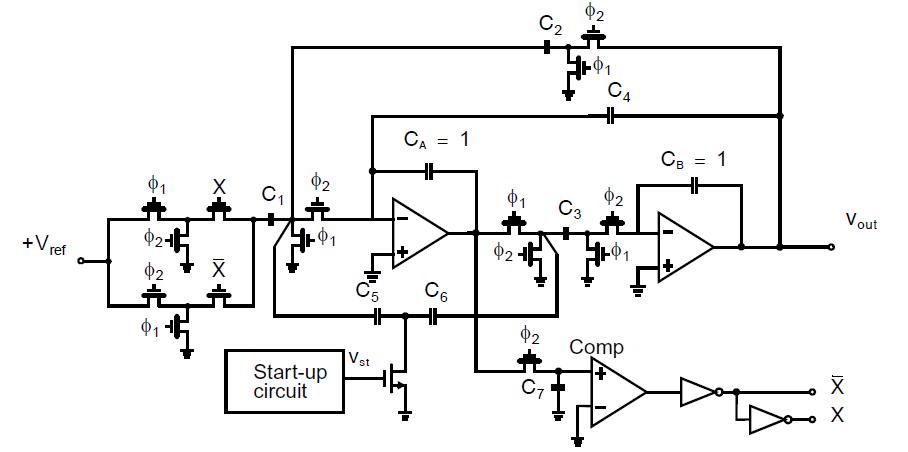
高\(Q\)带通滤波器通过之前介绍过的二阶开关电容滤波器电路实现,比较器通过与\(V_{ref}\)相关的开关输入是正还是负来产生\(X\)与\(\bar{X}\)。启动电路用来探查\(v_{out}\)上是否出现交流信号。当没有交流信号产生时,\(v_{st}\)为低,额外电容\(C_5\)和\(C_6\)形成一个正反馈环路使得振荡器起振。一旦检测到交流信号,\(v_{st}\)拉高,正反馈环路断开,之后振荡器如之前讨论的继续工作。


