模拟集成电路设计系列博客——5.2.1 一阶开关电容滤波器

5.2.1 一阶开关电容滤波器

在上一节我们讨论过，低频时，开关电容可以等效为电阻。利用这个等效，可以通过有源RC结构来推理设计出开关电容滤波器。然而，尽管这两种结构在低频输入信号（与时钟信号相比）时有着非常相似的表现。但是对于频率靠近时钟信号频率的输入信号来说。开关电容电路只能够通过\(z\)域的传输函数来精确表述。

一个通用的一阶有源RC滤波器如下图所示：

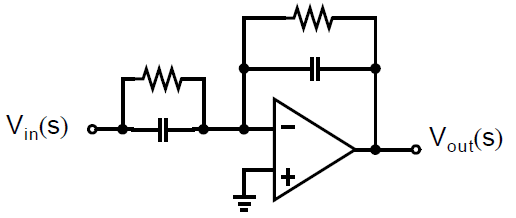
为了获得有相似低频响应的开关电容滤波器，电阻被替换成了无延迟的开关电容，而无开关的电容则保持不变。最终得到的开关电容滤波器以及其信号流图如下图所示：

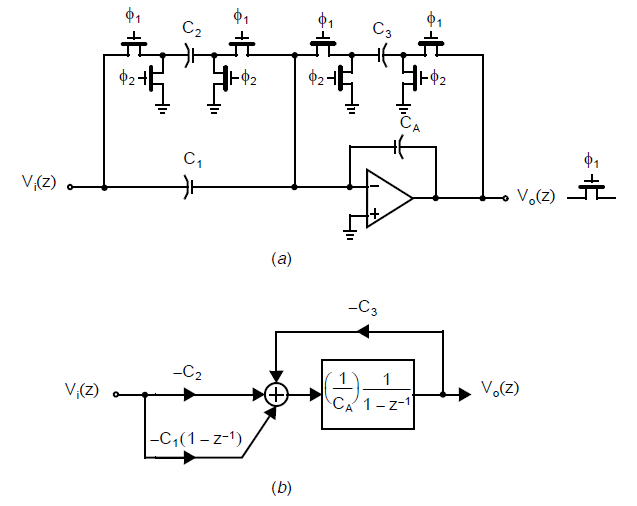
这里补充一下，在上一节我们讨论了寄生不敏感的延迟和无延迟积分器，里面用到的开关电容部分同样可以进行电阻等效，如下图所示：

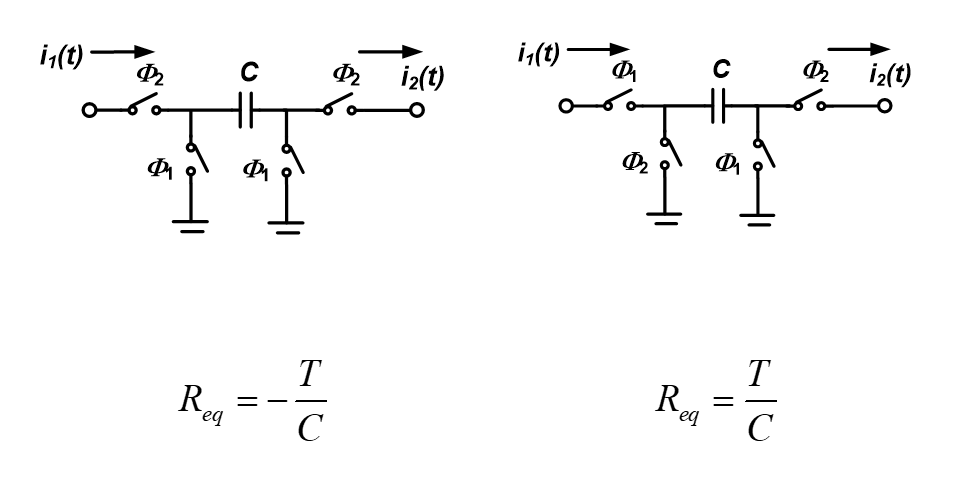
具体的推导与之前类似，设开关左侧电压为\(v_1\)，右侧电压为\(v_2\)，例如左边的电路，\(\phi_1\)打开时\(C\)两端电压为零，因此\(C\)上累积的电荷为零，\(\phi_2\)打开时，\(C\)上的电荷变为\(C(v_1-v_2)\)，因此变化的电荷量\(\Delta Q=0-C(v_1-v_2)=-C(v_1-v_2)\)，平均电流为\(I=\Delta Q/T=-C(v_1-v_2)/T\)，结合\(R_{eq}=(v_1-v_2)/I\)，结合两式可以得到\(R_{eq}=-T/C\)。对于右侧的电路用类似的方法可以推理出\(R_{eq}=T/C\)。

上面讨论的一阶滤波器可以写出离散时间z域方程：

\[C_A(1-z^{-1})V_o(z)=-C_3V_o(z)-C_2V_i(z)-C_1(1-z^{-1})V_i(z) \tag{5.2.1} \]

可以得到传输函数：

\[H(z)=\frac{V_o(z)}{V_i(z)}=-\frac{[(C_1+C_2)/C_A]z-C_1/C_A}{(1+C_3/C_A)z-1} \tag{5.2.2} \]

\((5.2.2)\)的极点\(z_p\)为：

\[z_p=\frac{C_A}{C_A+C_3} \tag{5.2.3} \]

注意到对于正的电容值，极点被限制在零和一之间的实轴，因此电路始终稳定。事实上，当\(C_3=0\)时，电路的极点位于\(z=1\)，或者说其变成了一个离散时间积分器。\((5.2.2)\)的零点位置\(z_z\)为：

\[z_z=\frac{C_1}{C_1+C_2} \tag{5.2.4} \]

因此，对于正电容值，零点位置也被限制在零到一的实轴之间。此外令\(z=1\)可以得到这个电路的直流增益：

\[H(1)=-\frac{C_2}{C_3} \tag{5.2.5} \]

在全差分电路中，可以通过交叉输入线来实现负的等效\(C_1\)，\(C_2\)，\(C_3\)，为了将\(z=-1\)设为零点，可以通过：

\[C_1=-0.5C_2 \tag{5.2.6} \]

换而言之，表示\(C_1\)的电容对是表示\(C_2\)的电容对的一半，输入项交叉到\(C_1\)对时，\(-V_i(z)\)被施加到输入分支上。

例题1：

找到实现一个\(-3dB\)点在\(10kHz\)的一阶开关电容滤波器电路的电容值，时钟频率为\(100KHz\)。滤波器在\(50KHz\)时为零增益，直流增益为单位增益。假定\(C_A=10pF\)。

解答：

首先注意到在\(50kHz\)时为零增益，等效于在\(-1\)处放置了一个零点。使用双线性变换\(p=(z-1)/(z+1)\)，可以知道\(z=-1\)处的零点对应\(\Omega=\infin\)。此外，根据两个域之间的频率变化，\(\Omega = tan(\omega/2)\)，将\(z\)域\(10KHz\)（或者说\(0.2\pi\) \(rad/sample\)）处的\(-3dB\)点转换到连续时间域：

\[\Omega = tan(\frac{0.2\pi}{2})=0.3249 \tag{5.2.7} \]

因此目前我们将分析简化为了找到一个\(-3dB\)频率为\(0.3249rad/s\)，零点为\(\infin\)的连续时间滤波器的极点位置。显然连续时间极点\(p_p\)为：

\[p_p=-0.3249 \tag{5.2.8} \]

将其映射回\(z\)域，可以得到：

\[z_p=\frac{1+p_p}{1-p_p}=0.5095 \tag{5.2.9} \]

因此，需要的离散时间传输函数\(H(z)\)为：

\[H(z)=\frac{k(z+1)}{z-0.5095} \tag{5.2.10} \]

进一步可以利用直流增益为单位增益的条件求出\(k\)（\(H(1)=1\)）：

\[H(z)=\frac{0.24525(z+1)}{z-0.5095} \tag{5.2.11} \]

\((5.2.11)\)等效为：

\[H(z)=\frac{0.4814z+0.4814}{1.9627z-1} \tag{5.2.12} \]

将这些因子代入到\((5.2.2)\)可以得到：

\[C_1=4.814pF \\ C_2 = -9.628pF \\ C_3 = 9.628 pF \tag{5.2.13} \]

其中负电容可以通过差分输入来实现。

对于零极点频率远低于时钟频率的设计（不像之前的例子，零点是时钟频率的一半），不需要通过双线性变换来进行求解，可以直接使用一些近似来通过给定的零极点（假定是实数和正数）求解电容比例方程，对于\((5.2.2)\)，我们有：

\[H(z)=\frac{V_o(z)}{V_i(z)}=-\frac{C_1/C_A(z^{1/2}-z^{-1/2})+C_2/C_Az^{1/2}}{z^{1/2}-z^{1/2}+C_3/C_A z^{1/2}} \tag{5.2.14} \]

进一步有：

\[H(e^{j\omega T})=\frac{V_o(e^{j\omega T})}{V_i(e^{j\omega T})}=-\frac{[j(2C_1+C_2)/C_A]sin(\omega T/2)+(C_2/C_A)cos(\omega T/2)}{j(2+C_3/C_A)sin(\omega T/2)+C_3/C_Acos(\omega T/2)} \tag{5.2.15} \]

利用\(\omega T <<1\)对\((5.2.15)\)进行简化，有：

\[H(e^{j\omega T})=\frac{V_o(e^{j\omega T})}{V_i(e^{j\omega T})}\approx-\frac{[j(C_1+C_2/2)/C_A]\omega T+C_2/C_A}{j(1+C_3/2C_A)\omega T+C_3/C_A} \tag{5.2.16} \]

这个过程对于找到一个近似离散传输函数的连续时间传输函数非常有用，令\((5.2.16)\)的分子为零可以求得零点频率的近似方程：

\[j\omega_zT=\frac{-C_2/C_1}{1+C_2/2C_1} \tag{5.2.17} \]

类似的，令分母为零可以得到极点的近似方程：

\[j\omega_pT=\frac{-C_3/C_A}{1+C_3/2C_A} \tag{5.2.18} \]

例题2：

利用近似方程，求一阶低通开关电容滤波器，\(C_1=0\)，极点为\(1/64\)采样频率时需要的\(C_3\)，低频增益为单位增益。

解答：

根据\((5.2.18)\)，求解\(C_3/C_A\)，可以得到：

\[C_3/C_A=\frac{\omega_p T}{1-\omega_pT/2}=\frac{2\pi/64}{1-2\pi/128}=0.1032 \tag{5.2.19} \]

如果我们选择\(C_A=10pF\)，那么\(C_3=1.032pF\)，根据\((5.2.16)\)，当\(C_1=0\)，我们知道低频增益由\(C_2/C_3\)给定，为了实现单位增益，我们需要\(C_2=1.032pF\)。

仔细研究之前介绍得到开关电容滤波器，可以发现有一些开关是冗余的。具体来说，\(C_2\)和\(C_3\)的顶极板总是同时在放大器的虚地和地之间切换。因此，这对开关可以去掉，将\(C_2\)和\(C_3\)的顶极板短接在一起，如下图所示：

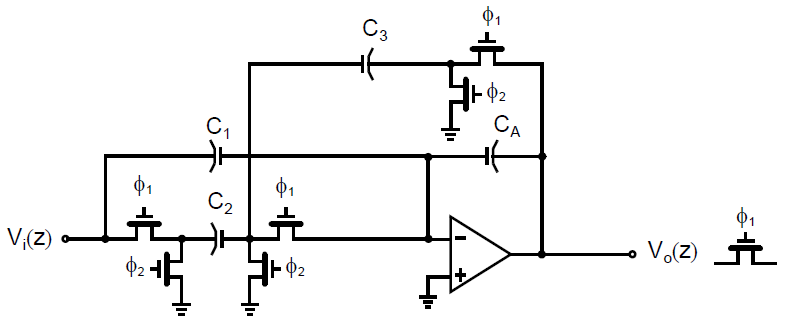
我们目前讨论过的电路都是处理单端信号的，但是在大部分模拟应用中需要信号为全差分。全差分信号意味着在两个信号线上做差，因此共模噪声不会影响信号。全差分信号需要是平衡的，这意味着差分信号对称的围绕一个直流共模电压（一般是模拟地，或者是电源供电电压的一半）。采用平衡的原因是因为由于对称性，噪声更可能是共模的。全差分电路的额外好处是可以抑制偶次失真项，这一点我们之前介绍全差分电路时讨论过，此处不做赘述。

下图展示了一个全差分一阶开关电容滤波器。注意全差分版本的电路实际上是复制了两份单端版本电路，所以一种理所当然的观点是这个电路会消耗两倍的面积。幸运的是，需要增加的面积开销没有那么大。首先我们注意到只需要一个放大器（尽管需要增加额外的共模反馈电路），其次，注意到输入和输出信号摆幅变为两倍，例如，如果单端信号的摆幅是正负一，那么单端信号的峰到峰摆幅为\(2V\)，而对于差分信号来说是\(4V\)，因此，由于\(kT/C\)噪声需要维持相同的动态范围时，全差分电路的电路只需要是单端电路的一半。由于使用了更小的电容，开关的尺寸也可以减少来满足相同的建立时间需求。

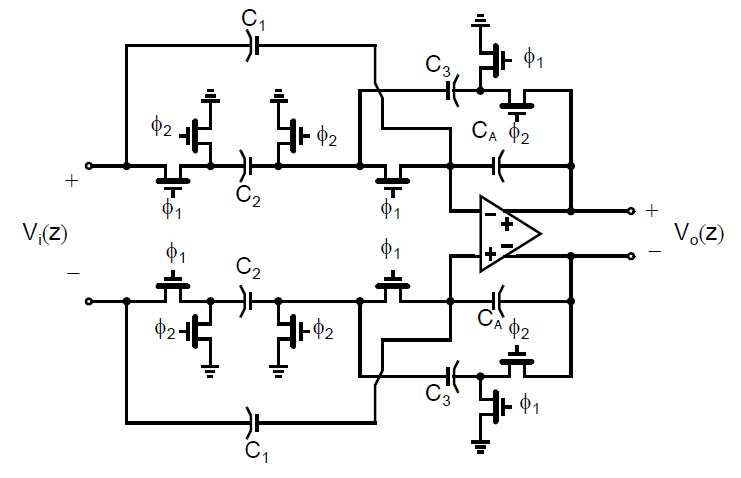
然而，差分电路有着更多的开关和连线，所以最后电路面积还是会比单端电路更大，尽管良好的设计可以使得其面积显著小于两倍单端的面积。此外，全差分电路有着更好的共模噪声抑制性能和更好的抗失真性能。