模拟集成电路设计系列博客——5.1.2 开关电容电路的分析
5.1.2 开关电容电路的分析
考虑如下图(a)所示的开关电容电路,其中\(V_1\)和\(V_2\)是两个直流电压源。

为了分析电路的行为,我们从电荷的角度来分析电路。我们知道电容上的电荷\(Q_x\)等于电容容值\(C_x\)乘以电容两端电压\(V_x\),在数学上,我们有:
现在假定\(\phi_1\)和\(\phi_2\)为一对不交叠时钟,\(C_1\)分别在每个时钟周期充电到\(V_1\)和\(V_2\),因此一个时钟周期上发生的从节点\(V_1\)传输到节点\(V_2\)的电荷变化\(\Delta Q_1\)为:
由于电荷传输每个时钟周期都会发生,我们可以根据传输的电荷量除以时钟周期得到等效平均电流,换而言之,平均电流\(I_{avg}\)(在放大器中)等于:
其中\(T\)为时钟周期,采样频率\(f_s=1/T\)。将\((5.1.3)\)和一个等效电阻的电路进行对比,如上图中(b)所示,有:
我们可以看到(a)中的开关电容电路流经的平均电流与(b)中的电阻流经的电流在满足下式时相等:
这个公式的成立很容易理解,当时钟频率增加时,相同的电荷量仍然在每个时钟周期内传输,但是速率变得更快,因此平均电流更大。如果\(C_1\)增大,那么每个时钟周期要传输的电荷量也更大,因此会增大平均电流。此外,增大平均电流等效于减小两个电压节点之间的等效电阻,因此等效电阻与电容以及时钟频率成反比。
最后,需要注意的是电阻近似假定了每个时钟周期传输的电荷量是固定的,因此其对于分析开关电容电路的低频行为是有用的,即电压变化相比于时钟频率低很多的情况。对于较高的输入频率(与采样频率有关),需要进行精确的离散时间分析。之后会进行讨论。之所以能在开关电容电路中应用离散时间分析,是因为电荷的传输依赖于特定时间的节点电压值,而与非采样时间的瞬态无关。
例题1. 对于一个\(5pF\)电容在时钟频率\(100KHz\)采样时等效电阻是多少?
解答:
根据\((5.1.5)\),我们有:
这意味着通过两个晶体管,一个时钟和一个很小的电容就可以实现一个很大的\(2M\Omega\)的阻抗。一般这么大的阻抗需要一块很大的CMOS硅面积来实现,如果没有任何特殊的工艺生产步骤的话。
首个实现开关电容离散时间积分器的例子如下图所示[Hosticka,1997]:
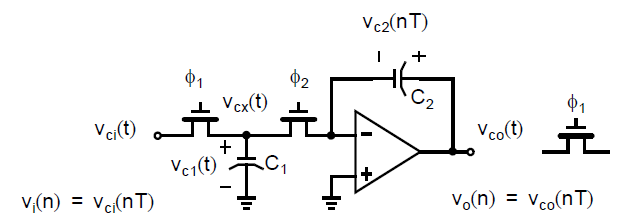
此处,一个额外的开关出现在输出节点\(v_{co}(t)\)旁边,意思是输出信号在\(\phi_1\)结束时有效,换而言之,任何使用这个离散时间积分器的输出的电路,应该在\(\phi_1\)结束时采样\(v_{co}(t)\)。注意虽然我们没有对\(v_{ci}(t)\)的值何时改变做出假设(可以是\(\phi_1\)或是\(\phi_2\)),但这并不重要,因为\(v_{ci}(t)\)仅在\(\phi_1\)结束时被采样。
为了分析这个电路,我们再次查看电荷行为,并且注意到放大器的负极有一个虚地点。假定初始放大器输出电压为\(v_{co}(nT-T)\),这意味\((nT-T)\)时刻\(C_2\)上的电荷为\(C_2v_{co}(nT-T)\)。同样是在\((nT-T)\),\(\phi_1\)刚刚关断(\(\phi_2\)是关断的)因此输入信号\(v_{ci}(t)\)已被采样,使得\(C_1\)上的电荷等于\(C_1v_{ci}(nT-T)\)。如下图(a)所示,当\(\phi_2\)升高时,会强制使得\(C_1\)放电,因为在\(C_1\)的顶极板连接了虚地点,如图(b)所示。
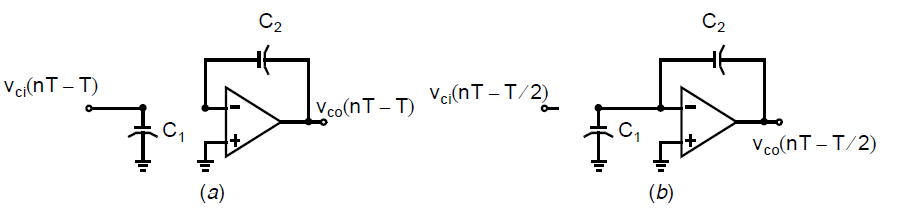
然而,放电电流必须流经\(C_2\),因此\(C_1\)上的电荷增加到\(C_2\)已有的电荷上。注意到正的输入电压会导致\(C_2\)两端产生负的电压,使得输出电压也为负,因此这个积分器是一个反相积分器。在\(\phi_2\)结束时,我们可以写出电荷方程:
\((5.1.7)\)中的负号表示积分器是反相积分器。
尽管\((5.1.7)\)是正确的,但是我们更想找出\(C_2\)在\(\phi_1\)结束时(或者说\(nT\))的电荷。因为\(v_{co}(t)\)是在\(\phi_1\)结束时采样的,为了求得这个电荷值,我们注意到一旦\(\phi_2\)关断,\(C_2\)的电荷在下一个\(\phi_1\)保持相等,直到下一个周期的\(\phi_2\)再次打开。因此,\(C_2\)上的电荷在时刻\((nT)\),即下一个\(\phi_1\)时,等于时刻\((nT-T/2)\)时的电荷。因此有:
我们结合\((5.1.7)\)和\((5.1.8)\)可以得到:
等式两边同时除以\(C_2\),并假定离散时间变量\(v_i(n)=v_{ci}(nT)\),\(v_o(n)=v_{co}(nT)\),我们有如下的离散时间表达式:
对这个公式两边做Z变换,有:
因此我们可以得到最终的传输函数\(H(z)\)为:
注意到这个传输函数通过两个电容的比值来实现增益因子,因此传输函数可以在集成电路中精确实现。一般来说,这个传输函数会抵消掉\(z\)的负幂次项,重写为:
这个离散时间积分器的典型波形如下图所示:
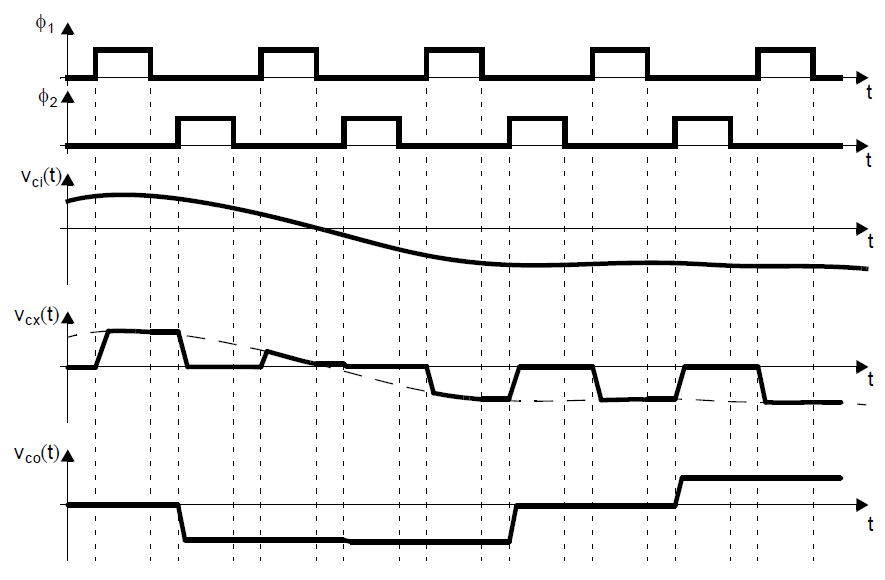
注意这里离散时间方程仅仅表示了\((nT)\)时刻的电压信号\(v_{ci}(t)\)和\(v_{co}(t)\),这只在\(\phi_1\)结束时出现。这并没有给出其他时刻的电压值,事实上,这些电压在其他时刻保持固定(忽略所有的二阶效应),这等效于取采样电压然后将其作为这个开关电容积分器的采样保持的输入。
例题2:
假定输入信号频率远低于采样频率,将公式\((5.1.12)\)近似为一个理想连续时间滤波器。
解答:
\((5.1.12)\)可以重写为:
为了求得频率响应,我们需要使用:
其中\(T\),其等于采样频率的倒数,因此:
以及:
将\((5.1.16)\)和\((5.1.17)\)代入\((5.1.14)\)中有:
对于\(\omega T <<1\),分子的\(z^{-1/2}\)表示一个简单的延迟,并且可以忽略。因此,我们可以看到传输函数近似为一个连续时间滤波器,其增益常数为:
这个常数是一个积分器电容比例以及时钟频率的函数。
到目前为止我们忽略了\(C_1\)和\(C_2\)制造时的寄生电容的影响以及开关相关的非线性电容。增加这些电容会得到如下图所示的电路:
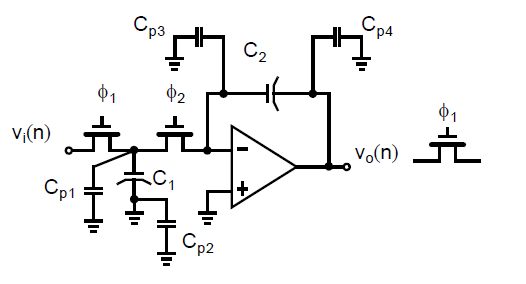
此处,\(C_{p1}\)表示\(C_1\)顶极板的寄生电容以及两个开关的非线性电容,\(C_{p2}\)表示\(C_1\)底极板的寄生电容,\(C_{p3}\)表示\(C_2\)顶极板的寄生电容以及放大器的输入电容和\(\phi_2\)开关的电容,\(C_{p4}\)表示\(C_2\)底极板的寄生电容以及放大器必须驱动的额外电容。
考虑了这些寄生电容之后,我们可以立刻忽略掉\(C_{p2}\)的影响,因为它一直接地。类似的,\(C_{p3}\)对于传输函数的影响很小,因为它一直连接放大器的虚地点。此外,\(C_{p4}\)连接再放大器的输出,因此,尽管它可能会影响放大器的速度,但是它不会影响放大器输出的最终建立点。最后,我们注意到\(C_{p1}\)和\(C_1\)并联,因此考虑到寄生效应后的离散时间积分器的传输函数为:
从\((5.1.20)\)中可以看出,增益因子与寄生因子\(C_{p1}\)有关,这并不好控制,并且由于开关和顶极板的寄生电容存在部分的非线性。为了克服这个缺陷,后续电路研究了对寄生不敏感的结构[Martin,1978; Allstot,1978; Jacobs,1978]。
寄生不敏感的积分器是一个重大的突破,使得高精度集成电路的实现成为可能。在第一个基于集成积分器的滤波器中,下图所示的正相积分器是寄生参数不敏感的[Allstot,1978],但反相积分器是寄生参数敏感的。
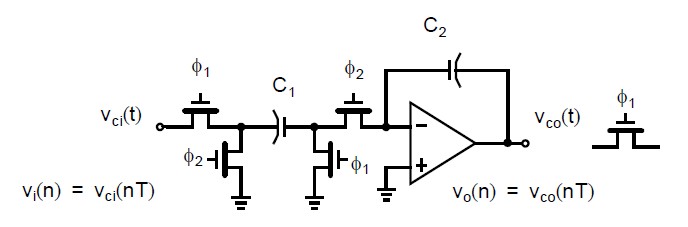
但后续发展的寄生不敏感反相积分器[Martin,1978; Jacobs,1978]使得整个滤波器都可以寄生不敏感,显著降低了二阶效应误差。为了实现寄生不敏感离散时间滤波器,上图中使用了两个额外的开关。对这个电路运用之前的分析方法,我们注意到但\(\phi_1\)打开时,\(C_1\)充电到\(C_1v_{ci}(nT-T)\),如下图(a)所示,当\(\phi_2\)打开时,\(C_1\)被反过来,放电出现在地节点而不是输入信号一侧,如下图(b)所示。
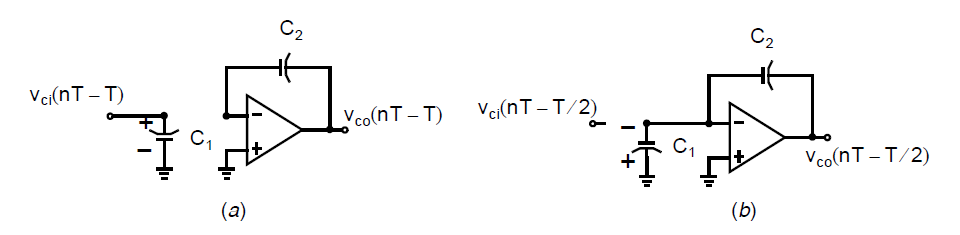
这个反相连接使得\(v_{co}(t)\)上升到了正的\(v_{ci}(nT-T)\),因此积分器是正相的。通过之前的分析,我们可以得到这个离散积分器的传输函数:
注意到上式表示正相离散积分器,并带有一个从输入到输出的延迟(分子的\(z^{-1}\)表示一个周期的延迟)所以上面的电路表示延迟离散时间积分器。和我们之前对反相积分器做的类似,可以将这个传输函数重写来消除\(z\)的负幂次项:
为了观察带有寄生电容的正相积分器的行为,考虑带有寄生电容的这个电路,如下图所示:
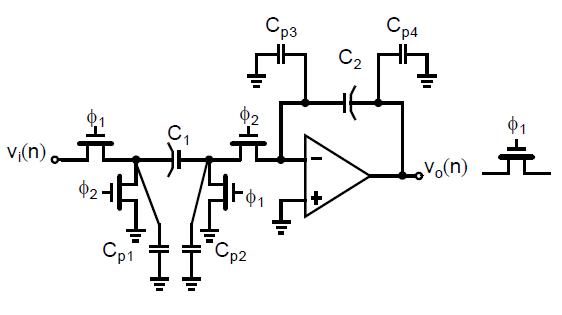
此处,\(C_{p3}\)和\(C_{p4}\)响电路的工作,就如之前分析反相积分器那样。此外\(C_{p2}\)也通过\(\phi_1\)连接到地或者通过\(\phi_2\)连接到虚地点。因此,由于\(C_{p2}\)始终保持放电(在建立之后),它不会影响电路的工作。最后,\(C_{p1}\)持续被充电到\(v_i(n)\)和放电到地。当\(\phi_1\)打开时,\(C_{p1}\)被充电到\(v_i(n-1)\)并不会影响\(C_1\)上的电荷。当\(\phi_2\)打开,\(C_{p1}\)通过连接到其节点的\(\phi_2\)放电,并且其放电电流不会流经\(C_1\)去影响\(C_2\)上积累的电荷。因此,它也不会影响电路的工作。总而言之,尽管寄生电容可能会减慢建立时间行为,它们不会影响电路的离散时间差分方程。
为了得到寄生参数不敏感的反相离散时间积分器,可以使用与正相离散时间滤波器同样的电路结构只是将靠近放大器输入侧和\(C_1\)(即\(C_1\)顶极板)的开关相位进行交换,如下图所示[Martin,1978]:
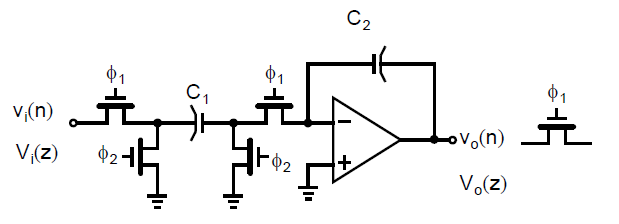
这样安排电路之后,注意\(\phi_2\)打开时\(C_2\)上的电荷保持不变(此时\(\phi_1\)关断),如下图(b)所示:
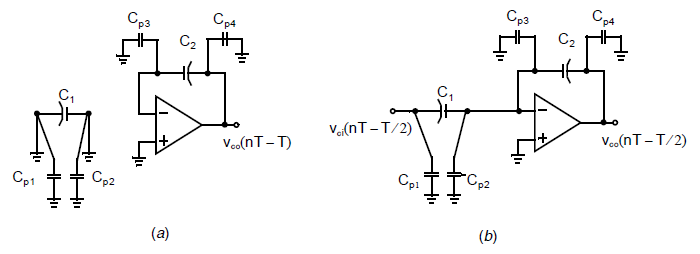
因此,我们可以写出:
同样注意\(C_1\)在\(\phi_2\)打开结束时完全放电。注意此时\(\phi_1\)如上图(a)所示已经打开,\(C_1\)被充电到\(v_{ci}(t)\)。然而,电流需要通过\(C_2\)给\(C_1\)充电,导致对应的改变\(C_2\)上相等数额的电荷。在\(\phi_1\)打开结束时,\(C_2\)上留存的电荷,等于其旧的电荷(\(\phi_1\)打开之前)减去其需要将\(C_1\)充电到\(v_{ci}(nT)\)的电荷,我们得到如下公式:
注意这里方程内的是\(v_{ci}(nT)\)而不是\(v_{ci}(nT-T)\),因为\(C_2\)在\(\phi_1\)结束时的电荷同时是与\(v_{ci}(nT)\)相关的,因此积分器可以被认为是无延迟的。结合\((5.1.23)\)和\((5.1.24)\),并在等式两边同时除以\(C_2\)可以得到:
对两边做\(z\)变换后,得到该无延迟积分器的传输函数为:
分子项是一个纯实数项表示这个积分器是无延迟的,\((5.1.26)\)一般写成如下的形式:
最后,注意到无延迟积分器的增益为负,而又延迟积分器增益为正。这些增益上的符号变化在单端开关电容电路中可能很有用,大部分现代集成电路使用全差分信号来提升噪声表现,并可以通过简单的交叉输出线来实现符号变化。因此,上面介绍的两个电路都可以通过全差分来实现,并取得正或负的增益。因此最好用延迟积分器和无延迟积分器来区分这两者。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号