模拟集成电路设计系列博客——5.1.1 开关电容电路基本模块

5.1.1 开关电容电路基本模块

开关电容电路由如放大器，电容，开关和不交叠时钟这些基本模块组成。接下来我们将简单介绍这些模块，以及它们在开关电容电路中使用时存在的非理想性。

如果在开关电容电路中使用理想放大器的话，那么电路的原理会很容易理解。然而实际放大器的一些非理想性在开关电容电路中使用时会造成影响，这些非理想性包括了直流增益，单位增益频率与相位裕度，摆率以及直流失调电压。放大器的输入阻抗一般为容性，假定使用MOSFET输入级的话。

用于开关电容电路中的MOS工艺的放大器直流增益一般在40到80dB。低的直流增益会影响一个开关电容滤波器的离散时间传输函数的因子的准确性。

放大器的单位增益频率与相位裕度决定了其小信号建立行为。一般来说开关电容电路的时钟频率应该比放大器的单位增益频率低五倍，这样几乎不会出线压摆率行为，并且相位裕度大于70度。现代开关电容电路一般使用有着大输出阻抗（\(100k\Omega\)甚至更大）的高频率单级放大器。由于这些放大器的负载是纯容性（完全没有阻性），他们的直流增益尽管没有输出缓冲级也仍然很大。需要注意的是他们的单位增益频率和相位裕度是收到负载电容决定的，其同样也作为补偿电容。因此，在这些单级放大器中，将负载电容增大两倍会将单位增益频率减少一半，并提升相位裕度。

放大器的有限摆率会限制开关电容电路中的上升时钟速率，因为这些电路依靠快速将电容从一个电容转移到另一个电容。因此，在进行电荷传输时，放大器收到摆率限制的情况并不少见。

根据电路所选择的工艺，非零直流失调可能会导致一个很高的输出直流失调。幸运的是，一个被称为相关双采样的技术可以显著减少输出失调，同时降低低频放大器输入噪声（例如1/f噪声）。

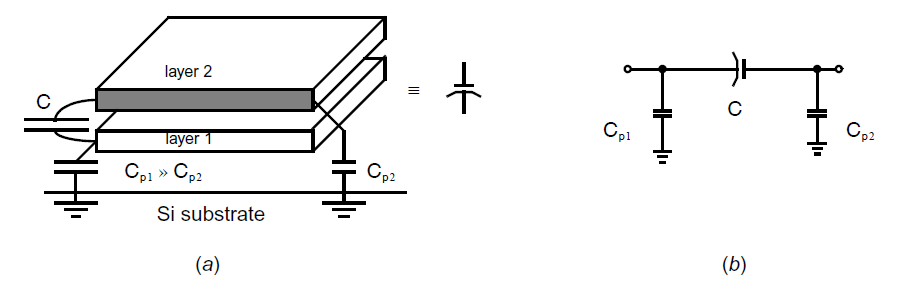
在集成电路中，一个高度线性化的电容一半通过两个紧密摆放的导体层来实现，如下图中的(a)所示，电容\(C\)通过两个导体层1和层2之间的交叠区来实现。

尽管层下的衬底是交流地（衬底连接一个电源，或者模拟地），仍然会存在寄生电容\(C_{p1}\)，其大小大概是\(C\)的百分之20。这个大寄生电容\(C_{p1}\)被称为底板电容。此外顶极板电容\(C_{p2}\)由于电容的互联而存在，但它一般会小很多（大概只有\(C\)的百分之五）。总之，一个单独的集成电容的等效模型由三个电容组成，如上图中的(b)中所示。其中底极板一般会清晰标出来（通过图中的半弧线）表示这个节点上有一个更大的寄生电容。

开关电容电路中的开关需要有一个非常大的关断阻抗（使得电荷泄露很小），和一个相对小的开态电阻（从而使得电路可以在一半时钟周期内完成建立），并且在打开时不会引入失调电压。使用MOSFET晶体管作为开关可以满足上述要求，由于MOSFET开关在关断时可以达到\(G\Omega\)量级的电阻，没有开态失调电压，开态电阻小于\(5k\Omega\)甚至更小，取决于晶体管尺寸。

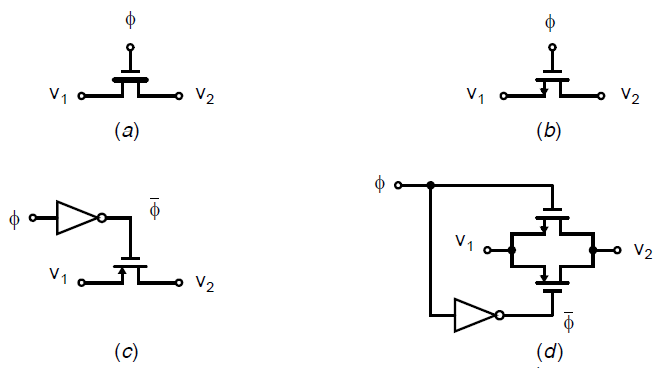
开关的符号以及一些开关的MOSFET电路实现如下图所示：

这里信号\(\phi\)是等于最大或者最小电源的电平值，一般来说，当时钟信号\(\phi\)为高时，开关打开（短路）。尽管开关可以使用单个晶体管实现，如上图中的(a)和(b)所示，但是这样开关的信号范围就会受限。例如，考虑如(b)的理想n沟道晶体管开关应用在电源为\(0V\)和\(1.8V\)的电路中，阈值电压\(V_{tn}=0.45\)，那么当栅压为\(0V\)时开关保持关断，无论输入电压为多少。但是，当开关打开是，其栅压稳定为\(V_{DD}=1.8V\)，在这种情况下，只有当电压\(V_1\)和/或\(V_2\)低于\(V_{DD}-V_{tn}\)时才能工作，如果再考虑体效应，那么大约在\(1.3V\)，因此这个开关的信号范围被限制在\(0V\)到\(1.3V\)。类似的论断对于(c)中的p沟道晶体管同样成立，其信号范围会被限制在\(0.5V\)到\(1.8V\)。尽管这种受限的信号幅度在某些情况下也是可以接受的，但是使用两个并联的晶体管可以实现\(0V\)到\(1.8V\)的完整信号范围，如(d)所示。这个电路一般被称为CMOS开关（与(a)中的NMOS开关相对），或者叫做一个CMOS传输门。

一些严重影响开关电容电路的非理想开关效应包括开关两侧的非线性结电容，沟道电荷注入，以及逻辑信号\(\phi\)到开关两侧的电容耦合。使用非寄生敏感结构可以降低非线性电容影响，通过精心设计开关时序可以降低沟道电荷注入。

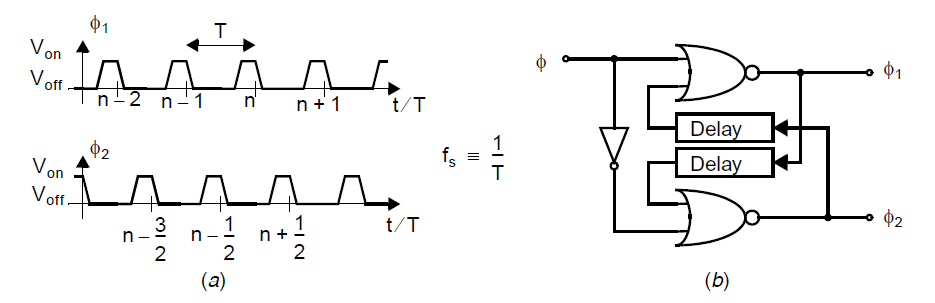
开关电容中至少需要一对不交叠时钟。这些时钟决定了何时电荷开始传输，并且它们必须不交叠来确保电荷不会意外丢失。如下图(a)所示，所谓不交叠时钟指的是两个同频的逻辑信号通过调整使得两个信号不会同时为高。注意(a)中的横轴被归一化到时钟周期\(T\)。通过归一化表示开关电容电路中离散时间信号的采样次数。一般来说，我们将\(\phi_1\)的采样次数表示为整数（例如\((n-1)\)，\(n\)，\((n+1)\)等），计数发生在每个时钟相位\(\phi_1\)结束之前，而在每个时钟相位\(\phi_2\)结束之前，我们计其为\(\phi_1\)整数值偏移\(1/2\)（例如\((n-3/2)\)，\((n-1/2)\)等），需要注意的是\(\phi_2\)的下降时间沿一半提前\(\phi_1\)下降时间沿半个时钟周期。总体来说，\(\phi_1\)和\(\phi_2\)的时间沿需要精确控制以实现完整的电荷建立（假定整个电路使用独立低抖动的采样和保持）。

一种简单的实现不交叠时钟的方式如上图(b)所示[Martin,1981]。此处通过延迟单元来确保时钟保持不交叠。延迟单元通过堆叠偶数个反相器或者一个\(RC\)网络来实现。