模拟集成电路设计系列博客——4.4.4 Q因子修调

4.4.4 Q因子修调

在一些需要高速或者高度选择的滤波器中，非理想的积分器效应和寄生参数使得电路需要对积分器的极点进行Q因子修调。尽管我们之前讨论过如何通过修调单独的时间常数使得集成滤波器的的因子达到百分之1以内的误差，当\(Q>1\)时，即使Q因子上有微小的误差也可能会在滤波器频率和阶跃效应上产生大的误差。因此，在一些应用中需要额外的修调来精确设置Q因子。

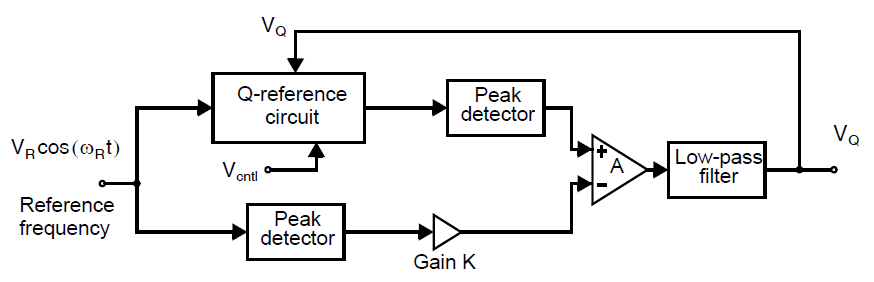
一种进行Q因子修调的方式是修调滤波器积分器的相位来确保其相对于滤波器的通带边缘有着90度的相位滞后。积分器的相位响应可以通过引入可调电阻（通过一个线性区晶体管来实现）与积分电容串联来调整。对这个可调电阻的控制电压\(V_Q\)通过一个Q因子修调电路来产生，如下图所示，并将控制信号传输给所有的滤波器积分器。

另外，当积分器滤波器为二阶时，极点\(Q\)可以通过改变滤波器中的阻尼跨导器的跨导来调整。具体来说，考虑到\((4.4.4)\)中的分母，我们将其重写为通过\(\omega_o\)和\(Q\)表示的形式，我们有：

\[s^2+s(k_{m3}/k_{XB})(G_{m1}/C_A)+(k_{m1}k_{m2}/k_{XB})(G_{m1}/C_A)^2 = s^2+s(\frac{\omega_0}{Q}+\omega_o^2) \tag{4.4.7} \]

求解这个方程，我们可以得到如下关系式：

\[\omega_o=(\frac{G_{m1}}{C_A}\sqrt{\frac{k_{m1}k_{m2}}{k_{XB}}}) \tag{4.4.8} \]

\[Q=(\frac{k_{XB}}{k_{m3}})\sqrt{\frac{k_{m1}k_{m2}}{k_{XB}}} \tag{4.4.9} \]

从\(Q\)的表达式中，我们可以看出滤波器极点的Q因子与\(k_{m3}\)呈反比，因此我们只需要调整\(G_{m3}\)就可以调整二阶滤波器的Q因子。

控制信号\(V_Q\)对于任意的Q因子调节方法，都可以用上图中采用的幅度锁定环路系统来实现[Schaumann,1990]。这个电路的工作是基于Q因子的误差会使得滤波器的频率响应出现幅度误差。为了测量幅度误差，一个合适参考频率的正弦信号被施加到Q参考电路上，其输出的幅度与输入信号缩放之后的幅度进行比较。正弦频率可以通过频率修调电路中的VCO的输出来获得。