模拟集成电路设计系列博客——4.2.2 线性区晶体管跨导器

4.2.2 线性区晶体管跨导器

本节我们将讨论使用工作在线性区的晶体管构成的跨导器。需要说明的是，在下面介绍的电路中，并不是所有的晶体管都处于先行区。一些晶体管被偏置在饱和区，但是电路的跨导由一到两个被偏置在线性区的关键晶体管来决定。

首先我们会议一下对于n管来说线性区的电流公式：

\[I_D=\mu_nC_{ox}(\frac{W}{L})[(V_{GS}-V_{th})V_{DS}-\frac{V_{DS}^2}{2}] \tag{4.2.6} \]

以及处于线性区的条件：

\[V_{DS}<V_{eff}(V_{eff}=V_{GS}-V_{th}) \tag{4.2.7} \]

在上述方程式准确的情况下，我们可以实现完美的线性电路。然而在现代短沟道工艺中，这些方程并不是非常精确。因此在实际电路中会由于高阶项而产生一些失真。在实际的连续时间电路中使用全差分结构来消除偶次失真项，剩下的三阶失真项成为主导。

从\((4.2.6)\)中我们可以看出，如果使用的是小信号\(V_{DS}\)，那么\(V_{DS}^2\)项将很接近于零，漏极电流大约近似于源漏电压成线性关系。我们可以建模一个线性区晶体管为一个电阻：

\[r_{DS}=(\frac{\partial I_{D}}{\partial V_{DS}})^{-1}|_{V_{DS}=0} \tag{4.2.8} \]

从而可以求出小信号电阻为：

\[r_{DS}=\frac{1}{\mu_nC_{ox}(\frac{W}{L})(V_{GS}-V_{th})} \tag{4.2.9} \]

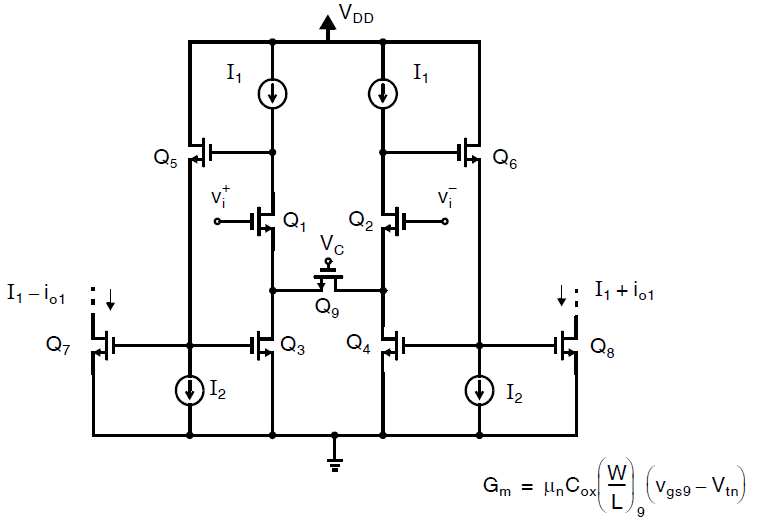
下图展示了一种电路的实现方案[Welland,1994]，除了晶体管\(Q_9\)被偏置在线性区，其他的晶体管都处于饱和区。由于\(Q_1\)和\(Q_2\)上流经的电流固定，他们各自的栅源电压也是固定的，因此电路的跨导就等于\(Q_9\)小信号电阻\(r_{ds}\)的倒数。使用\((4.2.9)\)的公式我们可以知道这个电路的跨导为：

\[G_m=\frac{i_{o1}}{v_i^{+}-v_i^{-}}=\mu_nC_{ox}(\frac{W}{L})_9(V_{gs9}-V_{th}) \tag{4.2.10} \]

因此这个跨导器可以通过改变\(V_{gs9}\)的值来调整跨导。此外调整电流镜晶体管\(Q_3\)，\(Q_4\)和\(Q_7\)，\(Q_8\)的尺寸也可以缩放跨导。\(Q_5\)和\(Q_6\)作为源极跟随器而工作，当\(Q_3\)和\(Q_4\)的\(V_{DS}\)被拉低时，\(Q_5\)和\(Q_6\)能够相应的拉低\(Q_3\)和\(Q_4\)的\(V_{GS}\)使得他们保持在饱和区下。

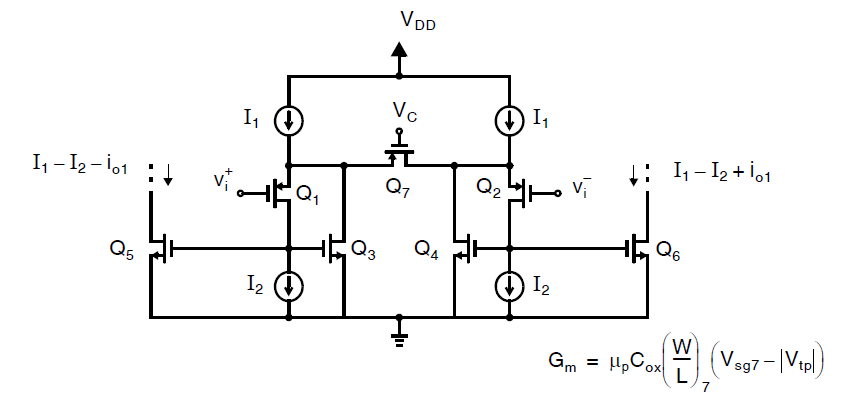
这张图里展示了一种与上图原理类似，但是复杂度更低的p沟道晶体管作为输入的方案[Kwan,1991]。恒定电流\(I_2\)流经\(Q_1\)和\(Q_2\)，\(Q_3\)和\(Q_4\)的偏置电流等于\(I_1\)与\(I_2\)之差，信号电流\(i_{o1}\)通用流经\(Q_3\)和\(Q_4\)并被镜像到输出晶体管\(Q_5\)和\(Q_6\)上，注意这样的拓扑使得输入晶体管环路上可以省去上图中的\(Q_5\)和\(Q_6\)的源极跟随器。使得这个电路相对于上面的电路可以有速度上的优势。

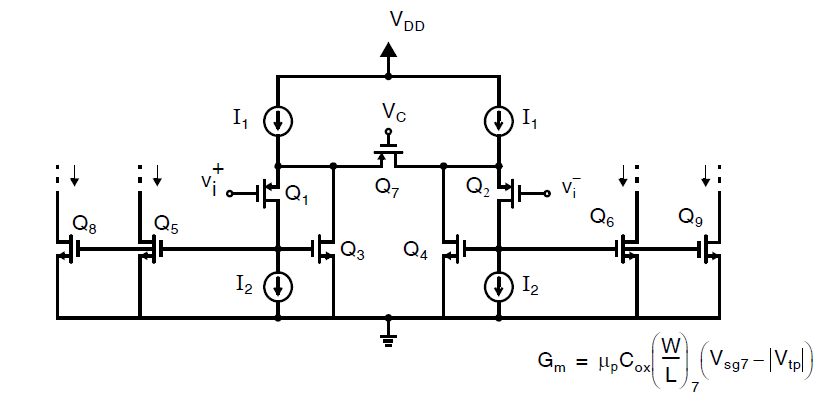
上面介绍的两种电路有一个共同的优势，就是他们可以通过引入额外的输出晶体管可以很简单的获得多个输出。例如，下图展示了上图电路增加到两路输出的情况。这些额外的晶体管可以缩放到任意想要的比例来缩放输出电流。

这种多路输出能力使得滤波器可以使用更少的晶体管实现。比如在之前介绍过的二阶滤波器中，使用多路输出跨导器，可以节省掉两个跨导器，这样做不仅可以节省面积，更重要的是可以节省功耗。

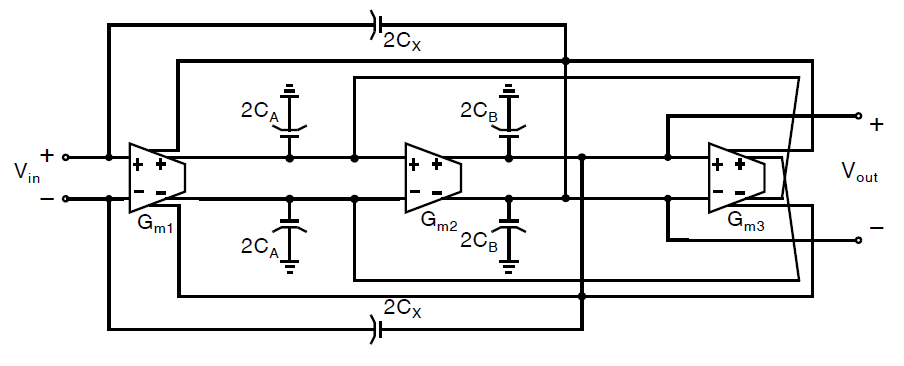
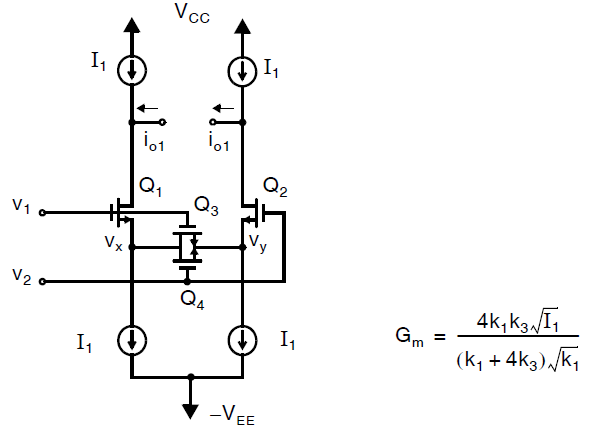
另一种使用线性区晶体管线性化MOSFET差分对的方法如下图所示[Krummenacher,1998]：

注意此处晶体管\(Q_3\)和\(Q_4\)的栅极连接到差分输入电压而不是偏置电压上。作为结果，线性区晶体管\(Q_3\)和\(Q_4\)通过不同的偏置条件来提升这个电路的线性度。为了理解\(Q_3\)和\(Q_4\)如何处于线性区，我们首先假定输入信号相等\((v_1=v_2)\)，从而：

\[v_x=v_y=v_1-v_{GS1}=v_1-(v_{eff1}+V_{tn}) \tag{4.2.11} \]

因此，\(Q_3\)和\(Q_4\)的漏源电压均为零。然而，他们的栅源电压等于\(Q_1\)和\(Q_2\)，因此他们会处于线性区。

为了确定这个电路的小信号跨导，我们首先写出\(Q_3\)和\(Q_4\)的小信号漏源电阻：

\[r_{ds3}=r_{ds4}=\frac{1}{2k_3(V_{GS1}-V_{tn})} \tag{4.2.12} \]

我们假定\(Q_3\)和\(Q_4\)匹配，从而有：

\[k_3=\frac{\mu_nC_{ox}}{2}(\frac{W}{L})_3 \tag{4.2.13} \]

注意到这个电路中我们不能忽视\(Q_1\)和\(Q_2\)栅源电压的变化，因为他们的漏极电流并不是一个常数值。\(Q_1\)和\(Q_2\)的小信号源电阻可以写为：

\[r_{s1}=r_{s2}=\frac{1}{g_{m1}}=\frac{1}{2k_1(V_{GS1}-V_{tn})} \tag{4.2.14} \]

使用小信号T模型，我们可以求出小信号输出电流\(i_{o1}\)为：

\[i_{o1}=\frac{v_1-v_2}{r_{s1}+r_{s2}+(r_{ds3}||r_{ds4})} \tag{4.2.15} \]

因此，定义\(G_m=i_{o1}/(v_1-v_2)\)，我们有：

\[G_m=\frac{1}{r_{s1}+r_{s2}+(r_{ds3}||r_{ds4})} \tag{4.2.16} \]

可以进一步转化为：

\[G_m=\frac{4k_1k_3(V_{GS1}-V_{tn})}{k_1+4k_3} \tag{4.2.17} \]

考虑到电流\(I_1\)有：

\[I_1=k_1(V_{GS1}-V_{tn})^2 \tag{4.2.18} \]

因此：

\[V_{GS1}-V{tn}=\sqrt{\frac{I_1}{k_1}} \tag{4.2.19} \]

从而：

\[G_m=\frac{4k_1k_3\sqrt{I_1}}{(k_1+4k_3)\sqrt{k_1}} \tag{4.2.20} \]

我们可以看出跨导器的跨导可以通过改变偏置电流\(I_1\)来调整。为了理解线性区晶体管在不同的偏置条件下如何改进电路的线性度，考虑\(v_1\)和\(v_2\)输入小信号（比如\(100mV\)）的情况，在输入小信号时，\(Q_3\)和\(Q_4\)基本上工作于类似两个源极退化电阻。因此线性度相比普通差分对得到了提升（假定\(r_{ds3}>>r_{s1}\)）因为线性区晶体管相比有源区晶体管的源极电阻有着更好的线性度。