模拟集成电路设计系列博客——4.1.3 一阶Gm-C滤波器

4.1.3 一阶Gm-C滤波器

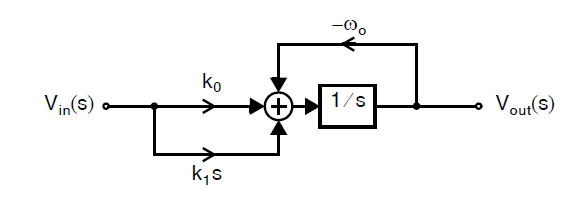
假设我们希望实现如下图所示系统框图的单端\(G_m-C\)滤波器。

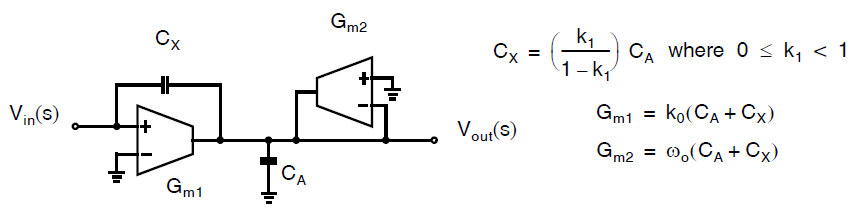
我们可以使用下图所示的电路：

系统框图中的增益通过跨导器来实现，积分通过电容\(C_A\)来实现，而\(C_X\)对应了系统框图中前馈通路\(k_1 s\)。

上面这个一阶\(G_m-C\)滤波器的传输函数可以通过列写一个对于输出节点\(V_{out}(s)\)的电流方程来求得：

\[G_{m1}V_{in}(s)+sC_X[V_{in}(s)-V_{out}(s)]-sC_AV_{out}(s)-G_{m2}V_{out}(s)=0 \tag{4.1.9} \]

变形得到\(V_{out}(s)/V_{in}(s)\)，我们有：

\[\frac{V_{out}(s)}{V_{in}(s)}=\frac{sC_X+G_{m1}}{s(C_A+C_X)+G_{m2}}=\frac{[sC_X/(C_A+C_X)+G_{m1}/(C_A+C_X)]}{s+G_{m2}/(C_A+C_X)} \tag{4.1.10} \]

我们考虑系统框图对应的传输函数：

\[H(s)=\frac{V_{out}(s)}{V_{in}(s)}=\frac{k_1s+k_0}{s+\omega_0} \tag{4.1.11} \]

通过对比\((4.1.10)\)和\((4.1.11)\)，我们可以得到：

\[C_X=\frac{k_1}{1-k_1}C_A \tag{4.1.12} \]

\[G_{m1}=k_0(C_A+C_X) \tag{4.1.13} \]

\[G_{m2}= \omega_0(C_{A}+C_{X}) \tag{4.1.14} \]

需要注意的是，根据\((4.1.12)\)，\(C_X\)必然是一个正数，那么\(k_1\)就必须满足\(0\leq k_1 < 1\)。这就限制了无法实现一个高频增益为负数或者大于1的滤波器（这是因为从\((4.1.11)\)可以很容易得出这个传输函数对应的高频增益为\(k_1\)）。

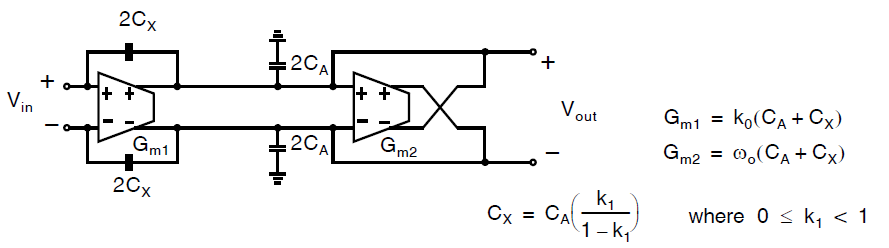
最后，与之等效的全差分一阶\(G_m-C\)滤波器的结构如下图所示，需要注意相比单端情况，这里电容放大了两倍，从而使得相同的设计方程成立。同时也需要注意对\(k_1\)有着一样的限制，尽管我们其实可以通过交叉耦合电容对\(C_X\)的方式来实现负的\(k_1\)。

例题1：

基于本节中的全差分一阶\(G_m-C\)滤波器结构，确定当我们需要实现一个直流增益为\(0.5\)，极点在\(20MHz\)，零点在\(40MHz\)的滤波器时所需要的器件参数，假定\(C_A=2pF\)。

解答：

对于一个零点在\(40MHz\)，极点在\(20MHz\)的一阶滤波器，我们有：

\[H(s)=\frac{k(s+2\pi\times 40MHz)}{s+2\pi \times 20MHz} \tag{4.1.15} \]

根据低频增益为\(0.5\)，我们可以求出因子\(k=0.5\times20MHz/40MHz=0.25\)，从而：

\[H(s)=\frac{0.25s+2\pi\times 10MHz)}{s+2\pi \times 20MHz} \tag{4.1.16} \]

因此对应到\((4.1.11)\)中，我们有：

\[k_1=0.25 \tag{4.1.17} \]

\[k_0=2\pi \times 10^7 \tag{4.1.18} \]

\[\omega_0=4\pi\times 10^7 \tag{4.1.19} \]

使用设计方程\((4.1.12)\)到\((4.1.14)\)，我们可以得到：

\[C_X=2pF\times \frac{0.25}{1-0.25}=0.667pF \tag{4.1.20} \]

\[G_{m1}=2\pi \times 10^7 \times 2.667pF=0.168mA/V \tag{4.1.21} \]

\[G_{m2}=4\pi \times 10^7\times 2.667pF=0.335mA/V \tag{4.1.22} \]