模拟集成电路设计系列博客——3.4.2 稳压器反馈分析

3.4.2 稳压器反馈分析

上一小节中介绍的稳压器的开环分析与基本源极跟随器很相似，假定使用一个跨导为\(G_{ma}\)，输出阻抗为\(R_{oa}\)的单级放大器，环路在放大器的输入处断开并是呀一个测试信号\(v_{t}\)，可以得到如下图所示的小信号等效电路。稳压器负载通过小信号电阻\(R_L\)建模，并和\(r_{ds1}\)以及\(1/g_{s1}\)并联形成\(R_L^{'}\)。

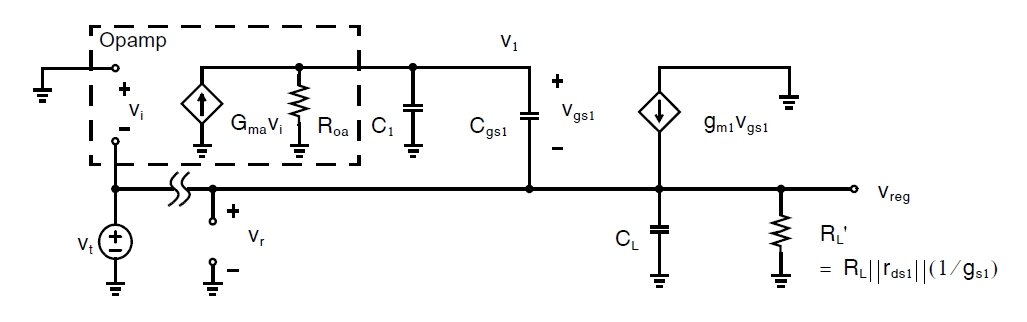
用近似于共漏放大器（源极跟随器）的分析方式我们可以得到开环传函为

\[L(s)=(\frac{G_{ma}R_{oa}R_L^{'}}{R_L^{'}+1/g_{m1}})\frac{(1+sC_{gs1}/g_{m1})}{(1+s/{\omega_0Q}+s^2/\omega_0^2)} \tag{3.4.4} \]

其中：

\[\omega_0=\sqrt{\frac{(1/R_{oa})(g_{m1}+1/R_L^{'})}{C_{gs1}C_L+C_1(C_{gs1}+C_L)}} \tag{3.4.5} \]

\[Q=\frac{\sqrt{(1/R_{oa})(g_{m1}+1/R_L^{'})[C_{gs1}C_L+C_1(C_{gs1}+C_L)]}}{C_L/R_{oa}+C_1(g_{m1}+1/R_{oa})+C_{gs1}/R_L^{'}} \tag{3.4.6} \]

假定环路采取主极点补偿，则\(Q<<1\)，可以将\((3.4.4)\)的分母分成两个一阶项：

\[L(s)=(\frac{G_{ma}R_{oa}R_L^{'}}{R_L^{'}+1/g_{m1}})\frac{(1+s/\omega_{z})}{(1+s/{\omega_{p1}})(1+s/\omega_{p2})} \tag{3.4.7} \]

因此极点为：

\[-\omega_{p1}=-\omega_0Q=-\frac{(1/R_{oa})(g_{m1}+1/R_L^{'})}{C_L/R_{oa}+C_1(g_{m1}+1/R_{oa})+C_{gs1}/R_L^{'}} \tag{3.4.8} \]

\[-\omega_{p2}=-\frac{\omega_0}{Q}=-\frac{C_L/R_{oa}+C_1(g_{m1}+1/R_{oa})+C_{gs1}/R_L^{'}}{C_{gs1}C_L+C_1(C_{gs1}+C_L)} \tag{3.4.9} \]

由于\(C_{gs1}\)的反馈通路，电路被引入了一个零点：

\[-\omega_z=-g_{m1}/C_{gs1} \tag{3.4.10} \]

有两种不同的方式补偿环路，如果\(C_1\)通过在\(V_1\)和地之间增加额外的补偿电容来增大，那么\(C_1g_{m1}\)会成为\((3.4.8)\)分母中的主导项和\((3.4.9)\)中分子的主导项。作为结果，主极点\(\omega_{p1} \approx 1/R_{oa}C_1\)与\(v_1\)处的时间常数有关，\(\omega_{p2}\approx g_{m1}/C_L\)与\(v_{reg}\)的时间常数有关。在这个情况下，仍然需要一个电容加在输出\(C_L\)处来滤除\(v_{reg}\)上的高频噪声。另一种方式时将\(C_L\)设的很大，\(R_{oa}\)减小，那么\(C_L/R_{oa}\)是\((3.4.8)\)和\((3.4.9)\)中的主导项。在这个情况下，这两个极点发生交换，\(\omega_{p1}\)是输出极点而\(\omega_{p2}\)是\(v_1\)处的极点。则需要一个更大的补偿电容，以及更高的放大器功耗，但在输出处提供了一个大的电容从而提高了电源抑制比以及降低中高频上的阻抗。总体来说，零点\(\omega_z\)会处在一个远高于极点的频率，并对稳定性的影响微乎其微。