模拟集成电路设计系列博客——3.3.2 带隙电压基准电路

3.3.2 带隙电压基准电路

带隙电压基准可以分为双极型晶体管实现方案和CMOS晶体管实现方案，由于目前更常用的是CMOS工艺，因此这里略去双极型工艺下的带隙电压基准方案的描述，主要讨论CMOS方案。尽管是使用CMOS工艺，但带隙电压基准的原理要求其仍然得要使用双极型晶体管，所以必须使用一个CMOS工艺兼容的方式将其进行实现。

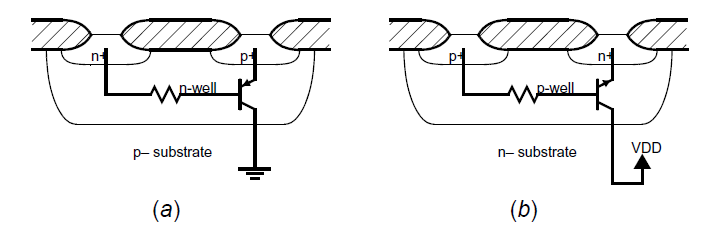
最流行的实现CMOS电压基准的方案仍然是带隙电压基准，尽管没有办法实现独立的双极型晶体管。但是CMOS电路可以依靠我们称为阱电阻的器件实现双极型晶体管，这些器件垂直方向上构成了双极型晶体管，以阱作为其基极，以衬底作为其集极。如下图（a）所示，在一个n阱工艺中，这些垂直双极型晶体管是pnp型的，集极连接到地。如下图（b）所示，在p阱工艺中，垂直双极型晶体管会是npn型的，集极连接到正电源电压。

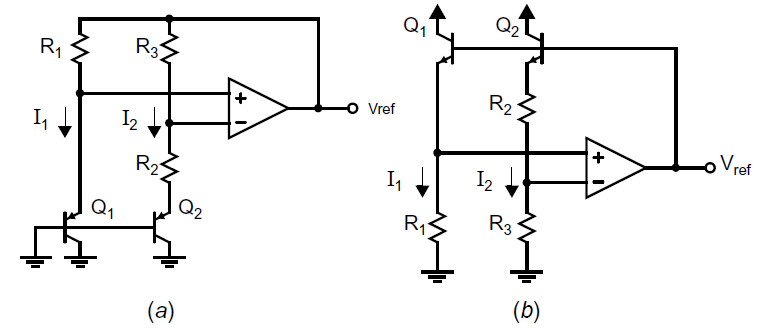
这些晶体管有着可观的电流增益，但是其主要限制是，因为基极触点和有效射极区之间的大横向尺寸，串联基极电阻可能会很大。为了减小由于基极电阻带来的误差，流经晶体管的最大集极电流一般被限制在小于\(0.1mA\)。可以使用这些晶体管来实现带隙电压基准，在n阱工艺下可以使用下图中（a）的结构[Kujik, 1973]，在p阱工艺下可以使用下图中（b）的结构[Ye, 1982]。

对于（a）中的n阱方案，我们有：

\[V_{ref}=V_{EB1}+V_{R1} \tag{3.3.18} \]

假定放大器有着大增益，并且其输入端有着相同的电压，那么：

\[V_{R2}=V_{EB1}-V_{EB2}=\Delta V_{EB} \tag{3.3.19} \]

现在，由于流经\(R_3\)的电流和流经\(R_2\)的电流相等，我们有：

\[V_{R3}=\frac{R_3}{R_2}V_{R2}=\frac{R_3}{R_2}\Delta V_{EB} \tag{3.3.20} \]

根据\((3.3.19)\)，放大器反馈使得\(R_1\)两端的电压等于\(R_3\)两端的电压，据此将\((3.3.20)\)代入\((3.3.18)\)后有：

\[V_{ref}=V_{EB1}+\frac{R_3}{R_2}\Delta V_{EB} \tag{3.3.21} \]

从上一小节中我们知道这就是实现带隙电压基准需要的形式。在基准的具体实现中，双极型晶体管一般使用相同的尺寸，不同的电流密度通过将\(R_3\)取得大于\(R_1\)来实现，从而使得\(I_1\)大于\(I_2\)，在这个例子中，我们有：

\[\frac{J_1}{J_2}=\frac{R_3}{R_1} \tag{3.3.22} \]

由于\(R_1\)和\(R_3\)有着相同的两端电压，同时根据\((3.3.4)\)

\[\Delta V_{EB}=V_{EB1}-V_{EB2}=\frac{kT}{q}ln(\frac{J_2}{J_1}) \tag{3.3.23} \]

将\((3.3.22)\)代入\((3.3.21)\)有：

\[V_{ref}=V_{EB1}+\frac{R_3}{R_2}\frac{kT}{q}ln(\frac{R_3}{R_1}) \tag{3.3.24} \]

因此有：

\[K=\frac{R_3}{R_2} \tag{3.3.25} \]

例题1：

基于本节图（a）中的结构求出带隙基准源中的电阻，其中\(I_1=80\mu A\)，\(I_2 =8\mu A\)，当温度为\(T=300K\)时，\(V_{EB1-0}=0.65V\)。

解答：

根据\((3.3.12)\)有：

\[V_{ref-0}=1.24V \tag{3.3.26} \]

因此，从\((3.3.18)\)中可以得到：

\[V_{R1}=V_{ref-0}-V_{EB1-0}=0.59V \tag{3.3.27} \]

同时，由于\(V_{R3}=V_{R1}\)，我们有：

\[R_3=\frac{V_{R3}}{I_2}=\frac{0.59V}{8\mu A}=73.8k\Omega \tag{3.3.28} \]

并且：

\[R_1=R_3\frac{I_2}{I_1} = 7.38k\Omega \tag{3.3.29} \]

因此，考虑到\((3.3.13)\)，我们有：

\[K=\frac{(1.24-0.65)V}{0.0258\times ln(10)}=9.93 \tag{3.3.30} \]

因此：

\[R_2=\frac{R_3}{K}=7.43k\Omega \tag{3.3.31} \]

需要注意的是，使用\((3.3.23)\)以及\(J_1/J_2=I_1/I_2\)（因为\(Q_1\)和\(Q_2\)的尺寸相等），我们有：

\[\Delta V_{EB}=\frac{kT_0}{q}ln(\frac{I_1}{I_2})=59mV \tag{3.3.32} \]

计算出的温度相关度为\(0.198mV/K\)，这在上一节的例子1中进行过计算。因此我们需要大概10倍的增益来抵消负温度相关度（在这个例子里精确地说时9.93）。

电压基准源的设计方程同样适用于本节图中（b）的p阱工艺的电路，推导与n阱工艺基本一致。

在CMOS工艺的基准源实现时，大电阻一般通过阱电阻实现。然而不幸的是这些电阻也有着温度相关度，根据[Michejda, 1984]，其大致为：

\[R(T)=R_0\frac{T^{\eta}}{T_0^{\eta}} \tag{3.3.33} \]

其中\(\eta = 2.2\)。这个误差可以通过将\(V_{ref-0}\)略微偏置在比\((3.3.11)\)略高的值来抵消，即：

\[V_{ref-0}=V_{G0}+(m+\eta -1)\frac{kT_0}{q} \tag{3.3.34} \]

假定电阻的温度效应最小化，主要的误差源来自于放大器的输入失调电压[Michejda, 1984]。这会导致\(\Delta V_{BE}\)的方程里多出一个\(K\)倍于输入失调电压的误差项。例如，一个\(1mV\)的失调电压可能会产生一个温度相关度（TC），大致由下式[Song, 1983]给出：

\[TC_{error}\approx 26ppm/^\circ C \tag{3.3.35} \]

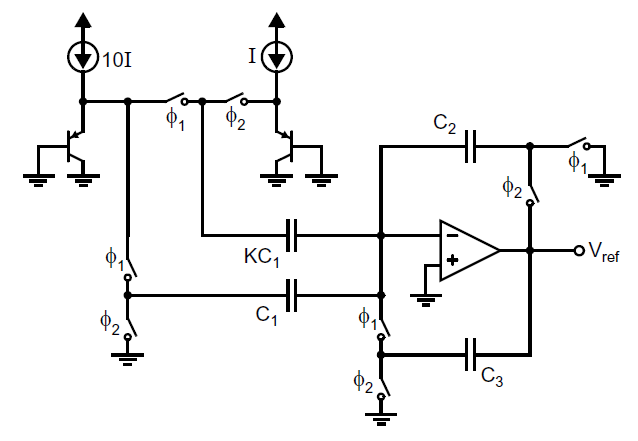
一个减小放大器输入失调引入的误差的方法是使用带有输入失调补偿的开关电容（SC）放大器电路[Song, 1983]。下图展示了一种可能的开关电容电压参考源结构，其实用了[Martin, 1987]提出的放大器。该放大器在电路中能够使得输出时刻有效，并且对于放大器的有限增益问题更加不敏感。后续讨论开关电容电路时我们还会详细介绍。

假定放大器的输入失调已经最小化，带隙电压基准仍然存在固有的温度相关度，如我们在\((3.3.15)\)中所见。此外，更进一步的附加温度相关度来自于\(V_{G0}\)会随着温度产生轻微的变化（上面的分析中忽略了这个因素）。这两个因素总共加在一起，将最好的能够取得的温度相关度控制在了\(25ppm/K\)附近。最小化二阶效应超出了本文的讨论范畴，但是感兴趣的可以参考[Palmer, 1981; Meijer, 1982; Song, 1983]来看这些例子如何尽可能减小二阶效应引入的误差。

一种CMOS带隙基准源的替代实现方案可见[Degrauwe, 1985]，其中使用了横向的npn阱电阻。在[Tzanateas, 1979]中，电压基准源基于通过两个MOS晶体管偏置在弱反型时的栅源电压之差产生的PTAT电压。感兴趣的读者可以看这些文章。

本节虽然对带隙基准进行了一些讨论，但是因为参考的这本书比较老，没有介绍太多参考源方面的先进技术。但上面描述的经典结构仍然是目前教科书中最常介绍的一种，也足够应付一些基础的应用，这篇知乎文章有更多详细的讨论。

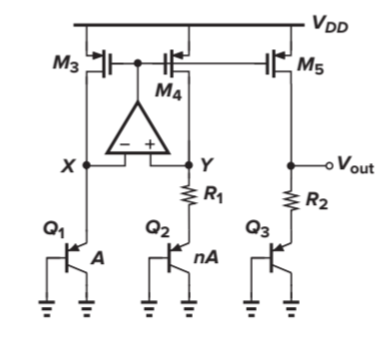
下图中的电路结构与本节之前介绍的略有不同，从原理上来说，仍然是利用放大器虚短特性，\(X\)和\(Y\)点电压相等，同时\(M_{3-5}\)电流镜使得各支路上电流相同，因此：

\[V_X=V_{EB1}=V_Y=V_{EB2}+V_{R1}=V_{EB2}+I_1R_1 \tag{3.3.36} \]

故：

\[\Delta V_{EB}=V_{EB1}-V_{EB2}=\frac{kT}{q}ln(\frac{nA}{A})=\frac{kT}{q}ln(n)=V_{R1}=I_1R_1 \tag{3.3.37} \]

又考虑到：

\[V_{out}=V_{EB3}+V_{R2}=V_{EB3}+I_2R_2 \tag{3.3.38} \]

同时因为电流镜，\(I_2=I_1\)，因此：

\[V_{out}=V_{EB3}+I_1R_2=V_{EB3}+\frac{R_2}{R_1}\frac{kT}{q}ln(n) \tag{3.3.39} \]

所以\(K=R_2/R_1\)，只需要合适调整两个电阻之比就可以抵消正负温度相关度。此外上述的带隙基准电路是存在为零的简并点的，因此和上节介绍的固定偏置电路一样，需要考虑通过引入启动电路来使得基准源能够自己离开零简并点。

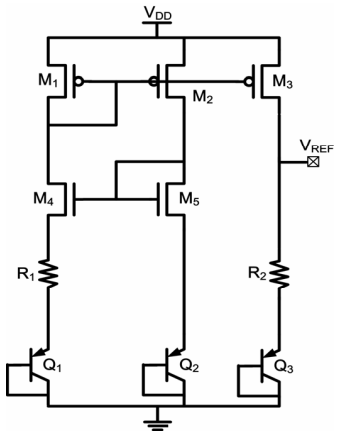
当然，这个电路也可以用一个更简化的电路方案来实现，放大器形成的\(V_X=V_Y\)通过下图中的钳位晶体管\(M_4\)和\(M_5\)来完成，使得\(M_4\)和\(M_5\)的源极电压相同：

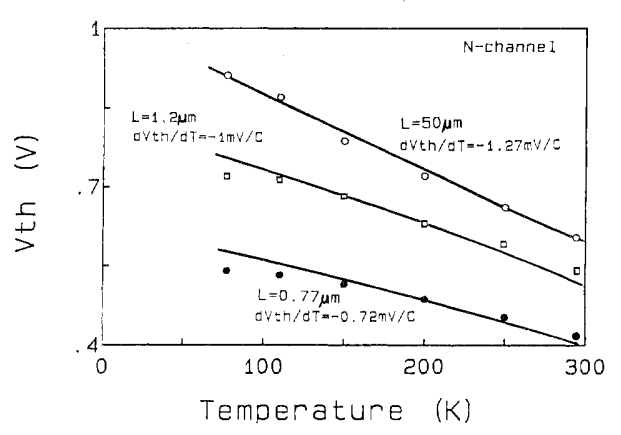
还有一种电压基准结构利用了MOS晶体管阈值电压的负温度相关度来构建，这篇论文对MOS晶体管阈值电压的温度相关度进行了讨论，对于一个n沟道晶体管来说，其阈值电压会随着温度的增大而减小。

从理论上进行推导，n沟道晶体管阈值电压的方程为：

\[V_{tn}=V_{tn-0}+\gamma (\sqrt{2\phi_F+V_{SB}}-\sqrt{2\phi_F}) \tag{3.3.36} \]

其中\(V_{tn0}\)为参考阈值电压，\(\gamma\)为衬底调制因子，\(\phi_F\)为费米势是与温度有关的因子：

\[\phi_F=\frac{kT}{q}ln(\frac{N_A}{n_i}) \tag{3.3.37} \]

首先我们假定\(V_{tn-0}\)与温度无关，那么我们将\(V_{tn}\)对\(T\)求偏导可以得到：

\[\frac{\partial V_{tn}}{\partial T}=\frac{\partial V_{tn}}{\partial \phi_F}\frac{\partial \phi_F}{\partial T}=\gamma (\frac{1}{\sqrt{2\phi_F + V_{SB}}}-\frac{1}{\sqrt{2\phi_F}})\times \frac{k}{q}ln(\frac{N_A}{n_i}) \tag{3.3.38} \]

当\(V_{SB}>0\)时，显然\(\partial V_{tn}/\partial T <0\)。这里我们求出的是衬底偏置效应随着温度变化对阈值电压的影响。

但如果\(V_{SB}=0\)，\(V_{th-0}\)由于也包含了表面势，其同样会呈现出负温度相关度，可以参考这篇文章中的仿真结果。实际上对于NMOS的阈值电压表达式，模集书中一般会给出的公式形如\((3.3.36)\)，与一般半导体器件物理中给出的阈值电压公式形式上的差别比较大。包括上面的论文里也采用是完全不同于\((3.3.36)\)的形式进行了计算，但最后的结果总体来说应该都会是一致的，即n沟道晶体管阈值电压随温度升高而降低，抛开衬底偏置，完全从表面势的角度进行这里可以参考这篇文章里的推导。

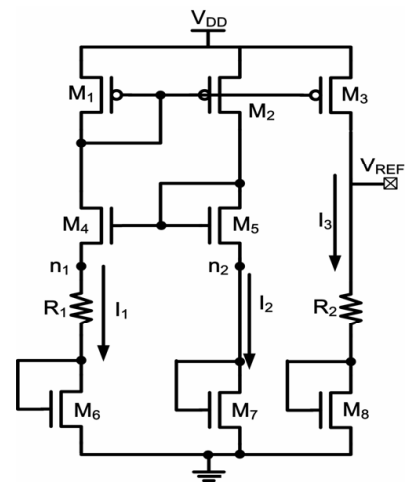
如果我们想利用晶体管阈值电压的负温度特性来构建带隙基准，这里有两篇结构类似的参考论文，论文1，论文2，如下图所示的结构去掉了BJT，其中\(M_4\)和\(M_5\)管子起到类似于运放的作用，通过钳位的方式控制\(V_{n1}=V_{n2}\)，然后与上面的BJT电路分析过程类似，可以得到：

\[V_{ref}=V_{GS8}+\frac{R_2}{R_1}(V_{GS7}-V_{GS6}) \tag{3.3.39} \]

假设偏置电流通过温度无关的电流基准产生的情况下，我们知道根据平方律：

\[I_{D}=\frac{1}{2}\mu_nC_{ox}\frac{W}{L}(V_{GS}-V_{tn})^2 \tag{3.3.40} \]

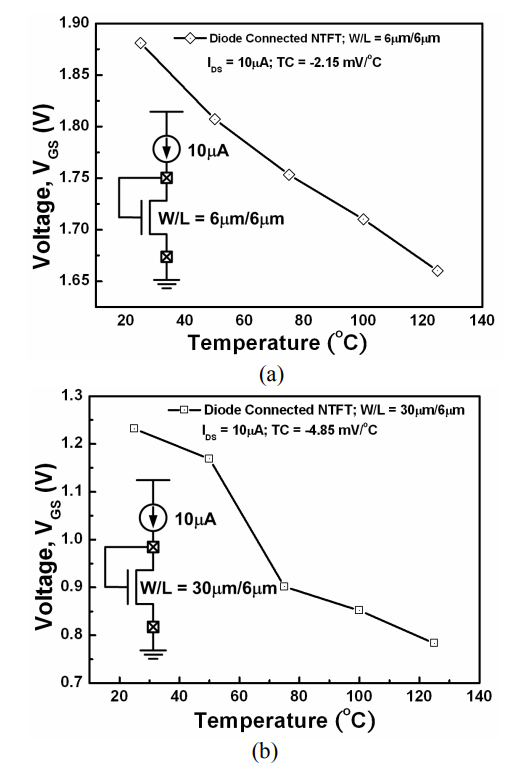
那么，当\(V_{tn}\)跟随温度增大而减小，同时\(I_{D}\)不变的情况下，\(V_{GS}\)也会跟随\(V_{tn}\)一同减小。因此相当于二极管接法的\(M_{6-8}\)的\(V_{GS}\)也获得了\(V_{tn}\)的负温度相关度，参考下图所示，对于二极管接法的NMOS来说，其\(V_{GS}\)相对温度的扫描曲线是随着温度增大而下降的，此外相等\(I_{DS}\)的情况下，长宽比也会对温度相关度产生影响，相同\(L\)的情况下，更大\(W\)的会使得温度相关度的绝对值更大：

接下来的问题就是如何利用\(M_{6-7}\)的栅源电压之差获取正温度相关度。根据\(I_1=I_2\)我们知道：

\[\frac{1}{2}\mu_nC_{ox}(\frac{W}{L})_6(V_{GS6}-V_{tn6})^2=\frac{1}{2}\mu_nC_{ox}(\frac{W}{L})_7(V_{GS7}-V_{tn7})^2 \\ \Rightarrow \sqrt{(\frac{W}{L})_6}(V_{GS6}-V_{th6})=\sqrt{(\frac{W}{L})_7}(V_{GS7}-V_{th7}) \tag{3.3.41} \]

根据上面的讨论我们知道对于两根偏置在相同电流下，但是长宽比不同的晶体管，其\(V_{GS}\)温度相关度也不同，而根据之前的推导，我们也知道\(V_{GS}\)实际上是跟随了\(V_{tn}\)的变化，因此在这里我们有必要设\(M_6\)和\(M_7\)有着不同的阈值电压温度相关度\(\partial V_{tn6}/\partial T\)和\(\partial V_{tn7}/\partial T\)。

从\((3.3.41)\)我们可以得到：

\[V_{GS7}-V_{GS6}=(1-\sqrt{\frac{(W/L)_7}{(W/L)_6}})(V_{GS7}-V_{tn7})+(V_{th7}-V_{tn6}) \tag{3.3.42} \]

由于\(I_D\)恒定，所以：

\[V_{GS7}-V_{tn7}=\sqrt{\frac{2I_D}{\mu_nC_{ox}(W/L)}_7} \tag{3.3.43} \]

代入\((3.3.42)\)后：

\[V_{GS7}-V_{GS6}=(\sqrt{\frac{1}{(W/L)_7}}-\sqrt{\frac{1}{(W/L)_6}})\sqrt{\frac{2I_D}{\mu_nC_{ox}}}+(V_{tn7}-V_{tn6}) \tag{3.3.44} \]

对\(T\)进行微分后：

\[\frac{\partial (V_{GS7}-V_{GS6})}{\partial T}=\frac{\partial V_{tn7}}{\partial T}-\frac{\partial V_{tn6}}{\partial T} \tag{3.3.45} \]

从\((3.3.44)\)中我们知道为了\(V_{GS7}-V_{GS6}\)为正值（由于这个压差也是电阻两端的电压，我们必须确保其为正），我们需要取\((W/L)_6>(W/L)_7\)，即相同\(L\)的情况下，\(W_6>W_7\)。同时我们也知道首先\(\partial V_{tn7}/\partial T\)和\(\partial V_{tn6}/\partial T\)均小于0，由于\(W_6>W_7\)，我们有\(|\partial V_{tn6}/\partial T|>|\partial V_{tn7}/\partial T|\)，从而通过\((3.3.45)\)我们可以知道\(\partial(V_{GS7}-V_{GS6})/\partial T >0\)，这就得到了我们想要的正温度相关度。

因此\((3.3.39)\)就得到了负温度相关度项\(V_{GS8}\)和正温度相关度项\(V_{GS7}-V_{GS6}\)，通过比例系数\(K=R_2/R_1\)来控制两者相互抵消，从而得到零温度相关度的\(V_{ref}\)。

此外也有去掉电阻的完全CMOS方案，可以参考这篇论文。