模拟集成电路设计系列博客——3.2.1 基本恒定跨导电路

3.2.1 基本恒定跨导电路

我们知道晶体管的跨导可能是模拟放大器中最重要的参数，因此必须要保持稳定。其稳定性可以通过[Steininger, 1990]首次采用的电路来实现，该电路将晶体管的跨导匹配到一个电阻的电导上。作为结果，对于一阶效应来说，晶体管的跨导独立于电源电压以及工艺和温度误差。

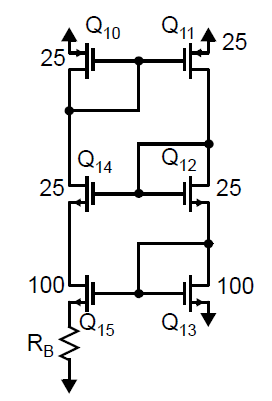
偏置电路如下图所示：

首先假定\((W/L)_{10}=(W/L)_{11}\)。这个等式通过电流镜\(Q_{10}\)，\(Q_{11}\)使得电路的两侧有着相同的电流。作为结果，我们同样有\(I_{D15}=I_{D13}\)，现在围绕\(Q_{13}\)，\(Q_{15}\)和\(R_B\)组成的环路，我们有：

\[V_{GS13}=V_{GS15}+I_{D15}R_B \tag{3.2.1} \]

考虑到\(V_{effi}=V_{GSi}-V_{t}\)，我们可以通过在公式两侧减去阈值电压\(V_t\)，得到：

\[V_{eff13}=V_{eff15}+I_{D15}R_B \tag{3.2.2} \]

这个等式也可以写为：

\[\sqrt{\frac{2I_{D13}}{\mu_nC_{ox}(W/L)_{13}}} = \sqrt{\frac{2I_{D15}}{\mu_nC_{ox}(W/L)_{15}}} + I_{D15}R_B \tag{3.2.3} \]

由于\(I_{D13}=I_{D15}\)，我们可以进一步写成：

\[\sqrt{\frac{2I_{D13}}{\mu_nC_{ox}(W/L)_{13}}} = \sqrt{\frac{2I_{D13}}{\mu_nC_{ox}(W/L)_{15}}} + I_{D13}R_B \tag{3.2.4} \]

重排公式后我们有：

\[\frac{2}{\sqrt{2\mu_nC_{ox}(W/L)_{13}I_{D13}}}[1-\sqrt{\frac{(W/L)_{13}}{(W/L)_{15}}}]=R_B \tag{3.2.5} \]

考虑到\(g_{m13}=\sqrt{2\mu_nC_{ox}(W/L)_{13}I_{D13}}\)，可以的如以下关系式：

\[g_{m13}=\frac{2[1-\sqrt{\frac{(W/L)_{13}}{(W/L)_{15}}}]}{R_B} \tag{3.2.6} \]

\(Q_{13}\)的跨导仅由\(R_B\)和几何参数决定，独立于电源电压，工艺参数和温度，和其他易变的参数。对于\((W/L)_{15}=4(W/L)_{13}\)的特定情况，我们有：

\[g_{m13}=\frac{1}{R_B} \tag{3.2.7} \]

不仅\(g_{m13}\)得到了稳定，其他的跨导也得到了稳定，因为所有的晶体管电路来自于同样的偏置网络，因此电流之比都主要依赖于几何参数之比。例如，对于所有的n沟道晶体管：

\[g_{mi}=\sqrt{\frac{(W/L)_iI_{Di}}{(W/L)_{13}I_{D13}}}\times g_{m13} \tag{3.2.8} \]

对于所有的p沟道晶体管：

\[g_{mi}=\sqrt{\frac{\mu_p}{\mu_n}\frac{(W/L)_iI_{Di}}{(W/L)_{13}I_{D13}}}\times g_{m13} \tag{3.2.9} \]

由于\(g_{m13}\)是个n沟道晶体管，在\((3.2.9)\)出现了额外的项\(\sqrt{\mu_p/\mu_n}\)影响p沟道晶体管的跨导。很不幸的是这个项在芯片之间有着很大的差异，同时也随着温度会有小的变化。

另外上面展示的电路形成了一个正反馈环路，稳定性是一个要重点考虑的问题。晶体管\(Q_{11}\)作为一个共源放大器工作，并放大所有出现在其栅极上的小信号，并以二极管接法的\(Q_{13}\)作为负载。结果信号出现在\(Q_{15}\)的栅极上，而\(Q_{15}\)也作为一个共源放大器工作，\(R_B\)是其源极退化电阻。只要\(R_B\)足够大，第二级的增益就会比单位增益要小，从而保证稳定性。然而，在高频下任意\(R_B\)的寄生参数将会减小其阻抗，并使得电路变得不稳定[Nicolson, 2004]。如果\(R_B\)是一个精确的片外电阻，那么寄生电容因为包含了芯片的Pad和板子会很大。因此有必要至少将一部分的\(R_B\)放在片上。但不幸的是，片上的电阻相对来说很难控制。

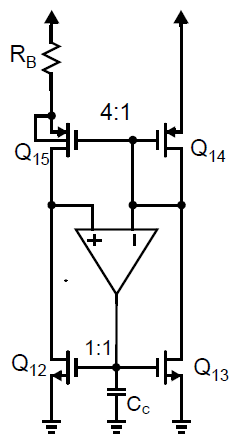
之前的分析忽略了许多二阶效应，例如晶体管输出阻抗和体效应。体效应会略微影响方程，但是关系式仍然主要只取决于几何参数。最主要的限制来源于晶体管的输出阻抗。这两个效应都可以通过下图的电路来消除。晶体管对\(Q_{14}\)和\(Q_{15}\)通过PMOS器件来实现，在多数的CMOS工艺中都可以将\(Q_{15}\)的源极和体端连接到一起来消除体效应。此外，一个放大器被用来保证两个晶体管的漏极电压相等，从而减小有限晶体管输出阻抗的影响。另一个使用放大器的优势是其减小了\(Q_{15}\)的漏极阻抗，从而减小了正反馈环路\(Q_{12-15}\)中的增益并提高了稳定性。包含了放大器和共源晶体管\(Q_{12,13}\)的负反馈环路可以通过合理调节补偿电容\(C_c\)的方式来取得稳定。

不幸的是，上面两种电路都存在一个第二稳定点，即所有的电流都等于零。为了确保这个情况不会发生，有必要增加一个启动电路在所有电路都为零时工作，将电路拖离这个状态。

一个固定跨导偏置的重要限制是在高温度下时，电流和过驱动电压会显著增大来补偿载流子迁移率的减小和保持跨导稳定。受限的信号摆幅会变得显著低于供电电压。由于载流子迁移率正比于\(T^{-3/2}\)，因此温度从室温（\(300K\)）到100℃（\(373K\)）时会产生27%的减少。有效栅源电压需要增大27%来使得晶体管跨到不变，根据公式：

\[g_{mi}=\mu_iC_{ox}(\frac{W}{L})_i V_{eff-i} \tag{3.2.10} \]

只要过驱动电压一开始没有设计的太大，这个限制在多数应用中都是可以容忍的。一个典型的室温下的过驱动电压值为\(0.2V\)到\(0.25V\)。