模拟集成电路设计系列博客——2.1.3 两级放大器的补偿

2.1.3 两级放大器的补偿

这一小节讨论了在闭环中使用放大器，以及如何来补偿放大器使得闭环不仅稳定，而且会有一些其他的良好特性。尽管使用两级放大器作为例子，但是这里讨论的情况大部分也可以用于其他的放大器。

放大器的最优补偿一般被认为是放大器设计过程中中最困难的环节，但是采用这里使用的系统方法，就可以沿着一个直接的过程来获得一个接近最优的补偿网络。

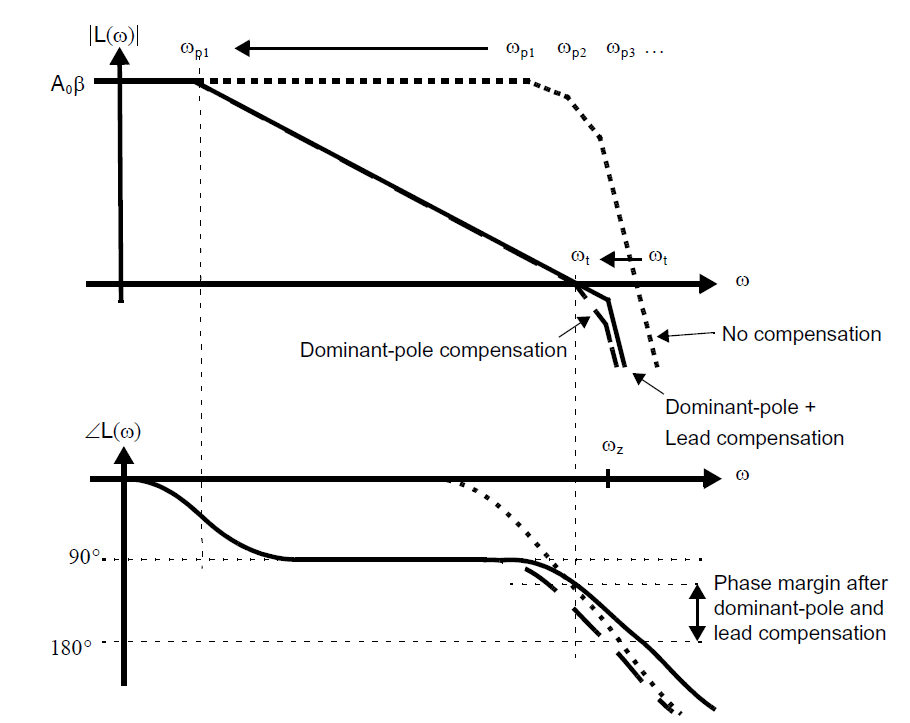
两个对于模拟电路设计者来说最受欢迎的工具分别是主极点补偿和超前补偿。主极点补偿通过强制使得一个反馈系统直到单位增益频率的开环响应近似等于一阶响应来实现。一阶反馈系统只有在至少90°以上相位裕度才能达到无条件稳定。不幸的是放大器电路放大器电路往往产生多个极点和零点。增大电路中极点的频率往往不是很实用，因为这往往需要增大功耗或者是其他的设计取舍。因此，最简单的让系统表现得像一阶系统的方式是有意的降低主极点的频率，使其远低于系统的其他零极点。下图展示了采用这个方案的系统开环响应\(L(\omega)\)，考虑到\(L(\omega)\)是放大器响应和反馈网络响应之积\(A(\omega)\beta\)。在主极点补偿时极点频率\(\omega_{p1}\)被降低到一个低很多的频率。其结果是\(L(\omega)\)的单位增益频率\(\omega_t\)的减少和相位裕度的增加。

进一步增加相位裕度可以通过超前补偿的方式来引入一个比\(\omega_1\)略大的左半平面零点\(\omega_z\)。如果处理得当，这样几乎不会对单位增益频率产生影响，但是能够在单位增益频率处额外增加大概+20°的相移。从而可以在特定的相位裕度下能够比只使用主极点补偿取得更高的单位增益频率。

如下图所示，主极点补偿和超前补偿对低频环路增益和其他的零极点几乎没有影响。根据具体的待补偿结构，情况可能会变得更加复杂，接下来将以经典的两级放大器结构为例子来仔细说明。

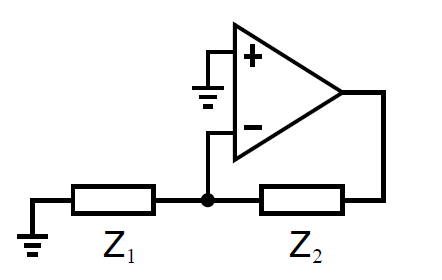
稳定性与信号裕度取决于反馈放大器\(L(s)\)的环路增益，尽管之前我们的分析都只集中在放大器的频率响应\(A_v(s)\)上，但是在计算补偿时，反馈网络是必须要被考虑的。如下图展示了一个无驱动网络，并假定放大器有着极高的输入阻抗和远小于负载或反馈网络的输出阻抗，则其环路增益可以被近似为：

\[L(s)\approx A_{v}(s)\frac{Z_1}{Z_1+Z_2} \tag{2.1.31} \]

这里令\(\beta = Z_1/(Z_1+Z_2)\)并假定直到环路的单位正义频率\(\beta\)都保持为定值。（注意在精确确定相位裕度时，仍然需要通过仿真来确定负载的影响，这里只是做了近似的处理）。电容\(C_c\)控制主极点\(\omega_{p1}\)，以及环路单位增益频率\(\omega_t\)：

\[\omega_t=L_0\omega_{p1}=\beta g_{m1}/C_c \tag{2.1.32} \]

因此通过合理选择\(C_c\)的值就能够控制主极点补偿。

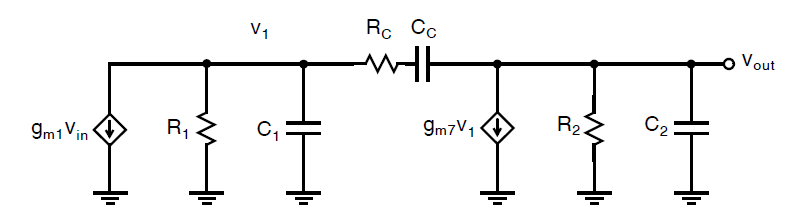
超前补偿通过电阻\(R_c\)来实现。假设之前做过的这一小信号模型中\(R_c\)不为零（在上一节分析时我们将其设为了0），重新分析之后会发现前两个极点的位置仍然几乎保持不变，第三个极点处于一个非常高的频率几乎不产生影响。然而零点的表达式会变化为：

\[\omega_z=\frac{-1}{C_c(1/g_{m7}-R_c)} \tag{2.1.33} \]

这使得设计者有了多种选择，比如可以取：

\[R_c=1/g_{m7} \tag{2.1.34} \]

来完全消除右半平面零点。也可以将\(R_c\)取得更大从而将右半平面零点移动到左半平面来抵消非主极点。令\((2.1.33)\)和\((2.1.27)\)相等则可以得到：

\[R_c=\frac{1}{g_{m7}}(1+\frac{C_1+C_2}{C_c}) \tag{2.1.35} \]

第三种方案，也是比较推荐的方案是将\(R_c\)取得更大，将左半平面零点移动到一个比没有\(R_c\)时的单位增益频率略大频率点上[Roberge, 1975]。例如，如果现在新的零点频率取在比单位增益频率大70%的位置，那么其会引入一个\(tan^{-1}(1/1.7)=30°\)的相位超前，在这种情况下应该满足公式：

\[\omega_z=1.7\omega_t \tag{2.1.36} \]

假定\(R_c >> (1/g_{m7})\)，那么\(\omega_z=1/(R_cC_c)\)，根据\((2.1.32)\)，\(\omega_t=\beta g_{m1}/C_c\)，可以选取出\(R_c\)为：

\[R_c \approx \frac{1}{1.7\beta g_{m1}} \tag{2.1.37} \]

最后，超前补偿电阻\(R_c\)一般可以用一个工作在线性区的晶体管来替换，如下图所示。由于没有直流偏置电流流通，晶体管\(Q_9\)的\(V_{DS9}=0\)，因此\(Q_9\)处于深线性区，晶体管以电阻\(R_c\)的状态工作，其值为：

\[R_c=r_{ds9}=\frac{1}{\mu_cC_{ox}(W/L)_9 V_{eff9}} \tag{2.1.38} \]

需要被注意的是这里的\(r_{ds}\)表示的是\(Q_9\)在线性区的源漏电阻，需要和\(Q_9\)在饱和区时的输出阻抗做一个区分。无论晶体管工作在饱和区还是线性区，\(r_{ds}\)都用来表示源漏电阻，一个简单的确定\(r_{ds}\)使用的公式的方法是确定晶体管处于哪个工作区里。

总结一下补偿一个两级放大器的具体过程：

1. 首先选定\(C_c^{'}\approx (\beta g_{m1}/g_{m7})C_L\)，这使得环路的单位增益频率\((2.1.32)\)大致处在一个第二极点的位置\((2.1.27)\)，假定第二极点位置由电容\(C_L\)主导。

2. 仿真找到-125°相移的频率，设这点的增益为\(A^{'}\)，这点的频率为\(\omega_t\)，因为我们希望将这个频率设置为环路的单位增益频率。

3. 选择一个新的\(C_c\)使得\(\omega_t\)成为环路的单位增益频率，从而带来55°的相位裕度（因为我们在第二步中选择了-125°），这可以通过设置\(C_c\)为：

   \[C_c=C_c^{'}A^{'} \tag{2.1.39} \]

   来实现。

4. 选择\(R_c\)为：

   \[R_c=\frac{1}{1.7\omega_tC_c} \tag{2.1.40} \]

   这样选择能够进一步增加大约30°的相位裕度，从而带来总体85°的相位裕度。给工艺误差留出了5°的裕度。这个选择几乎是所有使用电阻串联补偿电容的放大器进行超前补偿时的最优选项。后续还得数次调整\(R_c\)来优化相位裕度，因为\((2.1.40)\)假定了\(R_c>>1/g_{m7}\)，而且单位增益频率可能会由于超前补偿而发生漂移。但是设计者需要检查增益在新的单位增益频率之后继续稳步下降，否则电路可能会因为在略大于\(\omega_t\)处引入了意外的零点，导致电路的瞬态响应变差。

5. 在第4步做完后如果信号裕度还是不够，那么可以在保持\(R_c\)不变的情况下增大\(C_c\)，从而将\(\omega_t\)和超前零点搬移到更低的频率，同时保证他们的比例大致固定，因此最小化其他不会移动到更低频率的高频零极点的影响。在大多数情况下，高频零极点（除了超前零点）在\(C_c\)增加时都不会显著地移动到更低的频率上。

6. 最后一部是将\(R_c\)换成晶体管，晶体管的尺寸可以通过\((2.1.38)\)来确定。最后再次仿真修改器件尺寸，按照步骤4和5来调优信号裕度。

上述步骤不仅可以用于两级放大器，几乎同样的步骤也可以用于实现许多其他放大器的最优补偿。

例题：

放大器开环传递函数如下：

\[A(s)=\frac{A_0(1+s/\omega_z)}{(1+s/\omega_{p1})(1+s/\omega_{p2})} \tag{2.1.41} \]

这里\(A_0\)是放大器的直流增益，\(\omega_z\)，\(\omega_{p1}\)和\(\omega_{p2}\)分别是零点、主极点、次极点的频率。假定\(\omega_{p2}=2\pi \times 50MHz\)，\(A_0=10^4\)，放大器设置在单位增益环路中，即\(\beta =1\)，\(L(s)=A(s)\)。

1. 假定\(\omega_z \rightarrow \infty\)，求\(\omega_{p1}\)和单位增益频率\(\omega_t^{'}\)，使得放大器的单位增益裕度有55°
2. 假定\(\omega_z = 1.7\omega_t^{'}\)，其中\(\omega_t^{'}\)为第一问中求出的结果，求出新的单位增益频率\(\omega_t\)，以及新的相位裕度

解答：

首先注意到在频率远高于主极点时\((\omega>>\omega_{p1})\)，例如单位增益频率。\((2.1.41)\)可以简化为：

\[L(s)=A(s)=\frac{A_0(1+s/\omega_z)}{(s/\omega_{p1})(1+s/\omega_{p2})} \tag{2.1.42} \]

使用\(\omega_z \rightarrow \infty\)代入\((2.1.42)\)，我们可以求出\(\omega_t^{'}\)：

\[\angle A(j\omega_{t}^{'})=-90°-tan^{-1}(\omega_t^{'}/\omega_{p2}) \tag{2.1.43} \]

对于所需的相位裕度\(PM=55°\)，我们需要：

\[\angle A(j\omega_t^{'})=-180°+PM=-125°\tag{2.1.44} \]

利用\((2.1.43)\)和\((2.1.44)\)，我们可以求出：

\[tan^{-1}(\omega_t^{'}/\omega_{p2})=35° \Rightarrow \omega_t^{'}=2.2\times 10^8 rad/s = 2\pi \times 35MHz \tag{2.1.45} \]

.令\(|A(j\omega_t^{'})|=1\)，再次使用\((2.1.42)\)，有：

\[\frac{A_0}{(\omega_{t}^{'}/\omega_{p1})\sqrt{1+(\omega_{t}^{'}/\omega_{p2})^2}}=1 \Rightarrow \omega_{p1}=\frac{\omega_t^{'}\sqrt{1+(\omega_{t}^{'}/\omega_{p2})^2}}{A_0}=2\pi \times 4.28KHz \tag{2.1.46} \]

这样第一问就解决了。

接着，我们现在设:

\[\omega_z=1.7\omega_t^{'}=2\pi \times 59.5MHz \tag{2.1.47} \]

为了求出新的单位增益频率，将\((2.1.42)\)中设\(|A(j\omega_t)|=1\)：

\[\frac{A_0\sqrt{1+(\omega_t/\omega_z)^2}}{(\omega_{t}/\omega_{p1})\sqrt{1+(\omega_{t}/\omega_{p2})^2}}=1 \Rightarrow \omega_t=\frac{A_0\omega_{p1}\sqrt{1+(\omega_{t}/\omega_{z})^2}}{\sqrt{1+(\omega_{t}/\omega_{p2})^2}} \tag{2.1.48} \]

使用该方程可以求解出新的单位增益频率。可以使用\((2.1.46)\)中求出的\(\omega_t^{'}\)作为初始值，迭代求解\((2.1.49)\)，在四次迭代后，可以求出\(\omega_t =2\pi \times 39.8MHz\)，单位增益频率比原始的\(\omega_t^{'}\)增大了14个百分点，可以求出新的相移为：

\[\angle A(j\omega_t)=-90°+tan^{-1}(\omega_t/\omega_z)-tan^{-1}(\omega_t/\omega_{p2})=-85° \tag{2.1.49} \]

在之前的基础上又提升了30°的相位裕度，达到了85°。但在实践中由于额外的高频零极点的存在（这里做了忽视），实际的相位裕度提升不会有这么大，但无论这种降低有多少，超前补偿带来的相位裕度提升都是巨大的。

接下来我们将讨论如何实现对工艺和温度不敏感的超前补偿，根据公式\((2.1.15)\)和公式\((2.1.27)\)，我们有：

\[\omega_t = \frac{g_{m1}}{C_c} \tag{2.1.50} \]

和

\[\omega_{p2} \approx \frac{g_{m7}}{C_1+C_2} \tag{2.1.51} \]

我们发现第二极点频率和第二级的驱动管跨导\(g_{m7}\)成正比，同时单位增益频率与输入级的输入管跨导\(g_{m1}\)成正比。这些跨导的比例一般是随着工艺和温度变化也能保持很顶的，因为这些跨导被同样的偏置网络决定。同时，此外，大多数电容也相互跟踪，因为它们主要由栅氧化层决定。根据\((2.1.33)\)，当电阻被用于实现超前补偿时，超前零点的频率由下式给出：

\[\omega_z=\frac{-1}{C_c(1/g_{m7}-R_c)} \tag{2.1.52} \]

因此，如果\(R_c\)能够跟踪跨导的变化，尤其是\(1/g_{m7}\)，那么超前零点也能随着\(Q_7\)的跨导成比例的变化。从而超强零点可以与\(\omega_t\)和\(\omega_{p2}\)以及其他高频零极点保持固定的相对频率。换而言之，超前补偿是最独立于工艺和温度变化的。

如果\(R_c\)是通过一个栅源电压和\(Q_7\)的成正比的线性区晶体管来实现的，那么其\(R_c\)就可以和\(1/g_{m7}\)成正比，因为考虑到\(R_c\)是通过\(Q_9\)来实现的，我们有：

\[R_c=r_{ds9}=\frac{1}{\mu_nC_{ox}(W/L)_9V_{eff9}} \tag{2.1.53} \]

同时\(g_{m7}\)为：

\[g_{m7}=\mu_cC_{ox}(W/L)_7V_{eff7} \tag{2.1.54} \]

因此\(R_cg_{m7}\)之积将为一个常数：

\[R_cg_{m7}=\frac{(W/L)_7V_{eff7}}{(W/L)_9V_{eff9}} \tag{2.1.55} \]

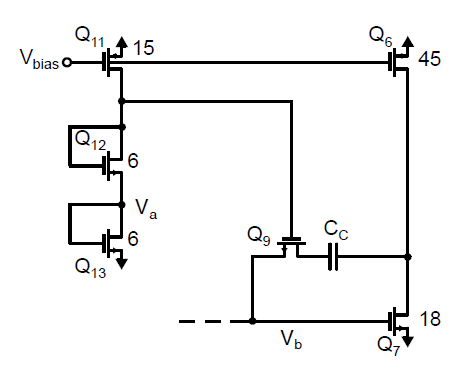
因此只需要确保\(V_{eff9}/V_{eff7}\)为一个独立于工艺和温度变化的定值就行（剩下的项都是几何尺寸，很容易固定比例）。\(V_{eff9}/V_{eff7}\)可以通过使得相同的驱动电流来驱动\(V_{GS9}\)和\(V_{GS7}\)来保持一个定值。考虑如下图所示的电路，其由一个偏置级，一个第二级还有两级放大器的补偿网络构成。

首先我们取\(V_a=V_b\)，从而使得\(V_{eff13}=V_{eff7}\)。这两个过驱动电压可以通过下式来确保相等：

\[\sqrt{\frac{2I_{D7}}{\mu_nC_{ox}(W/L)_7}}=\sqrt{\frac{2I_{D13}}{\mu_nC_{ox}(W/L)_{13}}} \tag{2.1.56} \]

对上式做化简后：

\[\frac{I_{D7}}{I_{D13}}=\frac{(W/L)_7}{(W/L)_{13}} \tag{2.1.57} \]

而\(I_{D7}/I_{D13}\)是通过电流镜\(Q_6\)，\(Q_{11}\)来设置的，因此：

\[\frac{I_{D7}}{I_{D13}}=\frac{(W/L)_6}{(W/L)_{11}} \tag{2.1.58} \]

因此结合\((2.1.57)\)和\((2.1.58)\)，我们得出只需要满足下面的关系式就能够使得\(V_{eff13}=V_{eff7}\)：

\[\frac{(W/L)_7}{(W/L)_{13}}=\frac{(W/L)_6}{(W/L)_{11}} \tag{2.1.59} \]

如果上述条件满足，我们有\(V_{eff13}=V_{eff7}\)，因此我们有\(V_a=V_b\)。由于\(Q_{12}\)和\(Q_9\)的栅极短接，并且他们的源极电压相同，所以我们有\(V_{eff12}=V_{eff9}\)，下一步，使用栅源电压的关系和\(I_{D12}=I_{D13}\)，我们能够有：

\[\frac{V_{eff7}}{V_{eff9}}=\frac{V_{eff13}}{V_{eff12}}=\frac{\sqrt{2I_{D13}/\mu_nC_{ox}(W/L)_{13}}}{\sqrt{2I_{D12}/\mu_nC_{ox}(W/L)_{12}}}=\sqrt{\frac{(W/L)_{12}}{(W/L)_{13}}} \tag{2.1.60} \]

将\((2.1.60)\)代入到\((2.1.55)\)后，我们发现\(R_cg_{m7}\)由下式给出：

\[R_cg_{m7}=\frac{(W/L)_7}{(W/L)_9}\sqrt{\frac{(W/L)_{12}}{(W/L)_{13}}} \tag{2.1.61} \]

即只与几何尺寸有关，而与工艺温度变化无关。

因此我们可以使得线性区晶体管的源漏电阻与另一个晶体管的跨导能够成反比例关系。这个关系在其他很多的应用中也很有用。例如可以让所有晶体管的跨导和一个片外电阻的跨导匹配，从而使得片上通过线性区晶体管实现的电阻和一个片外的电阻保持一个固定的比例。这个关系在现代电路设计中非常有用。