Loading

基于存算一体技术的新型计算机体系结构

1. 经典计算机体系结构

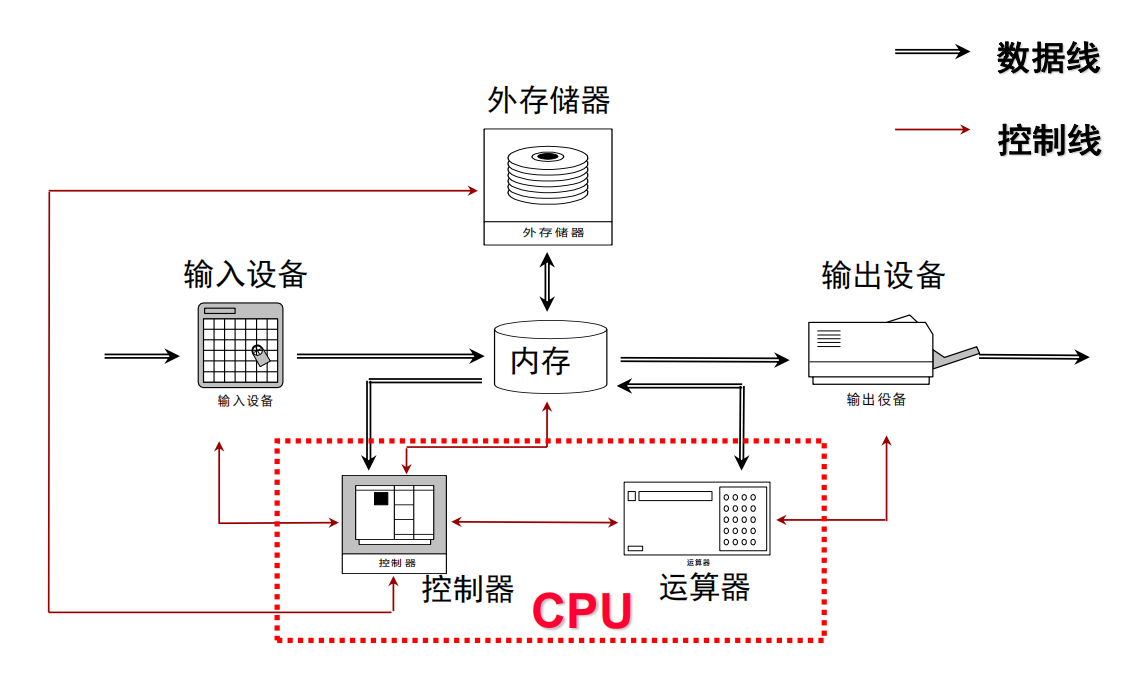
经典计算机体系结构的基本思想由冯.诺伊曼提出，因此也被成为冯.诺伊曼架构。其主要的主要的思想是计算机由计算器，存储器，控制器，输入设备和输出设备五个部分组成。

这一思想指导了经典计算机体系结构的发展，并奠定了现代计算机的基本结构，以一台普通的家用台式机为例：运算器&控制器：CPU、GPU，存储器：内存、硬盘，输入设备：鼠标、键盘，输出设备：屏幕、音响......但这并不代表体系结构技术自其提出以来就不再进步，事实上为了应对不断增长的应用需求，体系结构技术也有大量的内部革新（当然，背后最大的动力来自于摩尔定律带来的半导体工艺进步）。

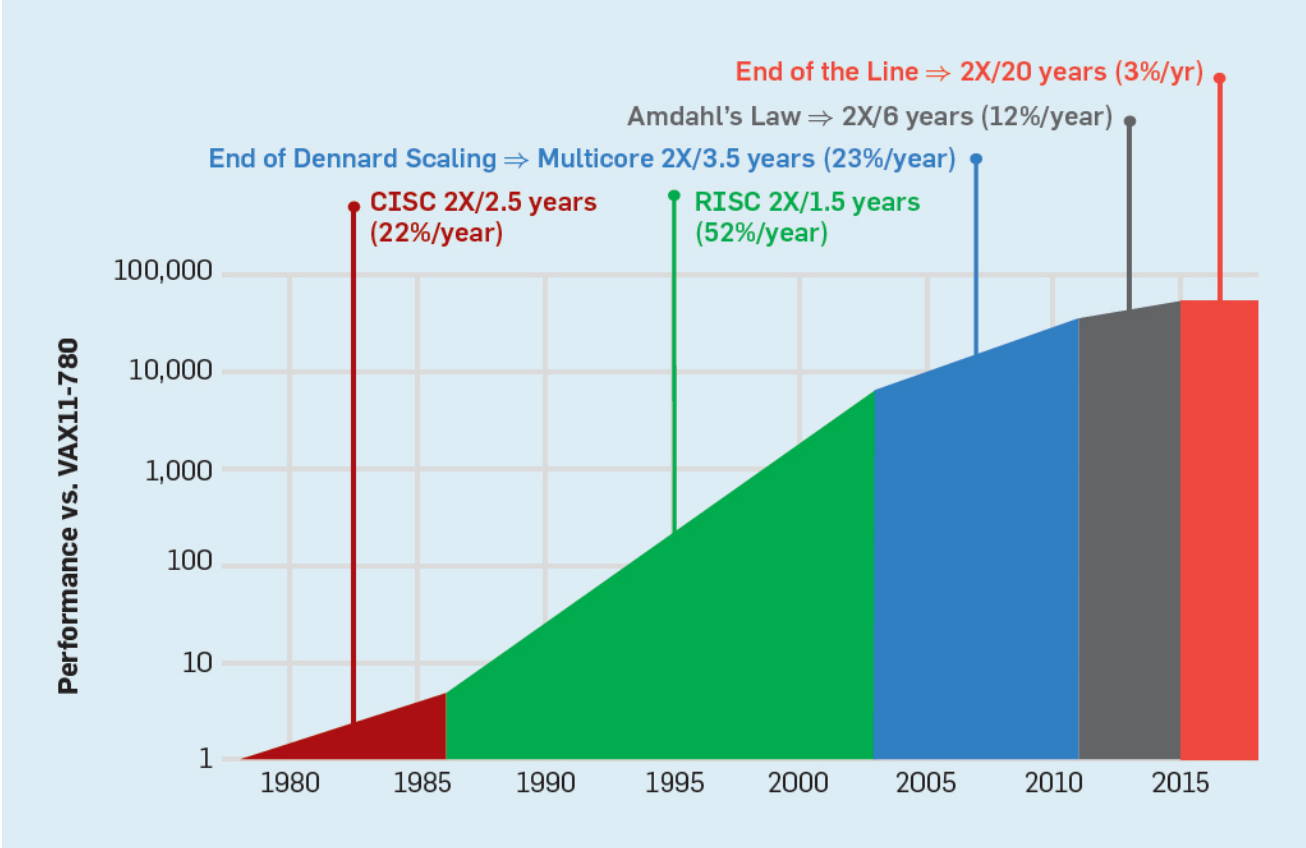
这些革新主要围绕冯式体系中运算器，控制器和存储器的部分。对于运算器&控制器来说，可以分为CPU和GPU两条线，CPU的技术革新的主线在流水线，指令集方面的不断优化，体现在主频的不断提高[1]。当单核的性能提升出现困难以后CPU走向多核时代，这种趋势延续至今，目前的主流CPU在通过Chiplet技术进一步提升核数从而提高性能。

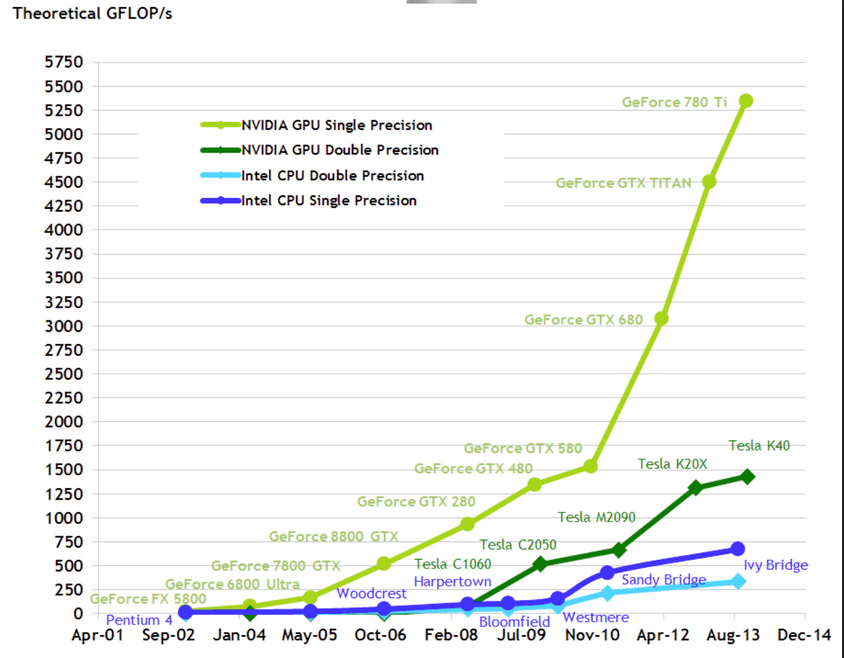
而GPU则是从CPU中逐渐分离出来成为独立的计算机部件，一开始的GPU主打向量计算，主要执行计算密集的图形类任务从而降低CPU上的计算负载。GPU具有高计算并行度的特点，因此算力提升远远快于CPU。在AI时代到来以后GPU由于对高算力需求的AI应用的极佳支持而迅速成为宠儿。

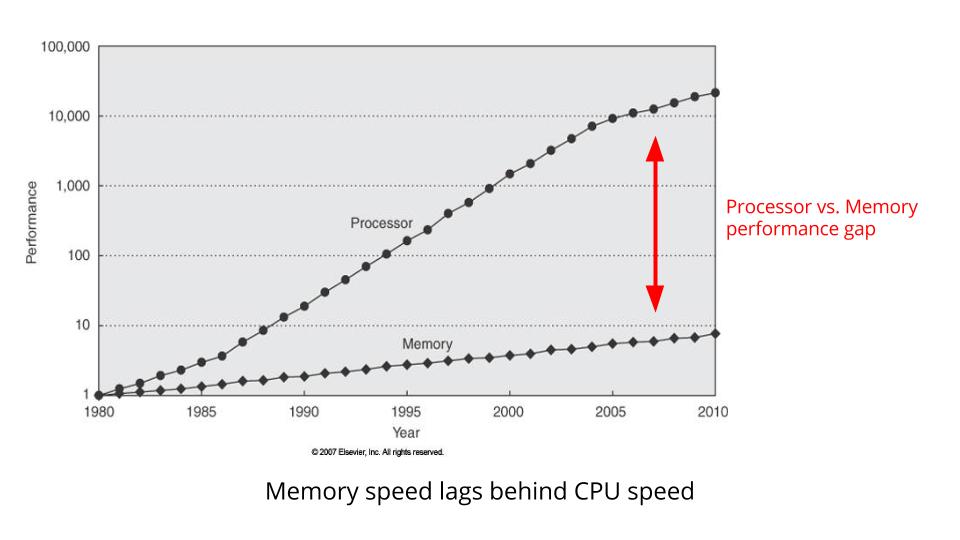
对于存储器来说，由于冯式结构存储与计算分离的特点，随着计算端性能的逐步提升，对于访存端的需求持续提高，但两者的性能增长速度却是前者远快于后者，形成了剪刀差，这就是“存储墙”问题，亦称作冯.诺伊曼瓶颈[2]。

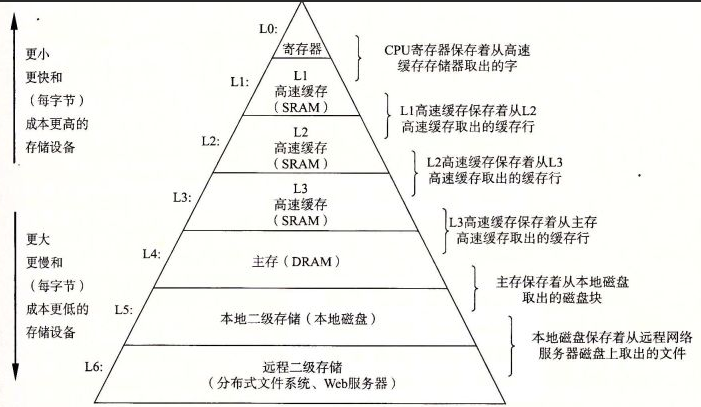
经典体系结构对于这一问题的解决方案包括：将指令访存与数据访存分离（即所谓的哈佛结构），以及划分多级存储层次——利用程序的时间局部性和空间局部性，将经常要被访问的数据放在靠近计算器&控制器的高速存储介质里，而对于不经常被访问的数据则放在远离计算器&控制器的慢速存储介质里，时至今日这仍然是经典体系结构中对于存储墙问题的解决方案，在过去的几十年间的变化主要是缓存层次的不断增加，缓存容量不断扩大，以及提出更好地利用局部性提高访存性能的一些优化手段。

2. AI时代的计算机体系结构

随着摩尔定律走向终结，经典体系结构的增长也逐步趋缓，然而随着深度学习技术的加速发展，算法的算力需求开始暴增。本人撰写的大模型溯源讨论了神经网络规模与神经网络性能的增长关系，可以预见，在不久的未来，随着大模型时代的到来，算法将对硬件提出指数级别的算力增长需求。这一趋势的到来将极大的冲击经典体系结构——其中的一个表现就是GPU在体系结构里的后来居上，在社会层面上体现为GPU大厂NVIDIA在2020年完成了对CPU大厂Intel的市值反超，尽管也有其他的业务因素，但AI带来的强劲增长动力在其中也起到了相当决定性的作用。

GPU虽然独领风骚，但挑战者仍层出不穷，这里的原因在于GPU虽然在算力方面表现强悍，但仍然存在缺陷——1. 其不擅长处理控制流复杂的程序 2. 其在数据密集型任务的性能上也往往并非最优。而这两个缺陷所造成的结果是，前者带来了异构计算范式，后者则带来了各类专用处理器。

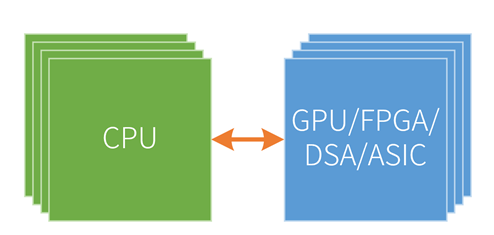
异构计算范式的思路是：任何一类架构都不得不在通用性与专用性之间作出trade-off，追求通用性的代价必然是在专用任务上性能无法达到最优，但一味追求专用任务上的性能提升则容易造成能够解决的问题范围极度狭窄，因此直接将具有通用性和专用性的不同类型的架构统筹成一个系统，根据实际的应用情况，在编写程序时将任务分配到最合适的硬件上，从而实现通用性和专用性之间的平衡。异构计算的思想驱动下，诞生了诸如CPU+GPU，CPU+FPGA，CPU+DSA，CPU+ASIC等多种方案，但其根本思想都是一致的[3]。

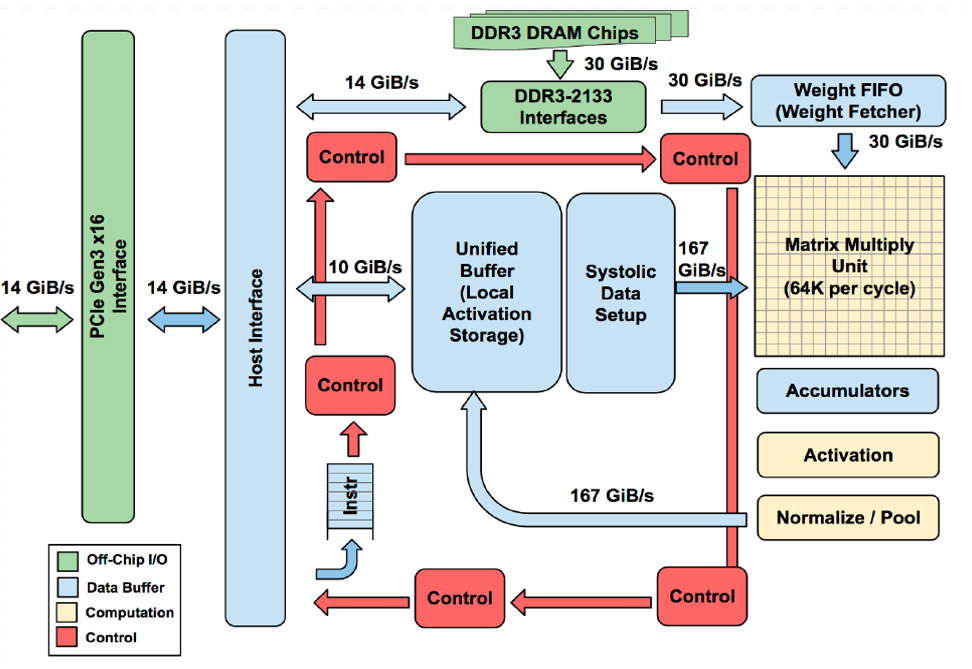
而各类专用处理器的思维则是：针对任务负载的特性，充分在硬件设计上做好适配，以实现最优化。包括但不限于数字信号处理器(DSP)、图像处理器(GPU)、深度学习处理器(AI 芯片)和网络处理器(NPU)等，其主要的特点是针对算法的本身的结构进行了定制化，一般简化了控制流，但对数据流进行了高度的优化（包括访存，计算等），例如流水线优化，高并行度计算等，因此往往在专用任务上有极佳的表现[4]。一个典型的专用处理器产品是谷歌的神经网络处理器TPU，可以看到其硬件成分与神经网络架构的高度对应。

因此需要反思的问题是“AI时代，我们需要什么样的体系结构”。这里必须要认清的是，AI时代的计算特点包括：1. 更加复杂多样的任务类型 2. 极速增长的AI算力需求。针对前者，意味着单一类型的芯片难以满足各类业务场景，异构计算必然是大势所趋，针对后者，AI专用处理器仍然大有可为，如何做到在大型神经网络的推理训练任务上表现出超越当前范式的极佳性能是最主要的问题。

因此在设计新型体系结构时必须扣住这两个关键点：1. 如何融入异构计算框架中，与其他计算芯片（尤其是CPU）共存，这包括数据分享，编程模型等一系列细节技术问题。2. 如何适应大模型计算的需求，这里既包括对主流编程架构的支持（Pytorch，Tensorflow，MXNet），也包括提高协同能力以适应多卡的分布式训练。

3. 存算一体技术

上一节论述完了AI时代的体系结构，但需要注意到的问题是，上述的所有计算形式，包括异构计算，专用处理器等，都仍然没有脱离冯式计算机的范畴，进而，随着算力需求的增长，冯式瓶颈这一计算机体系结构的幽灵愈发恼人。尽管通过暴力增大Cache，暴力提升DRAM带宽等方式能够满足一时的算力增长需求，但这绝非长久之计。

存算一体技术早在1990 年代以来(最初的想法可以追溯到1970 年代)，就收到了研究人员的关注， 当时的关键思想是通过将计算单元放置在内存 (DRAM) 中，将计算单元和内存单元物理耦合在一起，这种思想被成为PIM（Process In Memory）。由于逻辑器件的工艺与存储器件的工艺在集成上的不兼容，当时这一方案并获得成功。然而，自 2010 年代以来，商用 3D 堆叠存储器的出现重新激发了人们对这一方案的兴趣，例如,美光的 Hybrid Memory Cube (HMC) 在堆叠的 DRAM 层下合并了一个逻辑层，可以在逻辑层内实现自定义逻辑。

PIM 现在经常被称为近存计算，以避免与存内计算混淆，存内计算是一种新的以内存为中心的计算范式，它继承了PIM和近存计算的精神。近存计算实现了独立
于内存结构的逻辑电路，而存内计算则密切涉及内存单元、内存阵列和计算中的外围电路。通常需要对它们进行结构修改或增加额外的特殊电路来支持计算。
从历史上看，存内计算曾被认为是一种经济上不可行的设计。修改内存单元给内存设计增加了不小的成本，存内计算的技术需要深度优化当前内存架构的存储单元结构。 此外，修改后的单元将大大降低密度，这可能会使以存内计算架构难以证明其性能与面积（或性能与成本）的权衡是合理的。
随着非易失性存储器 （NVM）的出现,存内计算的概念被重新审视。 某些 NVM 具有理想的物理特性，可以在模拟域中执行计算，从而在对内存阵列的设计更改最少的情况下实现存内计算。 此外，存储单元的非易失性解决了 DRAM 存内计算的破坏性读取访问问题，即执行计算前必须执行一次复制。 但另一方面，模拟域中的存内计算仍然是一种有待优化的技术。 例如，各种非理想因素，如存储器件的差异性，电路内部噪声和传输线损耗等可能会影响计算结果。 此外，随着模拟信号的转换处理的位数增加，数模转换 （DAC） 和模数转换 （ADC）成本将变得过高。
随着这一趋势，研究人员重新审视了为基于当前各类存储介质（即 SRAM、DRAM 和 NAND Flash还有各种新型存储器）设计的存内计算，并主要致力于解决上述挑战以及利用了这些存储器的成熟技术[5]。

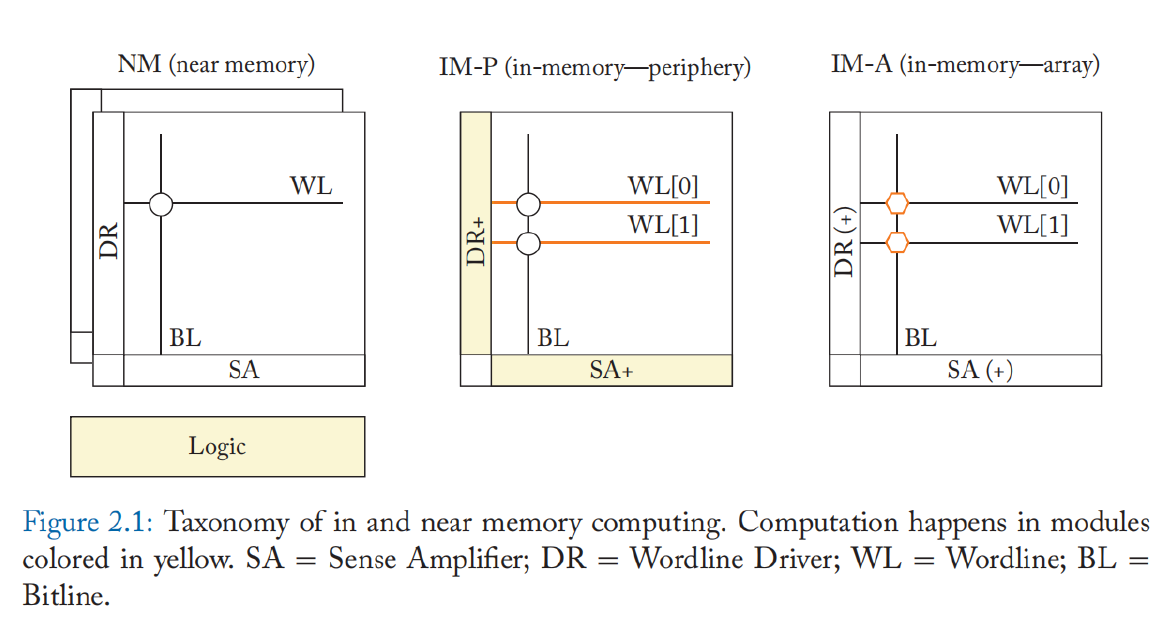
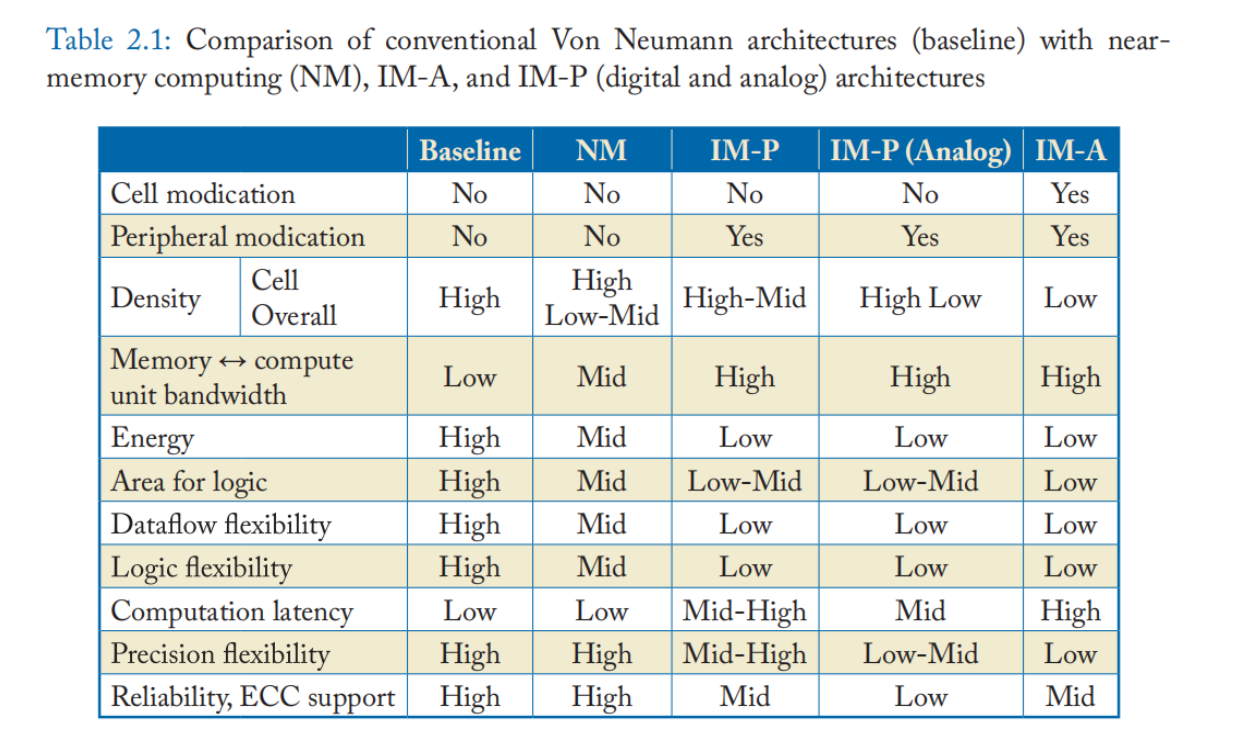
上图给出了近存计算和存内计算的两种模式，近存计算不对存储阵列作出任何修改，主要是将逻辑单元摆放在接近存储阵列的位置上。而存内计算则分为在外围电路产生计算结果的IM-P（In-Memory-Periphery）方式和在阵列内部产生计算结果的IM-A（In-Memory-Array）方式。

IM-P 可以进一步分为仅处理数字信号的数字IM-P 方法和在模拟域中执行计算的模拟 IM-P 方法。 修改后的外围电路能够实现超出正常读/写的操作,例如与不同的单元交互或加权读电压。 此类修改包括支持字线驱动器中的多行激活以及用于多级激活和感测的 DAC/ADC。 它们被设计用于实现从逻辑运算到算术运算的多种运算类型，例如向量矩阵乘法中的点积。 虽然结果是在外围电路中产生的,但存储器阵列执行了大量的计算。对外围电路的改变可能需要与传统存储器中使用的阵列不同的电流/电压读写方式。 因此，IM-P 可能会修改存储单元来提高鲁棒性。 此外，用于支持复杂功能的外围设备的附加电路可能会导致高成本。

IM-A 架构可以提供最大的带宽和能源效率，因为计算完全发生在存储阵列内部。 IM-A 可以为简单的操作提供最大的吞吐量，但其复杂的操作可能会导致高延迟。 此外，IM-A 经常需要为这种特殊的计算操作重新设计存储单元，修改正常的位线和字线结构。 由于单元和阵列的设计和布局针对特定电压/电流读写进行了高度优化。因此单元和阵列的访问方法的变化需要进行大量的重新设计工作。 此外，有时需要修改外围电路（即执行读写操作所需的逻辑电路，例如字线驱动器和读出放大器）以支持 IM-A 计算。

上表对传统冯诺依曼架构（Baseline）、近存计算 (NM)、IM-A 和 IM-P 架构进行了单元、外围电路修改程度，密度，内存到计算单元之间的带宽，能耗，逻辑单元面积，数据流灵活性，计算延迟，精度灵活性和可靠性（ECC支持性）等多个角度的比较。整体上来看，越靠近冯式结构，灵活性与可靠性越好，而越靠近IM-A架构，带宽和能耗表现越好。

4. 基于存算一体技术的新型计算机体系结构

本节我们将讨论基于存算一体技术的新型计算机体系结构的核心思想。首先我们需要明确设计目标：

  1. 符合AI时代计算机体系结构的发展趋势
  2. 解决存储墙问题。

因此综合下来有如下几个设计原则：

  1. 要具备异构计算的兼容性，这代表所设计的结构要有对外的数据通路与指令通路。
  2. 面向AI大模型的计算优化，这包括对网络模型的适应性，对多卡&分布式训练的支持。
  3. 在访存方面能够实打实的解决冯式瓶颈问题，这要求不仅要应用存算技术，而且要能够在足够大的AI应用上，展现出对GPU等芯片的性能优越性。

从芯片类型的角度上来说，基于存算的AI芯片介于DSA和ASIC之间，需要具有可编程性以应对不同网络结构的数据流，但也不需要为了过多的编程性牺牲性能，在设计指令集时要考虑这一点。在此我们要针对性分析AI算法的特点，并考虑如何与存算范式进行结合。

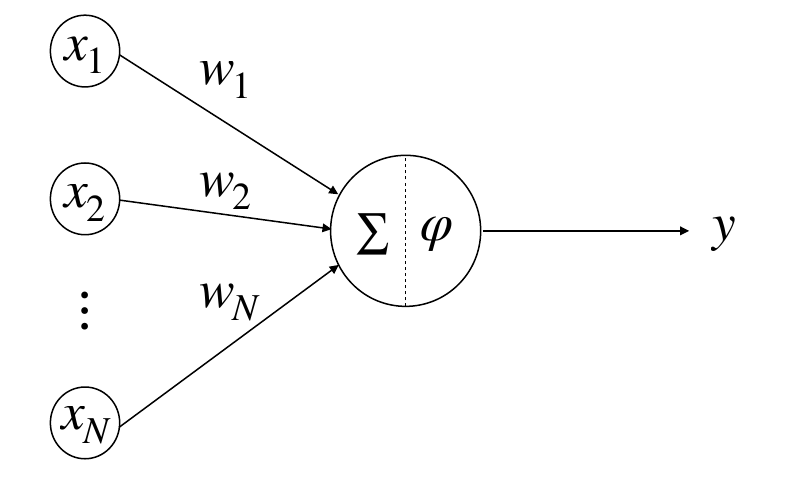
目前AI运算的实质是多个人工神经元的大量堆叠：

从公式上表达为：

\[y=\phi(\sum_{i=1}^Nx_i\times w_n) \]

从算法的角度出发，这个公式的元素分别是y：输出，\(\phi\)：激活函数，x：输入，w：权重值。由于一层神经元的输出也是下一层神经元的输入，因此两者可以统称为激活值（activation）。

从体系角度的结构出发，这个公式里面则可以分为计算，访存，控制。计算的部分主要是激活值与权重值的向量乘（对于多个神经元构成的一层神经网络来说则是矩阵向量乘），称为朴素矩阵乘（General Matrix Multiplication，GEMM）（这部分的计算量往往能占到90%以上），以及激活函数构成的非线性运算。

访存的部分主要是激活值和权重，这两者存在不同的特性，激活值是随着输入更新而不断更新的，因此存在频繁读写的需求，而权重是固定的，除非因为片上存储有限而无法存储全部权重，否则原则上权重不应该产生读写。

控制的部分最主要的是数据流——激活值的更新与流动，权重值的更新，其次非线性运算的执行。

针对每一部分进行更详细的分析，我们可以确定以下几个设计原则：

  1. 计算矩阵乘：算力优化的关键，存算技术的应用核心，直接影响处理器指标。
  2. 计算非线性：算力优化的难点，计算种类多，功能复杂，需要在吞吐上与计算矩阵乘对齐。
  3. 激活值访存：读写频率高，要求高访存灵活性。
  4. 权重值访存：读写频率低，访存灵活性要求低。
  5. 控制流设计：Load/Store指令必须充分考虑网络特性，很大程度影响性能。非线性运算的指令要综合考虑实现性能和成本。

综合上述所有设计原则，我们可以推导出如下架构：

Weight Storage要求使用大容量存储介质，读写不频繁，而且具有存算能力，那么NVM就是最佳介质。我们在NVM上部署大规模存算，就能实现极佳的算力集成。Activation Storage由于需要频繁读写，而且容量要求上相对没有那么大，DRAM是很合适的存储介质（在出现能够替代DRAM的存储介质之前）。剩下的逻辑部分要分成两块，一块是放置在同时靠近Weight Storage和Activation Storage两边的逻辑单元，这部分单元主要通过近存计算技术计算神经网络中的非线性部分，同时也执行访存控制功能。另一块放置在Activation Storage外围，执行input embedding。

这一结构的潜力来源是存储器技术的持续改进和工艺封装技术的进步，Weight Storage所用的NVM的3D堆叠技术使得存储密度快速提升，现在只需要卡片大小的面积就可以实现数TB容量的存储器，Activation Storage目前所使用的DRAM在工艺微缩和3D堆叠上遇到的困难更大一些，但新的2T0C技术提出也有可能突破这一技术瓶颈。先进封装技术则可以将上述存储介质和逻辑单元实现晶圆级三维集成封装，最后我们会获得一个可能只有移动硬盘大小的超级电脑（可以基于现在的迷你电脑产品，比如Intel的NUC，或者苹果的Macmini展开想象，但体积更小，算力更强），其散热问题主要是关注先进散热技术的发展，以及通过NVM存算技术的超高能效尽可能减少能耗。

这里可能会有的问题是：

  1. 基于3D NVM的存算技术发展还不成熟。
  2. DRAM工艺发展瓶颈。
  3. 先进封装技术实现多晶圆堆叠还不成熟。
  4. 芯片级散热技术发展不够快。
  5. 迷你超算之间如何高效互联构成更大算力网络的机理。
  6. 新型架构的编程模式会是什么。

5. 参考资料

  1. 《计算机体系结构（第二版）》胡伟武、汪文祥等 ↩︎

  2. 《性能之殇（一）-- 天才冯·诺依曼与冯·诺依曼瓶颈》https://lvwenhan.com/tech-epic/492.html ↩︎

  3. 《异构计算面临的挑战和未来发展趋势》https://mp.weixin.qq.com/s/urI63skk7Yfn92S993I-6Q ↩︎

  4. 《专用处理器比较分析》鄢贵海 卢文岩 李晓维 孙凝晖 ↩︎

  5. 《In-/Near-Memory Computing》Daichi Fujiki, Xiaowei Wang etc. ↩︎

posted @ 2023-02-20 10:33  sasasatori  阅读(1318)  评论(0)  编辑  收藏  举报