各类存算方式性能分析

说明

主要针对模拟/数字方式的存内计算，与近存计算方式进行性能分析，以便于在后续开展工作前进行性能估计以指导计算架构的选择。一般衡量算力会使用TOPS/W或者TOPS/mm2作为标准，但这两者实际上是时延，功耗和面积三者衍生的量。如TOPS/W可以用功耗和延迟来计算，TOPS/mm2可以用面积和延迟来计算，因此在对架构进行分析时采用时延，功耗和面积三个更基础的物理量，在实际设计时可以根据自身的需求去进行三个设计量之间的trade-off。

架构

模拟存内计算架构：

数字存内计算架构：

近存计算架构：

对比

N为输入比特位数，模拟存算，数字存算与近存计算模式均默认采用串行编码输入。

\(T_{Array}\)代表单次访问存储单元的时间，\(P_{Array}\)代表访问单次访问存储单元的功耗。

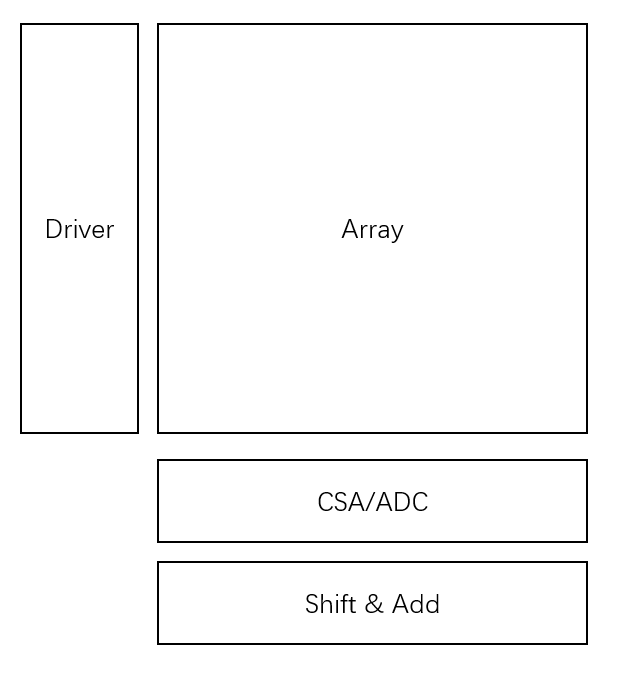
模拟存内计算（CSA读出）

时延：\(T_{total}=T_{Driver}+N*T_{Array}+N*T_{CSA}+T_{Shift\&Add}\)

功耗：\(P_{total}=P_{Driver}+N*P_{Array}+N*P_{CSA}+P_{Shift\&Add}\)

面积：\(S_{total}=S_{Driver}+S_{Array}+S_{CSA}+S_{Shift\&Add}\)

特点：对面积消耗较少

精度相对高

Shift&Add电路开销相对大

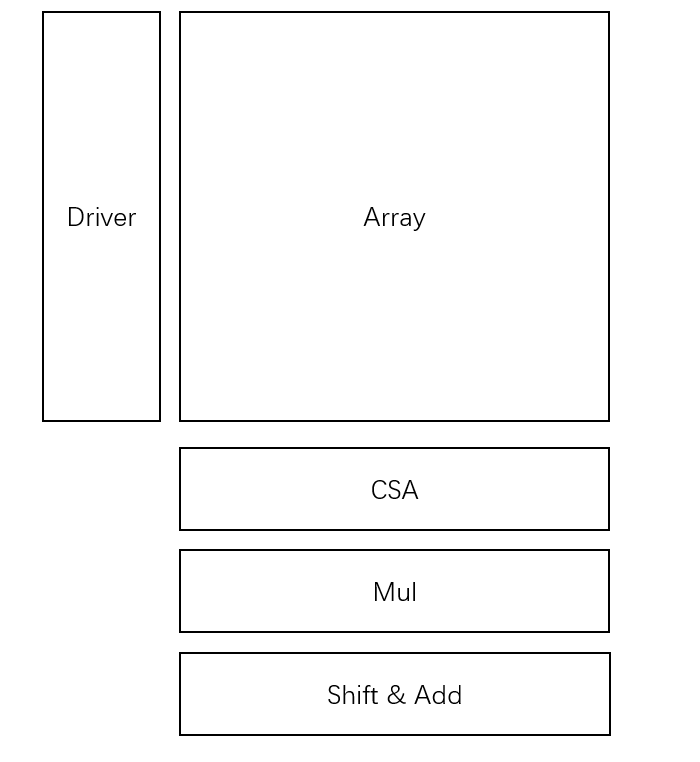
模拟存内计算（ADC读出）

时延：\(T_{total}=T_{Driver}+T_{Array}+T_{ADC}+T_{Shift\&Add}\)

功耗：\(P_{total}=P_{Driver}+N*P_{Array}+P_{ADC}+P_{Shift\&Add}\)

面积：\(S_{total}=S_{Driver}+S_{Array}+S_{ADC}+S_{Shift\&Add}\)

特点：该架构进行存算时需要同时打开多行存储单元，因此在计算功耗功耗时仍然需要乘以比特位数

ADC构成主要的性能瓶颈

相对而言存在更大的精度损失（源于电流汇聚的加法，包括Variation，IR Drop等影响）

高并行度会形成极大的汇聚电流，也对ADC的位数要求越高，当并行度降到最低时（每次只开启一行）则退化成CSA读出

Shift&Add电路开销相对小

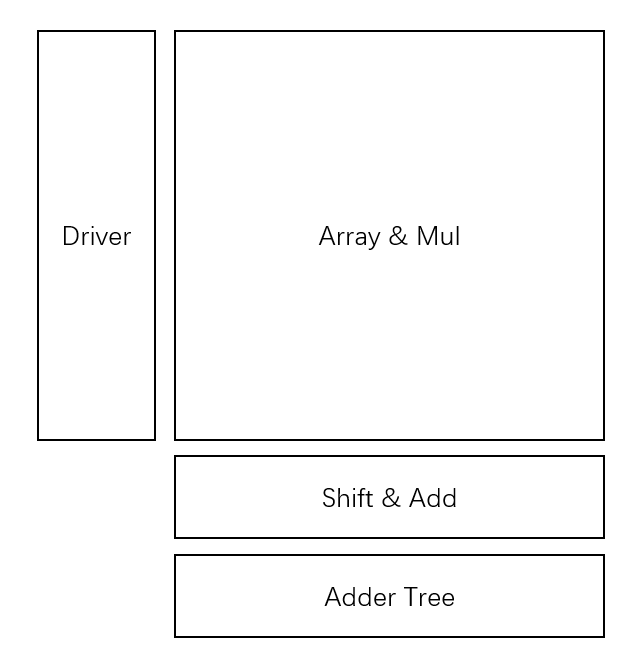
数字存内计算

时延：\(T_{total}=T_{Driver}+T_{Array}+N*T_{Mul}+T_{Shift\&Add}+T_{AdderTree}\)

功耗：\(P_{total}=P_{Driver}+P_{Array}+N*P_{Mul}+P_{Shift\&Add}+P_{AdderTree}\)

面积：\(S_{total}=S_{Driver}+S_{Array}+S_{Mul}+S_{Shift\&Add}+S_{AdderTree}\)

特点：精度高

用逻辑门形成单比特乘法，导致存储密度降低，存储单元需要负担逻辑门的额外面积

催着阵列容量增大逻辑门造成的开销也迅速增大

容量增大后加法器树构成性能瓶颈

近存计算

时延：\(T_{total}=T_{Driver}+T_{Array}+T_{CSA}+N*T_{Mul}+T_{Shift\&Add}\)

功耗：\(P_{total}=P_{Driver}+P_{Array}+P_{CSA}+N*P_{Mul}+P_{Shift\&Add}\)

面积：\(S_{total}=S_{Driver}+S_{Array}+S_{CSA}+S_{Mul}+S_{Shift\&Add}\)

特点：精度高

外部的多比特乘法器开销较大

Shift&Add电路开销相对大