中国科学院大学模数转换器作业开源
1.编写12-bit SAR-ADC的行为级模型:
clear;
%% 信号产生
fclk=1e6; %采样时钟
N=8192; %采样点数
fsig=fclk/N*13; %信号频率
amp=1.0; %信号幅度
vi=amp*sin(2*pi*fsig/fclk*(1:N)); %输入信号
%% DAC电容
w1=[1024,512,256,128,64,32,16,8,4,2,1,0.5];
w2=[1024,512,256,128,64,32,16,8,4,2,1,0.5];
%% sar逻辑
for p=1:length(vi)
vres=vi(p);
dp = 0;
for q = 1:12
if(vres>0)
d=1;
vres=vres-w1(q)/sum(w1);
else
d=0;
vres=vres+w1(q)/sum(w1);
end
dp = dp + d*w2(q);
end
dout(p)=dp;
end
%% 去掉直流量
dout = dout -mean(dout);
%% 画PSD
ed_psd(dout',fsig,fclk,1,'r',0)
其中sar逻辑部分:
最外层循环即对整个信号进行采样,内层循环进行12次比较(对应12bit)
d为比较器输出,vres为残差电压,dp为数字输出(由于DAC最小单位为0.5,所以如果想要获得12bit,即-2048到+2048的整数值需要乘以2),sar逻辑即根据残差电压大于或小于0确定比较器输出,控制DAC更新残差电压,再次进行比较
运行结果:
vin:
dout(量化到12bit后):
1.1计算SNR
function snrdB=ed_psd(x,fin,fs,osr,color,debug)
N=length(x);
data=x;
Ts=1/fs;
N=N-mod(N,2);
f=fin/fs;
FL=1; %in Hertz of lower frequency
FH=fs/2/osr; %in Hertz of higher frequency
fBL=FL/fs*N; %in Bins of lower frequency
fBH=FH/fs*N; %in Bins of higher frequency
data=data';
w=hann_pv(N); %Window function
%w=blackmanharris(N)';
%w=nuttallwin(N)';
%w=kaiser(N,30)';
%w=hodiewindow(N)';
%w=ones(1,N);
[snrdB,ptotdB,psigdB,pnoisedB] = calcSNR(data,f,fBL,fBH,w,N);
ENOBloc=(snrdB-1.76)/6.02
%%%% plot the power spctrum
semilogx(linspace(0,fs/2,N/2), ptotdB(1:N/2), color);
%hold on
%semilogx(linspace(0,fs/2,N/2), pnoisedB(1:N/2), color);
text_handle = text(floor(fs/40),-25, sprintf('SNDR = %4.1f dB \nENOB = %2.2f bits ',snrdB,ENOBloc), ...
'EdgeColor','red','LineWidth',3,'BackgroundColor',[1 1 1],'Margin',10);
grid on;
title('Power Spectral Density','Fontweight','bold','Fontsize',13)
xlabel('Frequency [Hz]','Fontweight','bold')
ylabel('PSD [dB]','Fontweight','bold')
set(gcf,'NumberTitle','off');
set(gcf,'Name', 'Power Spectral Density');
if (debug==1)
figure
noise=pnoisedB(1:N/2);
noise_out=10*log10(sum(10.^(noise/10)))
semilogx(noise,'b*')
end
运行结果:
PSD:
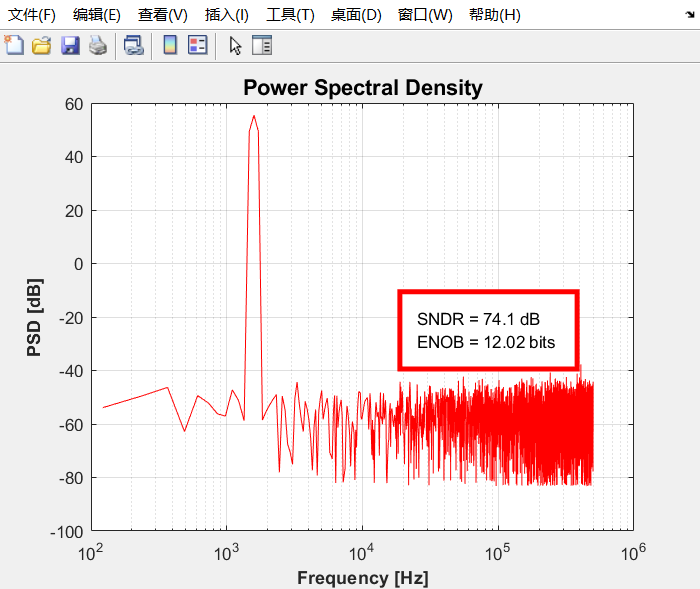
可见SNR达到74.1dB,有效位数达到12bit
1.2研究比较器噪声的影响
为了研究比较器噪声的影响,在sar逻辑部分增加一个高斯白噪声,均值为0,方差可调
%% sar逻辑
for p=1:length(vi)
vres=vi(p);
dp = 0;
for q = 1:12
%% 噪声生成
n = randn * sqrt(0.1);
if(vres + n>0)
d=1;
vres=vres-w1(q)/sum(w1);
else
d=0;
vres=vres+w1(q)/sum(w1);
end
dp = dp + d*w2(q);
end
dout(p)=dp;
end
扫描后,高斯白噪声方差与SNR之间的关系如下表:
| 噪声方差(\(\sigma^2\)) | SNR(dB) |
|---|---|
| 0.1 | 10.9 |
| 0.01 | 20.8 |
| 0.001 | 30.6 |
| 0.0001 | 40.3 |
大致关系为噪声方差减小10倍,SNR提升10dB
不同方差下的信号采样结果:
噪声方差0.1:
噪声方差0.01:
噪声方差0.001:
噪声方差0.0001:
1.3研究DAC电容Mismatch的影响
DAC电容的容值本应该满足\(2^{11}:2^{10}:2^{9}:\dots:2^0\)的比例关系,Mismatch会破坏这一比例关系,导致SNR降低
使用如下DAC权重:
w1=[943,507,274,148,80,43,23,13,7,4,2,1,0.5];
w2=[943,507,274,148,80,43,23,13,7,4,2,1,0.5];
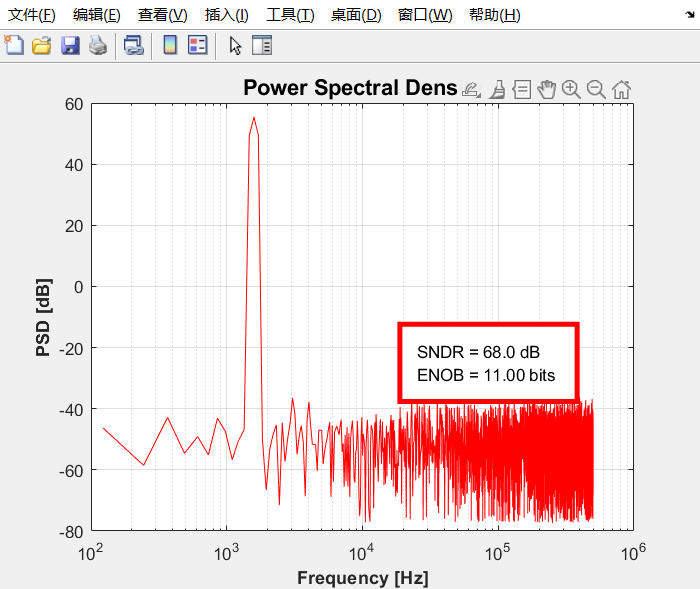
测得SNR下降到68dB,有效位数降低到11bit
2.编写单环3阶1-bit DSM的行为级模型:
clear;
%% 信号产生
fclk=1e6; %采样时钟
N=8192; %采样点数
fsig=fclk/N*13; %信号频率
amp=0.4; %信号幅度
vi=amp*sin(2*pi*fsig/fclk*(1:N)); %输入信号
%% 调制器参数
d=1;x1=0;x2=0;x3=0;vfb=0;
a1=0.3;a2=0.4;a3=0.5;
%% 3阶delta sigma调制器
for p=1:N
x3 = x3 + a3*(x2-vfb);
x2 = x2 + a2*(x1-vfb);
x1 = x1 + a1*(vi(p)-vfb);
test(p)=x1;
if(x3>0)
vfb = 1;
else
vfb =-1;
end
dout(p)=vfb;
end
ed_psd(dout',fsig,fclk,128,'g',0)
3阶DSM的行为级模型如上,其中3阶delta sigma调制器的部分,x1、x2、x3分别为一、二、三级积分器输出。x3送入到1bit量化器,输出+1和-1的判别结果vfb,并反馈到各级积分器中。
运行结果:
vin:
dout(1bit码流):
2.1计算SNR
同样通过ed_psd进行SNR的计算
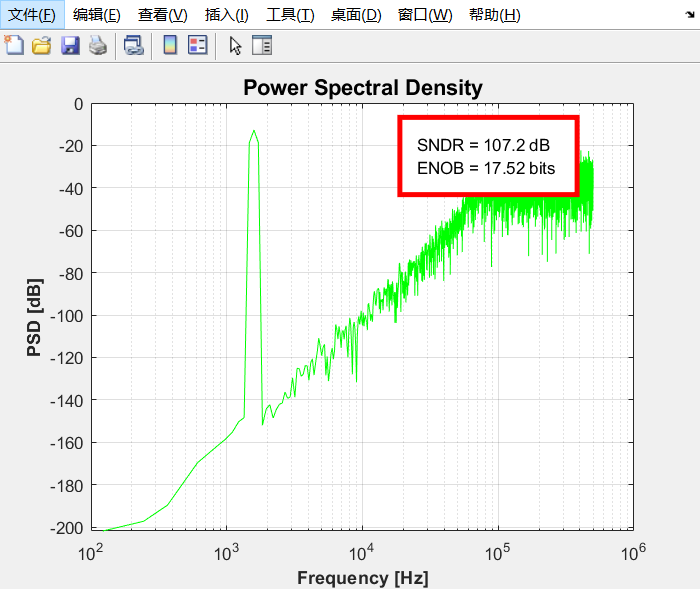
可见SNR达到107.2dB,ENOB达到17bits
2.2研究积分器极点误差的影响
理想放大器中A为无穷大,因此理想积分器系统方程会表示如:
因此对应的差分方程为:
而实际放大器A有限,因此实际积分器系统方程会表示如:
因此对应的差分方程为:
其中\(\alpha\)趋于1,但总小于1,因此会导致极点误差。
这里假设第一级积分器存在极点误差:
%% 3阶sigma delta调制器
for p=1:N
x3 = x3 + a3*(x2-vfb);
x2 = x2 + a2*(x1+vn*randn()-vfb);
x1 =(A-1)/A*x1 + a1*(vi(p)+vn*randn() - vfb);
test(p)=x1;
if(x3>0)
vfb = 1;
else
vfb =-1;
end
dout(p)=vfb;
end
A的取值越小,极点误差越严重
| 放大器增益A | SNR(dB) |
|---|---|
| \(\infin\) | 107.2 |
| 1000 | 104.5 |
| 100 | 102.5 |
| 10 | 92.1 |
可以看到极点误差会造成SNR的下降
3.编写10-bit 时间交织ADC的行为级模型:
clear;
%% 信号产生
fclk=1e6; %采样时钟
N=8192; %采样点数
fsig=fclk/N*13; %信号频率
amp=0.5; %信号幅度
vi=amp*sin(2*pi*fsig/fclk*(1:N)); %输入信号
viq=round(vi*2^10);
%% 定义增益与失调
vos1=0;
vos2=0;
vos3=0;
vos4=0;
g1=1;
g2=1;
g3=1;
g4=1;
%% 4bit时间交织
for p =1:length(viq)
if (mod(p,4)==0)
viq(p) = round((g1*vi(p)+vos1)*2^10);
end
if (mod(p,4)==1)
viq(p) = round((g2*vi(p)+vos2)*2^10);
end
if (mod(p,4)==2)
viq(p) = round((g3*vi(p)+vos3)*2^10);
end
if (mod(p,4)==3)
viq(p) = round((g4*vi(p)+vos4)*2^10);
end
end
ed_psd(viq',fsig,fclk,1,'r',0)
定义了四路SUB-ADC,vi为输入信号,
运行结果:
vin:
viq:
3.1计算SNR
同样通过ed_psd进行SNR的计算
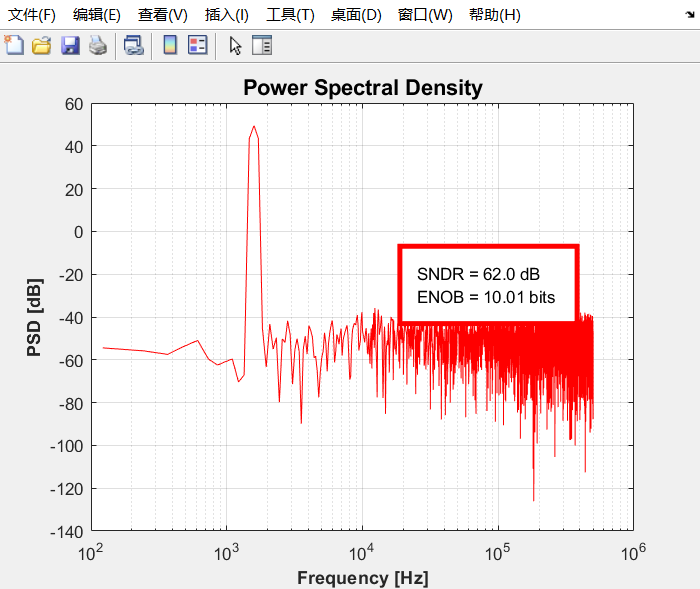
可见SNR达到62dB,ENOB达到10bits
3.2研究失调失配、增益失配的影响
模拟失调失配和增益失配,修改参数如下:
vos1=0.01;
vos2=0.02;
vos3=-0.03;
vos4=-0.04;
g1=1;
g2=1.01;
g3=0.99;
g4=1;
运行结果:
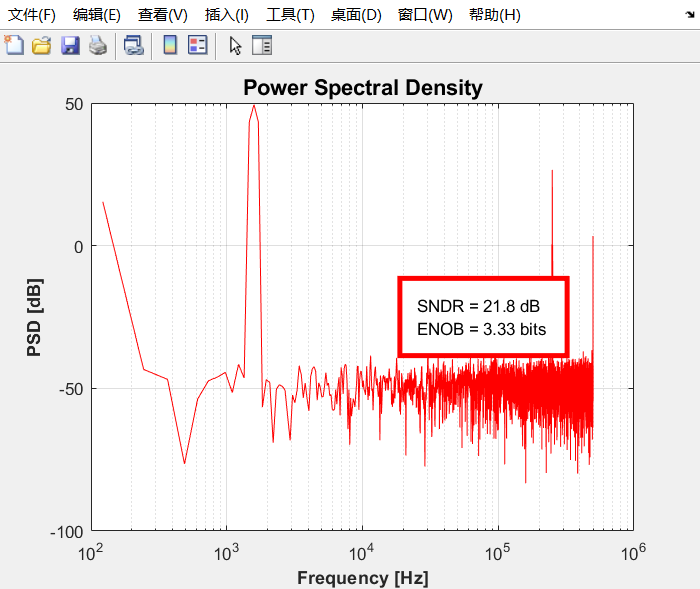
SNR下降到了21.8dB,有效位数下降到3bits
4.编写带有前馈结构的3阶4-bit Delta-Sigma调制器的行为级模型:
clear;
%% 信号产生
fclk=1e6; %采样时钟
N=8192; %采样点数
fsig=fclk/N*13; %信号频率
amp=0.7; %信号幅度
vi=amp*sin(2*pi*fsig/fclk*(1:N)); %输入信号
%% 带前馈的3阶4bit delta sigma调制器
N_bit=4;
Q_level = [-1+2/2^(N_bit):2/2^(N_bit):1-2/2^(N_bit)];
Q_dc = (2^N_bit-1)/2;
d=1;x1=0;x2=0;x3=0;vfb=0;
A = 10000;
a1=0.3;a2=0.6;a3=0.15;
for p=1:N
x3 = x3 + 3*vi(p) - vfb * 3 + x2 + 3*x1;
x2 = x2 + x1;
x1 = x1 + (vi(p) - vfb);
d = sum(x3>Q_level);
vfb = (d-Q_dc)/Q_dc;
dout(p) = (d-Q_dc)/Q_dc;
end
ed_psd(dout',fsig,fclk,128,'g',0)
3阶4bit前馈DSM的行为级模型如上,其中3阶delta sigma调制器的部分,x1、x2、x3分别为一、二、三级积分器输出。x3送入到4bit量化器,判别结果vfb,并反馈到各级积分器中。这里的量化器使用了flash结构,直接与16个Q_level进行比较输出结果。
运行结果:
vin:
dout(4bit码流):
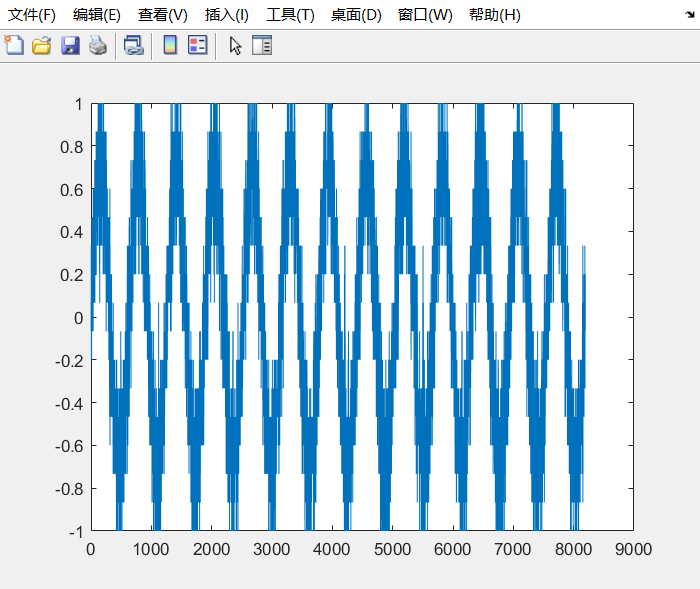
psd:
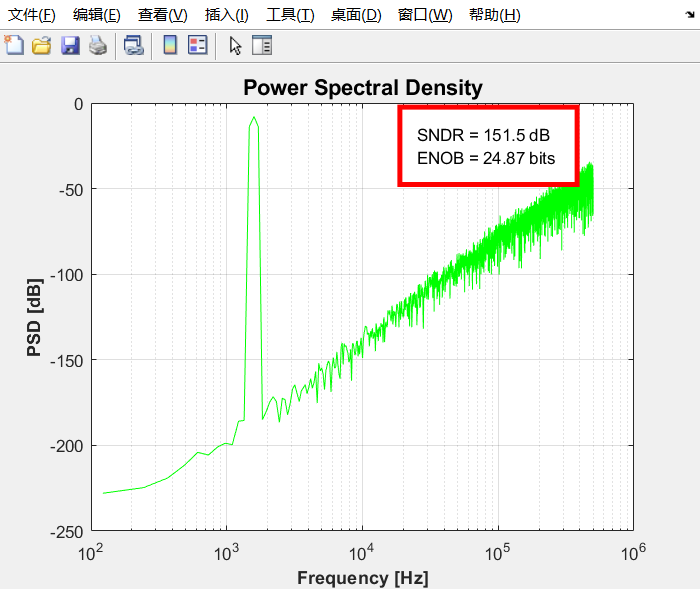
4.1量化器采用SAR结构
将上面代码中的量化器(flash结构)更换为4bit sar结构:
%% sar量化器
w1=[8,4,2,1];
w2=[8,4,2,1];
for p=1:N
x3 = x3 + 3*vi(p) - vfb * 3 + x2 + 3*x1;
x2 = x2 + x1;
x1 =x1 + (vi(p) - vfb);
vres= x3;
dp = 0;
for q = 1:4
if(vres > 0)
d=1;
vres=vres-(w1(q)/sum(w1));
else
d=0;
vres=vres+(w1(q)/sum(w1));
end
dp = dp + d*w2(q);
end
vfb = (dp-Q_dc)/Q_dc;
dout(p) = (dp-Q_dc)/Q_dc;
end
ed_psd(dout',fsig,fclk,128,'g',0)
运行结果:
vin:
dout:
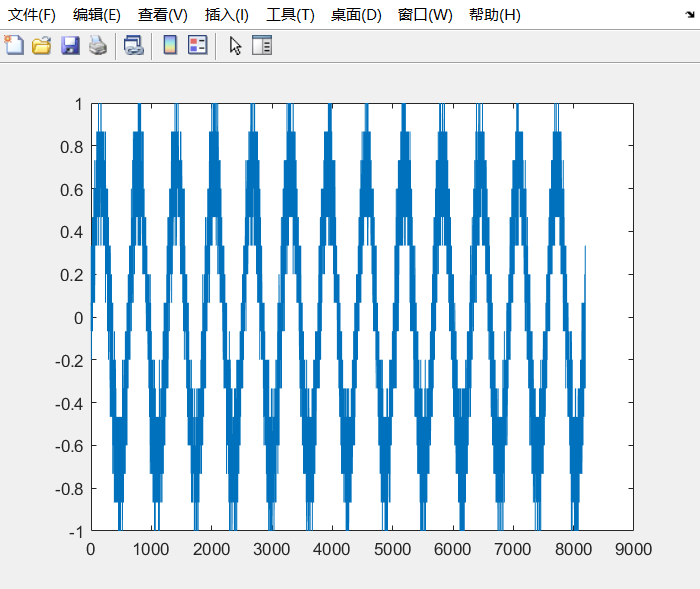
psd:
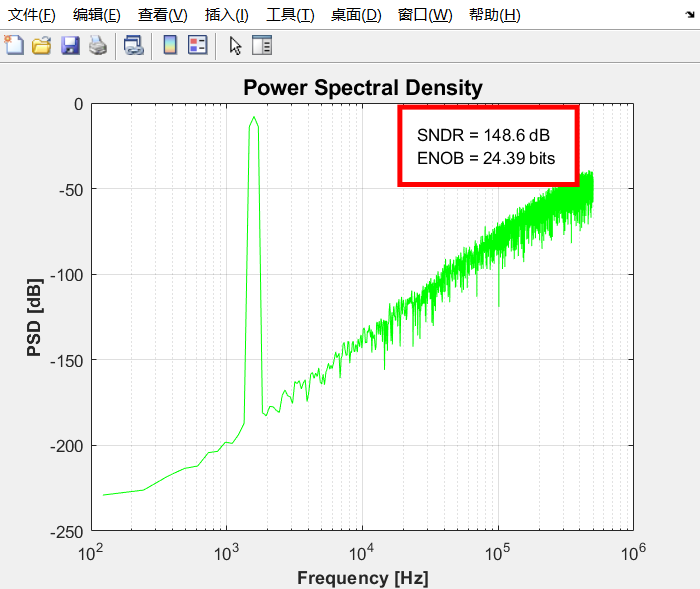
4.2研究反馈DAC电容失配的影响
调整反馈DAC如下:
w1=[7,4,2,1];
w2=[7,4,2,1];
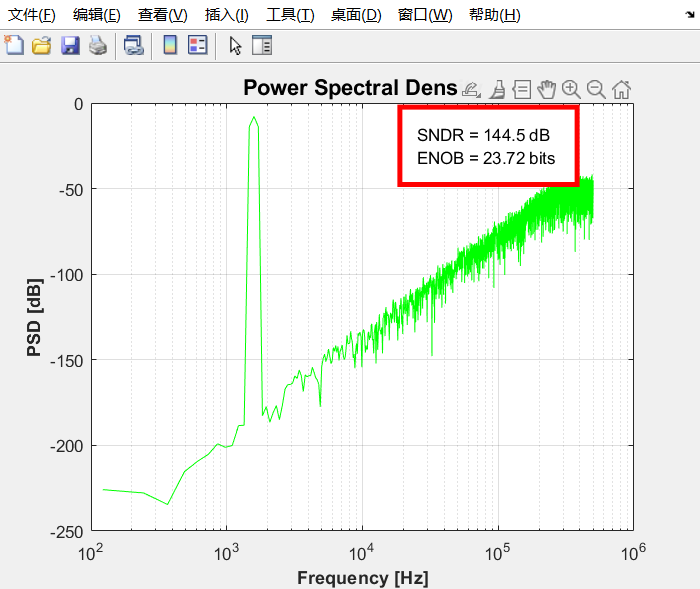
导致SNR产生了4dB的下降
进一步调整DAC如下:
w1=[6,4,2,1];
w2=[6,4,2,1];
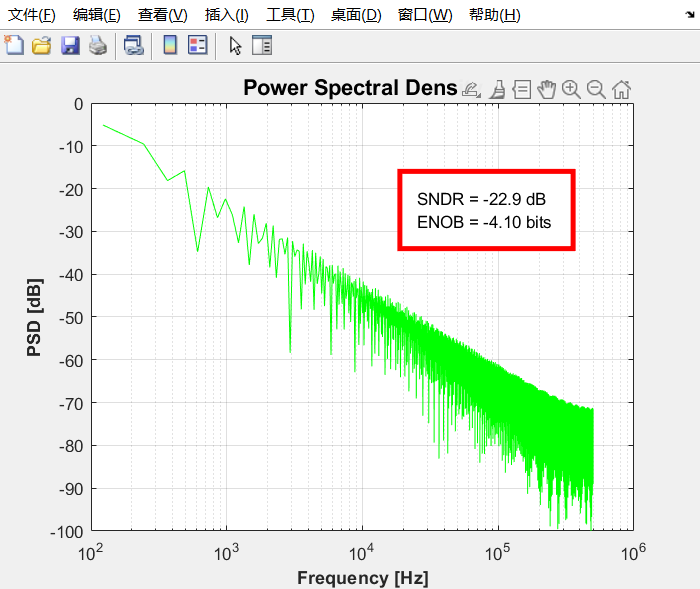
SNR极度下降,ADC无法正常工作
4.3实现动态元件匹配
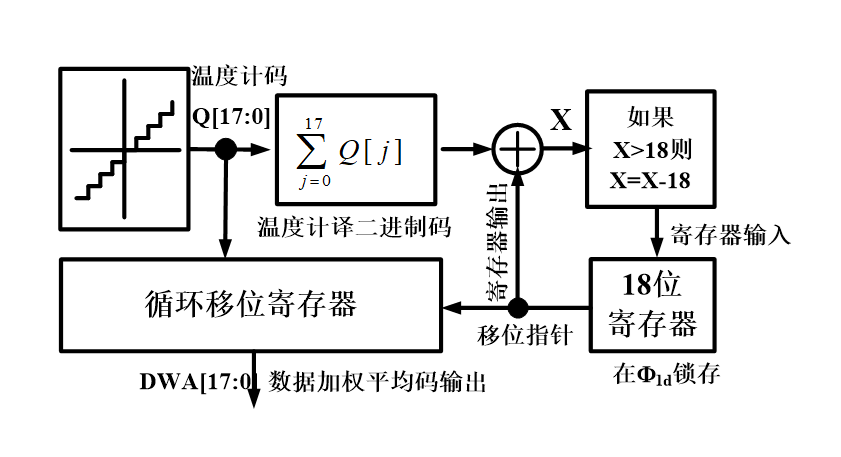
根据原理图进行代码实现:
clear
%% 动态元件匹配
% 位置寄存器值
pos = 0;
% 输入数据总数
N = 4;
% 以16位温度计码格式输入
Q{1} = '0000000011111111';
Q{2} = '0000000011111111';
Q{3} = '0000000011111111';
Q{4} = '0000000011111111';
for i = 1:N
% 温度计码转换为十进制数
Q_dec = sum(Q{i}=='1');
% 更新移位寄存器输出
out{i}=circshift(Q{i}',pos)';
% 更新位置寄存器
pos = Q_dec + pos;
if(pos>16)
pos = pos-16;
end
end
运行结果:

该动态元件匹配因作为DAC的一个子模块,DAC作用于SAR量化器输出,转为模拟反馈电压vfb


