中国科学院大学数字集成电路作业开源——函数运算器章节
中国科学院大学数字集成电路作业开源——第11章
0、说明
第9,10章节分别为高层次综合(HLS)和低功耗设计,没有布置作业,因此接在第8章后就直接是第11章节。
此外,本章节的算法开发与验证需要C/C++和matlab实现的bench,这些内容我放在附录中。
一个经验是,当涉及到这种算法相关的逻辑电路模块开发时,往往需要通过python(一般是神经网络类算法)/ C or C++(语法上与verilog更接近,也更容易转换) / matlab(丰富的内建函数,可以大大简化测试的工作)实现bench,然后再进行逻辑电路的编写。
1、 基于Verilog HDL进行逻辑电路设计
1.1直接频率合成器
设计一个直接频率合成器(DDS)时序逻辑电路,产生可编程的复数单音信号。
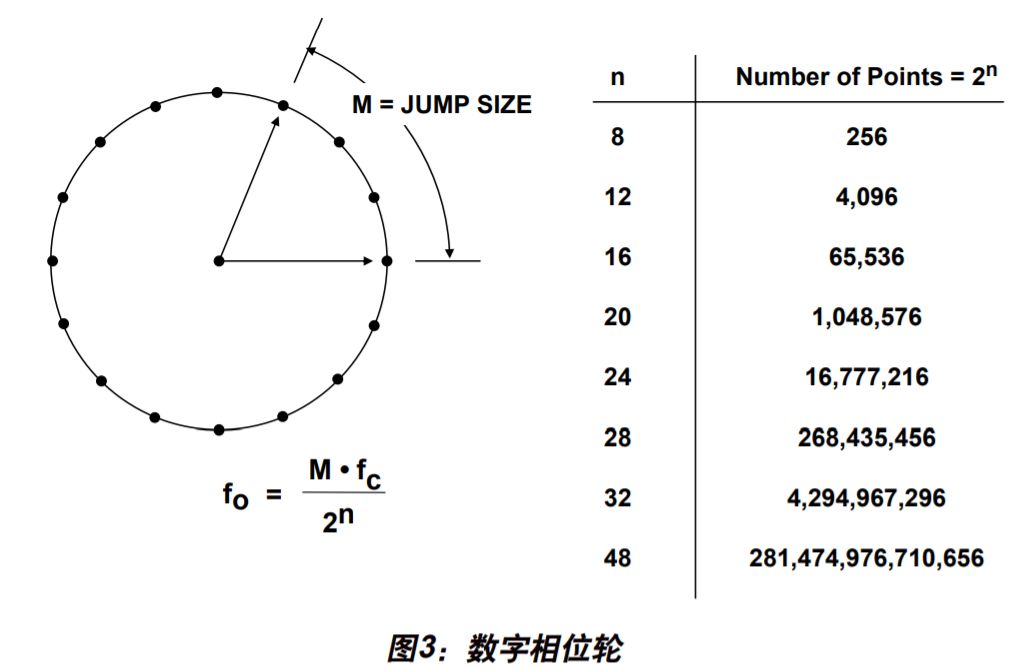
DDS模块的输出频率fout是系统工作频率fclk、相位累加器比特数N以及频率控制字K三者的一个函数,其数学关系式为:
\(f_{out} = f_{clk}/2^N*K\)
对于输入K,计算相位\(theta(n) = K*n\mod2^N\),输出复数单音\(y(n) = exp(2*pi*theta(n)/2^N) = cos(2*pi*(K*n \mod 2^N)/2^N) + j * sin(2*pi*(K*n \mod 2^N)/2N)\),即y的实部为当前相位的余弦、虚部为当前相位的正弦,取值范围为(-1, 1)。
实现时N取20,计算y的实部和虚部使用CORDIC算法旋转模式。模块整体采用流水线结构实现,能够每个时钟周期输出1个有效数据。
顶层模块名为dds,输入输出功能定义:
| 名称 | 方向 | 位宽 | 描述 |
|---|---|---|---|
| clk | I | 1 | 系统时钟 |
| rst_n | I | 1 | 系统异步复位,低电平有效 |
| freq_k | I | 20 | 频率控制字,无符号数,取值范围[1, 220-1] |
| y_re | O | 16 | 输出数据实部,二进制补码定点格式,1位符号整数位,15位小数位,取值范围(-1, 1) |
| y_im | O | 16 | 输出数据虚部,二进制补码定点格式,1位符号整数位,15位小数位,取值范围(-1, 1) |
设计要求:
l Verilog实现代码可综合,给出综合以及仿真结果。
l 对于不同freq_k的输入,能够实时输出对应频率的单音信号。
l 计算过程进行适当精度控制,保证输出结果精确度。
设计思路:
系统拆成两个模块,一个是提供变化的相位角的phase_gen模块,一个是根据相位角计算cos和sin的cordic模块。
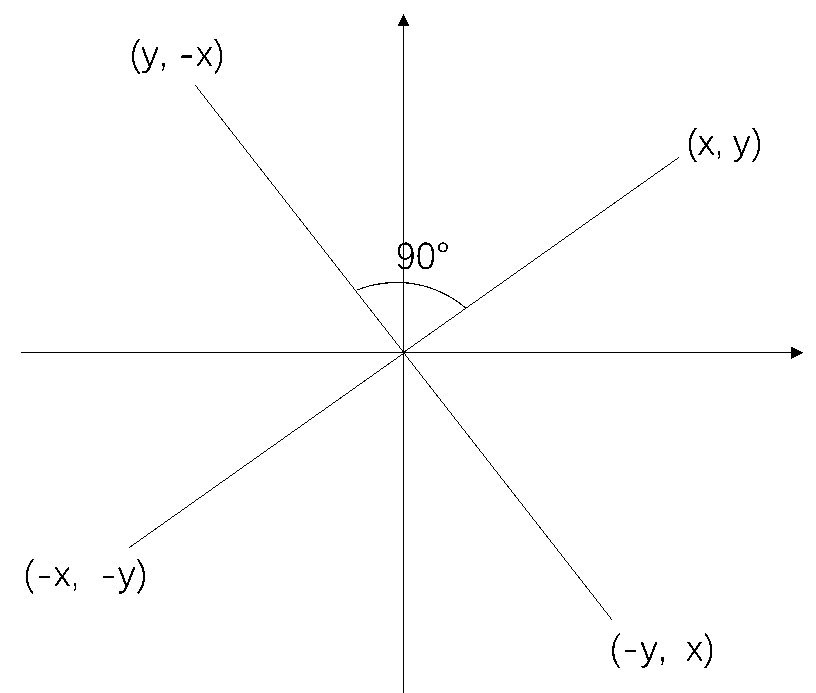
Phase_gen模块在控制累加寄存器,每个clk寄存器值增加freq_k。同时由于cordic算法存在收敛范围的问题,为了能够确保收敛,phase_gen通过一个组合逻辑块将相位角旋转变换到第一象限(0-90°),并记录下相位角原先所在的象限提供给cordic模块。
Cordic模块为流水线结构,共十八级。输出前,根据其原先所在的象限对cordic计算出的x,y进行变换后再输出。
流水线结构的实现借鉴了:https://blog.csdn.net/Reborn_Lee/article/details/87436090
代码实现:
Parameters.v
`ifndef _PARAMETER_H_
`define _PARAMETER_H_
`define PI 3.1415926
// cordic parameters
`define X_ORIGIN 16'sh4dba
`define ANGLE_1 24'sh0c90fd
`define ANGLE_2 24'sh076b19
`define ANGLE_3 24'sh03eb6e
`define ANGLE_4 24'sh01fd5b
`define ANGLE_5 24'sh00ffaa
`define ANGLE_6 24'sh007ff5
`define ANGLE_7 24'sh003ffe
`define ANGLE_8 24'sh001fff
`define ANGLE_9 24'sh000fff
`define ANGLE_10 24'sh0007ff
`define ANGLE_11 24'sh0003ff
`define ANGLE_12 24'sh0001ff
`define ANGLE_13 24'sh0000ff
`define ANGLE_14 24'sh00007f
`define ANGLE_15 24'sh00003f
`define ANGLE_16 24'sh00001f
`define ANGLE_17 24'sh00000f
`define ANGLE_18 24'sh000007
`endif
Phase_gen.v
`include "parameters.v"
module phase_gen (
input clk,
input rst_n,
input [19:0] freq_k,
output [23:0] theta,
output reg [1:0] phase_flag
);
reg [19:0] cnt;
reg [19:0] cnt_post;
always @(posedge clk or negedge rst_n) begin
if(rst_n == 1'b0) begin
cnt <= 0;
end
else begin
cnt <= cnt + freq_k;
end
end
always @(cnt or negedge rst_n) begin
if(rst_n == 1'b0) begin
cnt_post = 0;
phase_flag = 2'b00;
end
else if(cnt < 20'h40000) begin
cnt_post = cnt;
phase_flag = 2'b00;
end
else if(cnt > 20'h40000 && cnt < 20'h80000) begin
cnt_post = cnt - 20'h40000;
phase_flag = 2'b01;
end
else if(cnt > 20'h80000 && cnt < 20'hc0000) begin
cnt_post = cnt - 20'h80000;
phase_flag = 2'b10;
end
else if(cnt > 20'hc0000) begin
cnt_post = cnt - 20'hc0000;
phase_flag = 2'b11;
end
end
// 这里的写法是不可综合的,是我图方便的写法,可综合的实现方法是(2*pi = 6.28318 ≈ 4+2+0.25+0.125)
// 故 theta = (cnt_post << 2) + (cnt_post << 1) + (cnt_post >> 2) + (cnt_post >> 3)
assign theta = `PI * 2 * cnt_post;
endmodule
cordic.v(流水线代码可以通过generate方法生成,这里这样写是受了借鉴的代码的影响,感觉不舒服的可以自己优化)
`include "parameters.v"
module cordic (
input clk,
input rst_n,
input signed [23:0] theta,
input [1:0] phase_flag,
output reg signed [15:0] y_re,
output reg signed [15:0] y_im
);
reg signed [15:0] x_r [18:0];
reg signed [15:0] y_r [18:0];
reg signed [23:0] angle_remain [18:0];
reg [1:0] phase [18:0];
// 初始化
always @(posedge clk or negedge rst_n) begin
if(rst_n == 1'b0) begin
x_r[0] <= 0;
y_r[0] <= 0;
angle_remain[0] <= 0;
end
else begin
x_r[0] <= `X_ORIGIN;
y_r[0] <= 0;
angle_remain[0] <= theta;
end
end
// 流水线第一级
always @(posedge clk) begin
if(rst_n == 1'b0) begin
x_r[1] <= 0;
y_r[1] <= 0;
angle_remain[1] <= 0;
end
else if(angle_remain[0] > 0) begin
x_r[1] <= x_r[0] - y_r[0];
y_r[1] <= y_r[0] + x_r[0];
angle_remain[1] <= angle_remain[0] - `ANGLE_1;
end
else begin
x_r[1] <= x_r[0] + y_r[0];
y_r[1] <= y_r[0] - x_r[0];
angle_remain[1] <= angle_remain[0] + `ANGLE_1;
end
end
// 流水线第二级
always @(posedge clk or negedge rst_n) begin
if(rst_n == 1'b0) begin
x_r[2] <= 0;
y_r[2] <= 0;
angle_remain[2] <= 0;
end
else if(angle_remain[1] > 0) begin
x_r[2] <= x_r[1] - (y_r[1] >>> 1);
y_r[2] <= y_r[1] + (x_r[1] >>> 1);
angle_remain[2] <= angle_remain[1] - `ANGLE_2;
end
else begin
x_r[2] <= x_r[1] + (y_r[1] >>> 1);
y_r[2] <= y_r[1] - (x_r[1] >>> 1);
angle_remain[2] <= angle_remain[1] + `ANGLE_2;
end
end
// 流水线第三级
always @(posedge clk or negedge rst_n) begin
if(rst_n == 1'b0) begin
x_r[3] <= 0;
y_r[3] <= 0;
angle_remain[3] <= 0;
end
else if(angle_remain[2] > 0) begin
x_r[3] <= x_r[2] - (y_r[2] >>> 2);
y_r[3] <= y_r[2] + (x_r[2] >>> 2);
angle_remain[3] <= angle_remain[2] - `ANGLE_3;
end
else begin
x_r[3] <= x_r[2] + (y_r[2] >>> 2);
y_r[3] <= y_r[2] - (x_r[2] >>> 2);
angle_remain[3] <= angle_remain[2] + `ANGLE_3;
end
end
// 流水线第四级
always @(posedge clk or negedge rst_n) begin
if(rst_n == 1'b0) begin
x_r[4] <= 0;
y_r[4] <= 0;
angle_remain[4] <= 0;
end
else if(angle_remain[3] > 0) begin
x_r[4] <= x_r[3] - (y_r[3] >>> 3);
y_r[4] <= y_r[3] + (x_r[3] >>> 3);
angle_remain[4] <= angle_remain[3] - `ANGLE_4;
end
else begin
x_r[4] <= x_r[3] + (y_r[3] >>> 3);
y_r[4] <= y_r[3] - (x_r[3] >>> 3);
angle_remain[4] <= angle_remain[3] + `ANGLE_4;
end
end
// 流水线第五级
always @(posedge clk or negedge rst_n) begin
if(rst_n == 1'b0) begin
x_r[5] <= 0;
y_r[5] <= 0;
angle_remain[5] <= 0;
end
else if(angle_remain[4] > 0) begin
x_r[5] <= x_r[4] - (y_r[4] >>> 4);
y_r[5] <= y_r[4] + (x_r[4] >>> 4);
angle_remain[5] <= angle_remain[4] - `ANGLE_5;
end
else begin
x_r[5] <= x_r[4] + (y_r[4] >>> 4);
y_r[5] <= y_r[4] - (x_r[4] >>> 4);
angle_remain[5] <= angle_remain[4] + `ANGLE_5;
end
end
// 流水线第六级
always @(posedge clk or negedge rst_n) begin
if(rst_n == 1'b0) begin
x_r[6] <= 0;
y_r[6] <= 0;
angle_remain[6] <= 0;
end
else if(angle_remain[5] > 0) begin
x_r[6] <= x_r[5] - (y_r[5] >>> 5);
y_r[6] <= y_r[5] + (x_r[5] >>> 5);
angle_remain[6] <= angle_remain[5] - `ANGLE_6;
end
else begin
x_r[6] <= x_r[5] + (y_r[5] >>> 5);
y_r[6] <= y_r[5] - (x_r[5] >>> 5);
angle_remain[6] <= angle_remain[5] + `ANGLE_6;
end
end
// 流水线第七级
always @(posedge clk or negedge rst_n) begin
if(rst_n == 1'b0) begin
x_r[7] <= 0;
y_r[7] <= 0;
angle_remain[7] <= 0;
end
else if(angle_remain[6] > 0) begin
x_r[7] <= x_r[6] - (y_r[6] >>> 6);
y_r[7] <= y_r[6] + (x_r[6] >>> 6);
angle_remain[7] <= angle_remain[6] - `ANGLE_7;
end
else begin
x_r[7] <= x_r[6] + (y_r[6] >>> 6);
y_r[7] <= y_r[6] - (x_r[6] >>> 6);
angle_remain[7] <= angle_remain[6] + `ANGLE_7;
end
end
// 流水线第八级
always @(posedge clk or negedge rst_n) begin
if(rst_n == 1'b0) begin
x_r[8] <= 0;
y_r[8] <= 0;
angle_remain[8] <= 0;
end
else if(angle_remain[7] > 0) begin
x_r[8] <= x_r[7] - (y_r[7] >>> 7);
y_r[8] <= y_r[7] + (x_r[7] >>> 7);
angle_remain[8] <= angle_remain[7] - `ANGLE_8;
end
else begin
x_r[8] <= x_r[7] + (y_r[7] >>> 7);
y_r[8] <= y_r[7] - (x_r[7] >>> 7);
angle_remain[8] <= angle_remain[7] + `ANGLE_8;
end
end
// 流水线第九级
always @(posedge clk or negedge rst_n) begin
if(rst_n == 1'b0) begin
x_r[9] <= 0;
y_r[9] <= 0;
angle_remain[9] <= 0;
end
else if(angle_remain[8] > 0) begin
x_r[9] <= x_r[8] - (y_r[8] >>> 8);
y_r[9] <= y_r[8] + (x_r[8] >>> 8);
angle_remain[9] <= angle_remain[8] - `ANGLE_9;
end
else begin
x_r[9] <= x_r[8] + (y_r[8] >>> 8);
y_r[9] <= y_r[8] - (x_r[8] >>> 8);
angle_remain[9] <= angle_remain[8] + `ANGLE_9;
end
end
// 流水线第十级
always @(posedge clk or negedge rst_n) begin
if(rst_n == 1'b0) begin
x_r[10] <= 0;
y_r[10] <= 0;
angle_remain[10] <= 0;
end
else if(angle_remain[9] > 0) begin
x_r[10] <= x_r[9] - (y_r[9] >>> 9);
y_r[10] <= y_r[9] + (x_r[9] >>> 9);
angle_remain[10] <= angle_remain[9] - `ANGLE_10;
end
else begin
x_r[10] <= x_r[9] + (y_r[9] >>> 9);
y_r[10] <= y_r[9] - (x_r[9] >>> 9);
angle_remain[10] <= angle_remain[9] + `ANGLE_10;
end
end
// 流水线第十一级
always @(posedge clk or negedge rst_n) begin
if(rst_n == 1'b0) begin
x_r[11] <= 0;
y_r[11] <= 0;
angle_remain[11] <= 0;
end
else if(angle_remain[10] > 0) begin
x_r[11] <= x_r[10] - (y_r[10] >>> 10);
y_r[11] <= y_r[10] + (x_r[10] >>> 10);
angle_remain[11] <= angle_remain[10] - `ANGLE_11;
end
else begin
x_r[11] <= x_r[10] + (y_r[10] >>> 10);
y_r[11] <= y_r[10] - (x_r[10] >>> 10);
angle_remain[11] <= angle_remain[10] + `ANGLE_11;
end
end
// 流水线第十二级
always @(posedge clk or negedge rst_n) begin
if(rst_n == 1'b0) begin
x_r[12] <= 0;
y_r[12] <= 0;
angle_remain[12] <= 0;
end
else if(angle_remain[11] > 0) begin
x_r[12] <= x_r[11] - (y_r[11] >>> 11);
y_r[12] <= y_r[11] + (x_r[11] >>> 11);
angle_remain[12] <= angle_remain[11] - `ANGLE_12;
end
else begin
x_r[12] <= x_r[11] + (y_r[11] >>> 11);
y_r[12] <= y_r[11] - (x_r[11] >>> 11);
angle_remain[12] <= angle_remain[11] + `ANGLE_12;
end
end
// 流水线第十三级
always @(posedge clk or negedge rst_n) begin
if(rst_n == 1'b0) begin
x_r[13] <= 0;
y_r[13] <= 0;
angle_remain[13] <= 0;
end
else if(angle_remain[12] > 0) begin
x_r[13] <= x_r[12] - (y_r[12] >>> 12);
y_r[13] <= y_r[12] + (x_r[12] >>> 12);
angle_remain[13] <= angle_remain[12] - `ANGLE_13;
end
else begin
x_r[13] <= x_r[12] + (y_r[12] >>> 12);
y_r[13] <= y_r[12] - (x_r[12] >>> 12);
angle_remain[13] <= angle_remain[12] + `ANGLE_13;
end
end
// 流水线第十四级
always @(posedge clk or negedge rst_n) begin
if(rst_n == 1'b0) begin
x_r[14] <= 0;
y_r[14] <= 0;
angle_remain[14] <= 0;
end
else if(angle_remain[13] > 0) begin
x_r[14] <= x_r[13] - (y_r[13] >>> 13);
y_r[14] <= y_r[13] + (x_r[13] >>> 13);
angle_remain[14] <= angle_remain[13] - `ANGLE_14;
end
else begin
x_r[14] <= x_r[13] + (y_r[13] >>> 13);
y_r[14] <= y_r[13] - (x_r[13] >>> 13);
angle_remain[14] <= angle_remain[13] + `ANGLE_14;
end
end
// 流水线第十五级
always @(posedge clk or negedge rst_n) begin
if(rst_n == 1'b0) begin
x_r[15] <= 0;
y_r[15] <= 0;
angle_remain[15] <= 0;
end
else if(angle_remain[14] > 0) begin
x_r[15] <= x_r[14] - (y_r[14] >>> 14);
y_r[15] <= y_r[14] + (x_r[14] >>> 14);
angle_remain[15] <= angle_remain[14] - `ANGLE_15;
end
else begin
x_r[15] <= x_r[14] + (y_r[14] >>> 14);
y_r[15] <= y_r[14] - (x_r[14] >>> 14);
angle_remain[15] <= angle_remain[14] + `ANGLE_15;
end
end
// 流水线第十六级
always @(posedge clk or negedge rst_n) begin
if(rst_n == 1'b0) begin
x_r[16] <= 0;
y_r[16] <= 0;
angle_remain[16] <= 0;
end
else if(angle_remain[15] > 0) begin
x_r[16] <= x_r[15] - (y_r[15] >>> 15);
y_r[16] <= y_r[15] + (x_r[15] >>> 15);
angle_remain[16] <= angle_remain[15] - `ANGLE_16;
end
else begin
x_r[16] <= x_r[15] + (y_r[15] >>> 15);
y_r[16] <= y_r[15] - (x_r[15] >>> 15);
angle_remain[16] <= angle_remain[15] + `ANGLE_16;
end
end
// 流水线第十七级
always @(posedge clk or negedge rst_n) begin
if(rst_n == 1'b0) begin
x_r[17] <= 0;
y_r[17] <= 0;
angle_remain[17] <= 0;
end
else if(angle_remain[16] > 0) begin
x_r[17] <= x_r[16] - (y_r[16] >>> 16);
y_r[17] <= y_r[16] + (x_r[16] >>> 16);
angle_remain[17] <= angle_remain[16] - `ANGLE_17;
end
else begin
x_r[17] <= x_r[16] + (y_r[16] >>> 16);
y_r[17] <= y_r[16] - (x_r[16] >>> 16);
angle_remain[17] <= angle_remain[16] + `ANGLE_17;
end
end
// 流水线第十八级
always @(posedge clk or negedge rst_n) begin
if(rst_n == 1'b0) begin
x_r[18] <= 0;
y_r[18] <= 0;
angle_remain[18] <= 0;
end
else if(angle_remain[17] > 0) begin
x_r[18] <= x_r[17] - (y_r[17] >>> 17);
y_r[18] <= y_r[17] + (x_r[17] >>> 17);
angle_remain[18] <= angle_remain[17] - `ANGLE_18;
end
else begin
x_r[18] <= x_r[17] + (y_r[17] >>> 17);
y_r[18] <= y_r[17] - (x_r[17] >>> 17);
angle_remain[18] <= angle_remain[17] + `ANGLE_18;
end
end
always @(posedge clk or negedge rst_n) begin
if(rst_n == 1'b0) begin
phase[0] <= 0;
phase[1] <= 0;
phase[2] <= 0;
phase[3] <= 0;
phase[4] <= 0;
phase[5] <= 0;
phase[6] <= 0;
phase[7] <= 0;
phase[8] <= 0;
phase[9] <= 0;
phase[10] <= 0;
phase[11] <= 0;
phase[12] <= 0;
phase[13] <= 0;
phase[14] <= 0;
phase[15] <= 0;
phase[16] <= 0;
phase[17] <= 0;
phase[18] <= 0;
end
else begin
phase[0] <= phase_flag;
phase[1] <= phase[0];
phase[2] <= phase[1];
phase[3] <= phase[2];
phase[4] <= phase[3];
phase[5] <= phase[4];
phase[6] <= phase[5];
phase[7] <= phase[6];
phase[8] <= phase[7];
phase[9] <= phase[8];
phase[10] <= phase[9];
phase[11] <= phase[10];
phase[12] <= phase[11];
phase[13] <= phase[12];
phase[14] <= phase[13];
phase[15] <= phase[14];
phase[16] <= phase[15];
phase[17] <= phase[16];
phase[18] <= phase[17];
end
end
always @(*) begin
case(phase[18])
2'b00: begin
y_re = x_r[18];
y_im = y_r[18];
end
2'b01: begin
y_re = ~y_r[18] + 1;
y_im = x_r[18];
end
2'b10: begin
y_re = ~x_r[18] + 1;
y_im = ~y_r[18] + 1;
end
2'b11: begin
y_re = y_r[18];
y_im = ~x_r[18] + 1;
end
default: begin
y_re = x_r[18];
y_im = y_r[18];
end
endcase
end
endmodule
testbench.v
module testbench ();
reg clk;
reg rst_n;
reg [19:0] freq_k;
wire [15:0] y_re;
wire [15:0] y_im;
initial begin
clk <= 1'b0;
rst_n <= 1'b0;
freq_k <= 83886;
#20
rst_n <= 1'b1;
end
always #10 clk <= ~clk;
dds u1(
.clk(clk),
.rst_n(rst_n),
.freq_k(freq_k),
.y_re(y_re),
.y_im(y_im)
);
endmodule
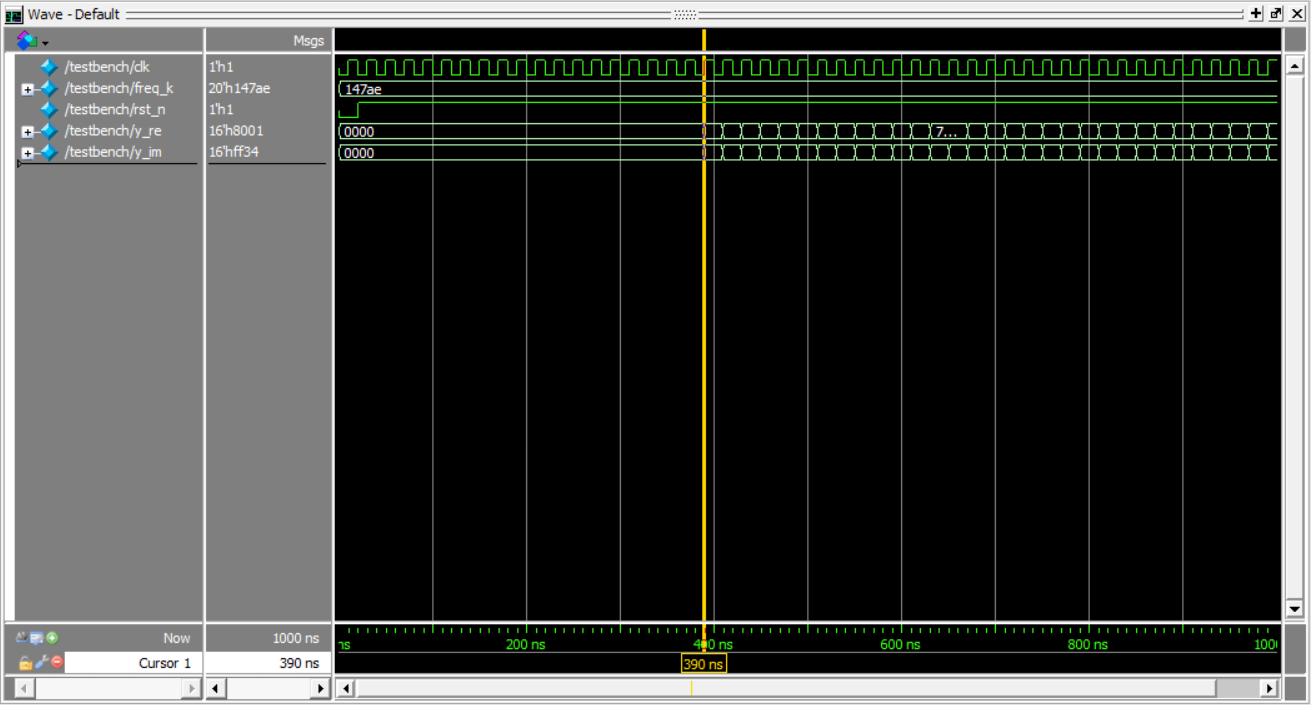
仿真结果:
cordic流水线工作情况,前18拍装填流水线,装满后每拍输出一个结果。
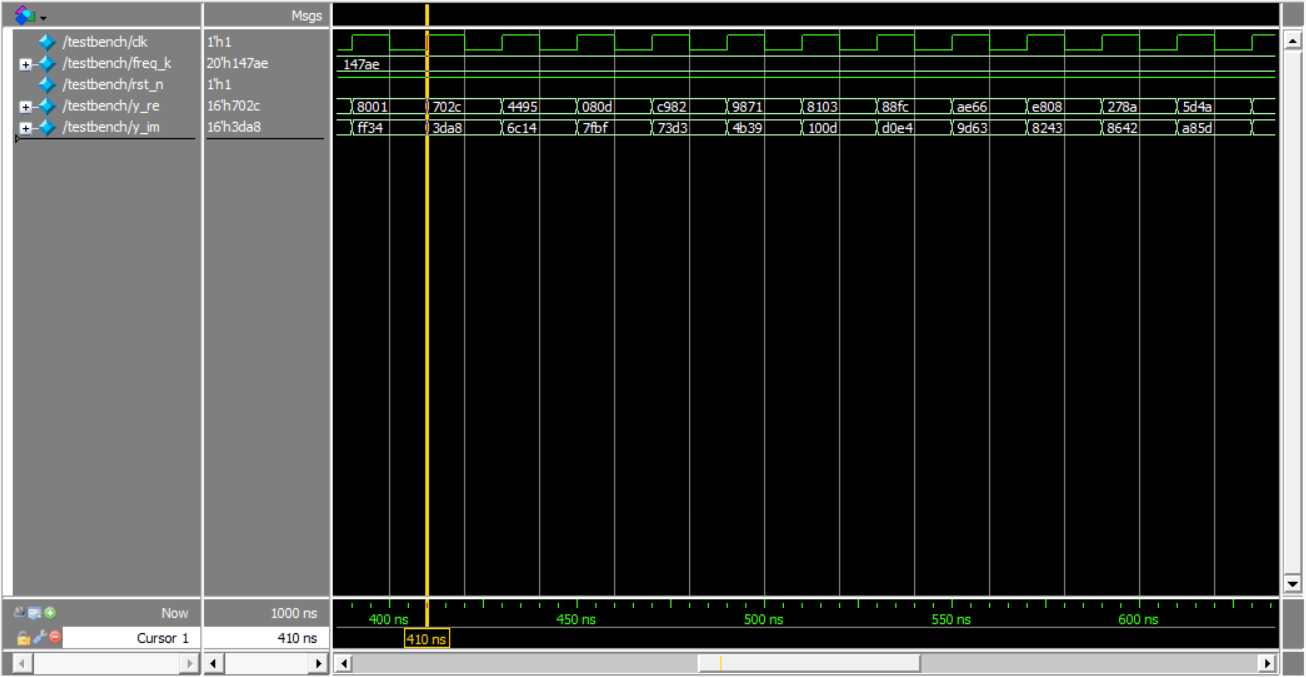
输出的y_re,y_im二进制补码定点格式,1位符号整数位,15位小数位,取值范围(-1, 1)。对于符号位为0的数,将其除以\(2^{15}\)得到其小数表示,例如:
702c -> 0.876343
3da8 -> 0.481689
4495 -> 0.535797
对于符号位为1的数,将其减去\(2^{16}\)后再除以\(2^{15}\)得到小数表示,例如
c982 -> -0.42572
9871 -> -0.809052
8103 -> -0.992096
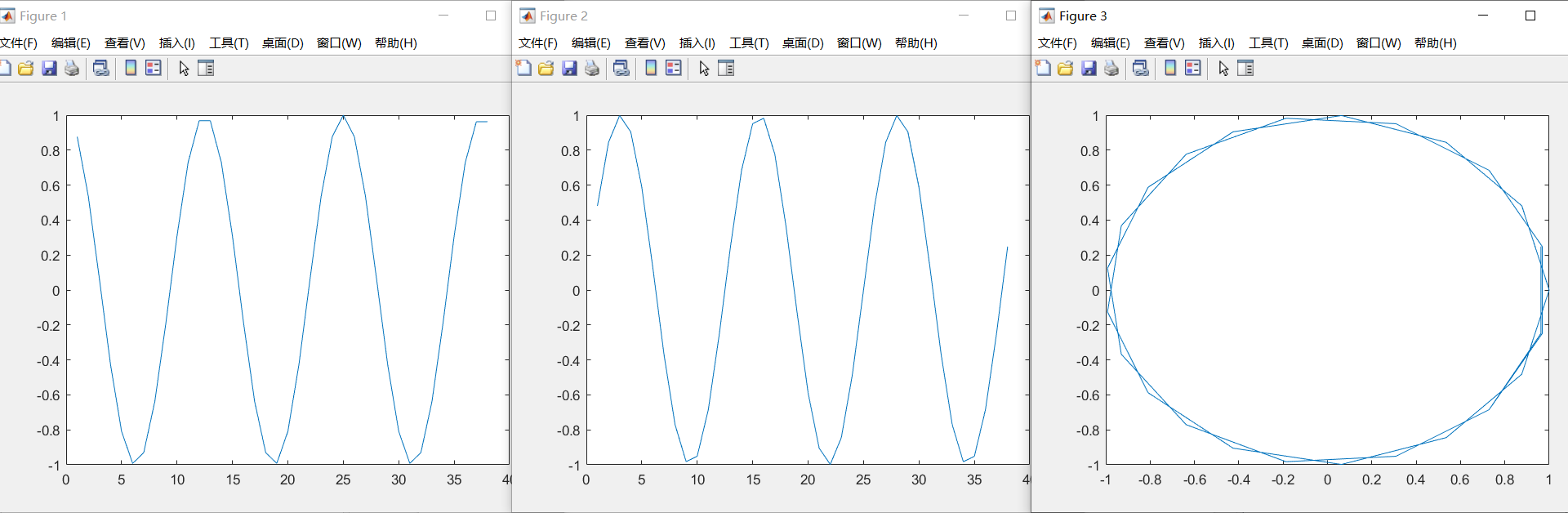
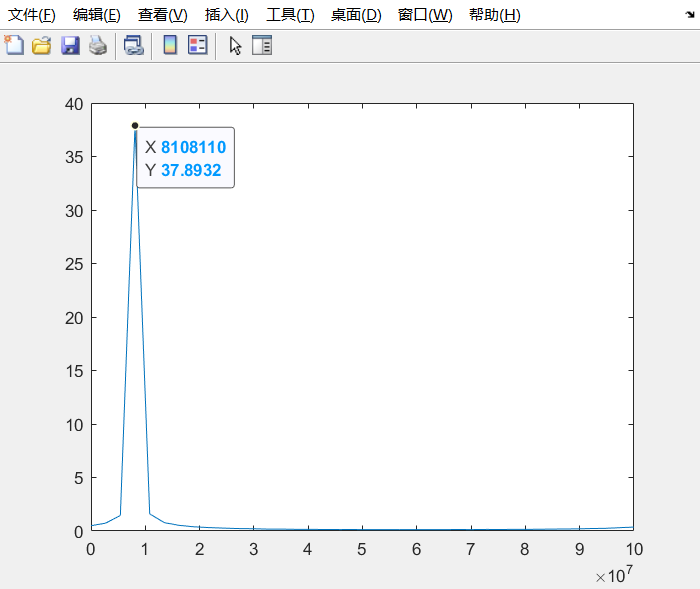
将以上结果导出到matlab中,三张图分别为y_re,y_im,(y_re,y_im)
进行fft得到频谱,对于freq_k设置为85536,假设时钟频率为100Mhz的dds,其输出的单音信号的频谱为频点在8Mhz的尖峰(这里只导出了38个点,用更多的点求fft能更准确):
附录:
Cordic.cpp
#include <iostream>
#include <cmath>
#include <math.h>
using namespace std;
static const double g_product_cos_table[64] = {
7.071067811865475E-1, 6.324555320336759E-1, 6.135719910778963E-1, 6.088339125177524E-1,
6.076482562561681E-1, 6.073517701412958E-1, 6.072776440935258E-1, 6.072591122988925E-1,
6.07254479332562E-1, 6.072533210898748E-1, 6.072530315291339E-1, 6.072529591389442E-1,
6.072529410413965E-1, 6.072529365170094E-1, 6.072529353859126E-1, 6.072529351031383E-1,
6.072529350324446E-1, 6.072529350147711E-1, 6.072529350103526E-1, 6.072529350092478E-1,
6.072529350089715E-1, 6.072529350089023E-1, 6.072529350088848E-1, 6.072529350088803E-1,
6.072529350088791E-1, 6.072529350088786E-1, 6.072529350088783E-1, 6.072529350088781E-1,
6.072529350088778E-1, 6.072529350088776E-1, 6.072529350088773E-1, 6.072529350088771E-1,
6.072529350088768E-1, 6.072529350088765E-1, 6.072529350088762E-1, 6.072529350088759E-1,
6.072529350088756E-1, 6.072529350088753E-1, 6.07252935008875E-1, 6.072529350088746E-1,
6.072529350088743E-1, 6.07252935008874E-1, 6.072529350088736E-1, 6.072529350088733E-1,
6.072529350088729E-1, 6.072529350088725E-1, 6.072529350088721E-1, 6.072529350088717E-1,
6.072529350088713E-1, 6.072529350088709E-1, 6.072529350088705E-1, 6.0725293500887E-1,
6.072529350088696E-1, 6.072529350088692E-1, 6.072529350088687E-1, 6.072529350088683E-1,
6.072529350088678E-1, 6.072529350088673E-1, 6.072529350088668E-1, 6.072529350088663E-1,
6.072529350088658E-1, 6.072529350088653E-1, 6.072529350088648E-1, 6.072529350088642E-1
};
/* g_atan_table[i] = atan(2^-i). when i >= 25 abs((atan(2^-i)-2^-i)/atan(2^-i)) < 1E-15. */
static const double g_atan_table[64] = {
7.853981633974483E-1, 4.636476090008061E-1, 2.449786631268642E-1, 1.243549945467614E-1,
6.241880999595735E-2, 3.123983343026828E-2, 1.562372862047683E-2, 7.812341060101111E-3,
3.906230131966972E-3, 1.953122516478819E-3, 9.765621895593194E-4, 4.882812111948983E-4,
2.441406201493618E-4, 1.220703118936702E-4, 6.103515617420878E-5, 3.05175781155261E-5,
1.525878906131576E-5, 7.62939453110197E-6, 3.814697265606496E-6, 1.907348632810187E-6,
9.536743164059609E-7, 4.768371582030889E-7, 2.38418579101558E-7, 1.192092895507807E-7,
5.960464477539055E-8, 2.98023223876953E-8, 1.490116119384766E-8, 7.450580596923828E-9,
3.725290298461914E-9, 1.862645149230957E-9, 9.313225746154785E-10, 4.656612873077393E-10,
2.328306436538696E-10, 1.164153218269348E-10, 5.820766091346741E-11, 2.91038304567337E-11,
1.455191522836685E-11, 7.275957614183426E-12, 3.637978807091713E-12, 1.818989403545856E-12,
9.094947017729282E-13, 4.547473508864641E-13, 2.273736754432321E-13, 1.13686837721616E-13,
5.684341886080801E-14, 2.842170943040401E-14, 1.4210854715202E-14, 7.105427357601002E-15,
3.552713678800501E-15, 1.77635683940025E-15, 8.881784197001252E-16, 4.440892098500626E-16,
2.220446049250313E-16, 1.110223024625157E-16, 5.551115123125783E-17, 2.775557561562891E-17,
1.387778780781446E-17, 6.938893903907228E-18, 3.469446951953614E-18, 1.734723475976807E-18,
8.673617379884035E-19, 4.336808689942018E-19, 2.168404344971009E-19, 1.084202172485504E-19
};
double my_cos(const double t) {
const int n = 18 ;
double x = g_product_cos_table[n - 1];
double xt;
double y = 0.0;
double z = 0.0;
double k = 1.0;
int i;
if (t < 0 || t > M_PI / 2) {
return 0.0;
}
for (i = 0; i < n; i++) {
xt = x;
if (t > z) {
x = x - y * k;
y = y + xt * k;
z = z + g_atan_table[i];
} else {
x = x + y * k;
y = y - xt * k;
z = z - g_atan_table[i];
}
k *= 0.5;
/*
cout << "第" << i << "次旋转" << endl;
cout << "x = " << x << endl;
cout << "y = " << y << endl;
cout << "angle = " << z << endl;
*/
}
return x;
}
/* return sin(t) */
double my_sin(const double t) {
const int n = 18;
double x = g_product_cos_table[n - 1];
double xt;
double y = 0.0;
double z = 0.0;
double k = 1.0;
int i;
if (t < 0 || t > M_PI / 2) {
return 0.0;
}
for (i = 0; i < n; i++) {
xt = x;
if (t > z) {
x = x - y * k;
y = y + xt * k;
z = z + g_atan_table[i];
} else {
x = x + y * k;
y = y - xt * k;
z = z - g_atan_table[i];
}
k *= 0.5;
}
return y;
}
int main(void) {
double x;
cin >> x;
long long int sum;
long long int sum_post;
int phase_flag;
double phase;
sum = 0;
for (int i = 0; i < x - 1; i++) {
sum += 83886;
if (sum > pow(2, 20)) {
sum = sum % 1048576;
}
if (sum < 262144) {
sum_post = sum;
phase_flag = 0;
} else if (sum >= 262144 && sum < 524288) {
sum_post = sum - 262144;
phase_flag = 1;
} else if (sum >= 524288 && sum < 786432) {
sum_post = sum - 524288;
phase_flag = 2;
} else {
sum_post = sum - 786432;
phase_flag = 3;
}
phase = sum_post * 2 * M_PI / pow(2, 20);
cout << "sum_post = " << sum_post << endl;
cout << "angle = " << sum * 360 / pow(2, 20) << endl;
switch (phase_flag) {
case 0:
cout << "cos(phase) = " << my_cos(phase) << endl;
cout << "sin(phase) = " << my_sin(phase) << endl;
break;
case 1:
cout << "cos(phase) = " << -1 * my_sin(phase) << endl;
cout << "sin(phase) = " << my_cos(phase) << endl;
break;
case 2:
cout << "cos(phase) = " << -1 * my_cos(phase) << endl;
cout << "sin(phase) = " << -1 * my_sin(phase) << endl;
break;
case 3:
cout << "cos(phase) = " << my_sin(phase) << endl;
cout << "sin(phase) = " << -1 * my_cos(phase) << endl;
}
}
}
Hex2dec.cpp
#include <iostream>
#include <cmath>
using namespace std;
long fun(char *s) {
int i, t; //t记录临时加的数
long sum = 0;
for (i = 0; s[i]; i++) {
if (s[i] >= '0' && s[i] <= '9')
t = s[i] - '0'; //当字符是0~9时保持原数不变
if (s[i] >= 'a' && s[i] <= 'z')
t = s[i] - 'a' + 10;
if (s[i] >= 'A' && s[i] <= 'Z')
t = s[i] - 'A' + 10;
sum = sum * 16 + t;
}
if (s[0] < '8') {
sum = sum;
} else {
sum = sum - pow(2, 16);
}
return sum;
}
int main(void) {
char input[4];
while (input[0] != 'q') {
cin >> input;
cout << fun(input) / pow(2, 15) << endl;
}
return 0;
}
test.m
x = [0.876343, 0.535797, 0.0628967, -0.42572, -0.809052, -0.992096, -0.92981, -0.637512, -0.187256, 0.308899, 0.728821, 0.968628, 0.968628, 0.728943, 0.308899, -0.187256, -0.637451, -0.92981, -0.992096, -0.809052, -0.42572, 0.0628967, 0.535797, 0.876343, 1, 0.876343, 0.535797, 0.0628967, -0.42572, -0.809052, -0.992096, -0.92981, -0.637512, -0.1875, 0.308899, 0.728821, 0.962628, 0.962628];
y = [0.481689, 0.84436, 0.998016, 0.904877, 0.587677, 0.125397, -0.368042, -0.770416, -0.98233, -0.951111, -0.684662, -0.248657, 0.248657, 0.68454, 0.951111, 0.98233, 0.776477, 0.368042, -0.125336, -0.587677, -0.904877, -0.998016, -0.84436, -0.481689, 0, 0.481689, 0.84436, 0.998016, 0.904877, 0.587677, 0.125397, -0.368042, -0.770416, -0.982269, -0.951111, -0.684662, -0.248657, 0.248657];
figure(1)
plot(t,x);
figure(2)
plot(t,y)
figure(3)
plot(x,y)
fs = 100000000;
f = fs*(0:37)/37;
z = x + 1i * y;
z_f = fft(z);
figure(4)
plot(f,abs(z_f));
1.2复数相位角计算
设计一个时序逻辑电路,对输入复数Z = X + Y*i,计算其归一化相位角P(取值范围[-1, 1))。例如:
l Z = 10 +10i, P = 0.25
l Z = -3 + 4i,P = 0.704833
l Z = 3 – 4i,P = -0.295167
l Z = -10 + 0i, P = -1
计算相角使用CORDIC算法向量模式。模块采用串行结构实现,对于每个有效输入,经过若干时钟周期能够输出1个有效数据。
顶层模块名为calc_phase,输入输出功能定义:
| 名称 | 方向 | 位宽 | 描述 |
|---|---|---|---|
| clk | I | 1 | 系统时钟 |
| rst_n | I | 1 | 系统异步复位,低电平有效 |
| vld_in | I | 1 | 输入数据有效指示 |
| x | I | 16 | 输入实部数据,二进制补码格式 |
| y | I | 16 | 输入虚部数据,二进制补码格式 |
| vld_out | O | 1 | 输出数据有效指示 |
| p | O | 16 | 输出相位数据,二进制补码定点格式,1位符号整数位,15位小数位,取值范围[-1, 1) |
设计要求:
l Verilog实现代码可综合,给出综合以及仿真结果。
l 计算过程进行适当精度控制,保证输出结果精确度。
设计思路:
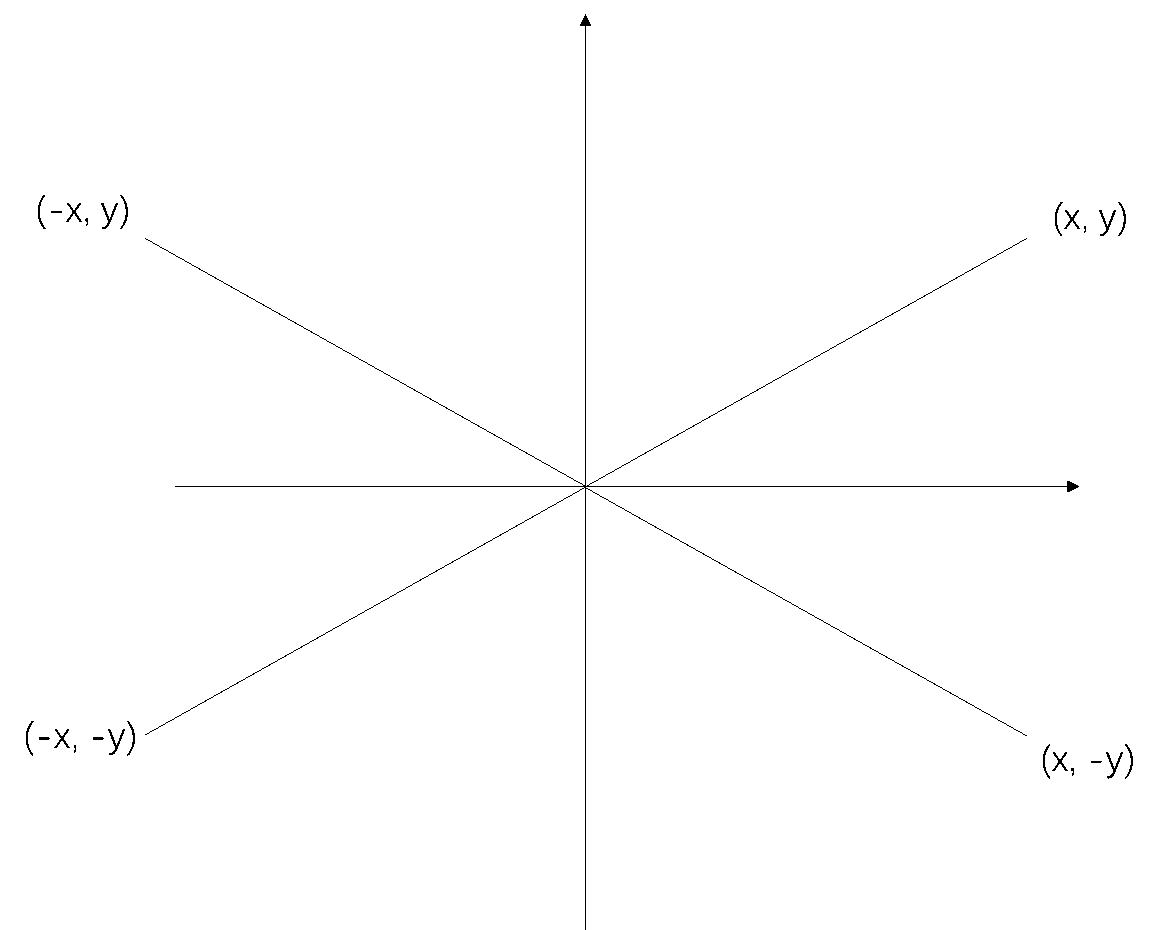
首先对输入向量进行处理,记录其原先所在象限并统一变换到第一象限,避免cordic算法不收敛或错误收敛。
Cordic算法采用串行结构,由cnt计数器控制cordic算法的数据通路,实现迭代运算,所消耗的寄存器数量远远小于流水线结构。Cordic输出前根据输入向量原先所在象限对输入进行处理。另外由于输入是没有小数位的,在计算cordic时会由于精度不足导致较大的误差,因此为其拓展了10位的小数精度。
代码实现:
Parameters.v
`ifndef _PARAMETER_H_
`define _PARAMETER_H_
`define INV_PI 0.3183099
`define ANGLE_1 16'sh6487
`define ANGLE_2 16'sh3b58
`define ANGLE_3 16'sh1f5b
`define ANGLE_4 16'sh0fea
`define ANGLE_5 16'sh07fd
`define ANGLE_6 16'sh03ff
`define ANGLE_7 16'sh01ff
`define ANGLE_8 16'sh00ff
`define ANGLE_9 16'sh007f
`define ANGLE_10 16'sh003f
`define ANGLE_11 16'sh001f
`define ANGLE_12 16'sh000f
`define ANGLE_13 16'sh0007
`define ANGLE_14 16'sh0003
`define ANGLE_15 16'sh0001
`endif
Input_process.v
module input_process (
input signed [15:0] x,
input signed [15:0] y,
input vld_in,
output signed [15:0] x_out,
output signed [15:0] y_out,
output reg [2:0] phase_flag
);
reg signed [15:0] x_post;
reg signed [15:0] y_post;
always @(*) begin
if (x > 0 && y > 0) begin
x_post = x;
y_post = y;
phase_flag = 3'b000;
end
else if (x < 0 && y > 0) begin
x_post = ~x + 1;
y_post = y;
phase_flag = 3'b001;
end
else if (x < 0 && y < 0) begin
x_post = ~x + 1;
y_post = ~y + 1;
phase_flag = 3'b010;
end
else if (x > 0 && y < 0) begin
x_post = x;
y_post = ~y + 1;
phase_flag = 3'b011;
end
else if (x > 0 && y == 0) begin
x_post = x;
y_post = y;
phase_flag = 3'b100;
end
else if (x == 0 && y > 0) begin
x_post = x;
y_post = y;
phase_flag = 3'b101;
end
else if (x < 0 && y == 0) begin
x_post = x;
y_post = y;
phase_flag = 3'b110;
end
else if (x == 0 && y < 0) begin
x_post = x;
y_post = y;
phase_flag = 3'b111;
end
end
assign x_out = x_post & {16{vld_in}};
assign y_out = y_post & {16{vld_in}};
endmodule
cordic.v
`include "parameters.v"
module cordic (
input clk,
input rst_n,
input signed [15:0] x,
input signed [15:0] y,
input [2:0] phase_flag,
output reg vld_out,
output reg signed [15:0] p
);
reg [3:0] cnt;
reg signed [25:0] x_pre,x_post;
reg signed [25:0] y_post;
reg [15:0] angle_remain;
always @(posedge clk or negedge rst_n) begin
if(rst_n == 1'b0) begin
cnt <= 0;
end
else begin
cnt <= cnt + 1;
end
end
always @(*) begin
case(cnt)
4'b0000: begin
x_pre = 0;
x_post = {x,10'b0};
y_post = {y,10'b0};
angle_remain = 0;
vld_out = 1'b0;
end
4'b0001: begin
if(y_post > 0) begin
x_pre = x_post;
x_post = x_post + y_post;
y_post = y_post - x_pre;
angle_remain = angle_remain + `ANGLE_1;
end
else begin
x_pre = x_post;
x_post = x_post - y_post;
y_post = y_post + x_pre;
angle_remain = angle_remain - `ANGLE_1;
end
end
4'b0010: begin
if(y_post > 0) begin
x_pre = x_post;
x_post = x_post + (y_post >>> 1);
y_post = y_post - (x_pre >>> 1);
angle_remain = angle_remain + `ANGLE_2;
end
else begin
x_pre = x_post;
x_post = x_post - (y_post >>> 1);
y_post = y_post + (x_pre >>> 1);
angle_remain = angle_remain - `ANGLE_2;
end
end
4'b0011: begin
if(y_post > 0) begin
x_pre = x_post;
x_post = x_post + (y_post >>> 2);
y_post = y_post - (x_pre >>> 2);
angle_remain = angle_remain + `ANGLE_3;
end
else begin
x_pre = x_post;
x_post = x_post - (y_post >>> 2);
y_post = y_post + (x_pre >>> 2);
angle_remain = angle_remain - `ANGLE_3;
end
end
4'b0100: begin
if(y_post > 0) begin
x_pre = x_post;
x_post = x_post + (y_post >>> 3);
y_post = y_post - (x_pre >>> 3);
angle_remain = angle_remain + `ANGLE_4;
end
else begin
x_pre = x_post;
x_post = x_post - (y_post >>> 3);
y_post = y_post + (x_pre >>> 3);
angle_remain = angle_remain - `ANGLE_4;
end
end
4'b0101: begin
if(y_post > 0) begin
x_pre = x_post;
x_post = x_post + (y_post >>> 4);
y_post = y_post - (x_pre >>> 4);
angle_remain = angle_remain + `ANGLE_5;
end
else begin
x_pre = x_post;
x_post = x_post - (y_post >>> 4);
y_post = y_post + (x_pre >>> 4);
angle_remain = angle_remain - `ANGLE_5;
end
end
4'b0110: begin
if(y_post > 0) begin
x_pre = x_post;
x_post = x_post + (y_post >>> 5);
y_post = y_post - (x_pre >>> 5);
angle_remain = angle_remain + `ANGLE_6;
end
else begin
x_pre = x_post;
x_post = x_post - (y_post >>> 5);
y_post = y_post + (x_pre >>> 5);
angle_remain = angle_remain - `ANGLE_6;
end
end
4'b0111: begin
if(y_post > 0) begin
x_pre = x_post;
x_post = x_post + (y_post >>> 6);
y_post = y_post - (x_pre >>> 6);
angle_remain = angle_remain + `ANGLE_7;
end
else begin
x_pre = x_post;
x_post = x_post - (y_post >>> 6);
y_post = y_post + (x_pre >>> 6);
angle_remain = angle_remain - `ANGLE_7;
end
end
4'b1000: begin
if(y_post > 0) begin
x_pre = x_post;
x_post = x_post + (y_post >>> 7);
y_post = y_post - (x_pre >>> 7);
angle_remain = angle_remain + `ANGLE_8;
end
else begin
x_pre = x_post;
x_post = x_post - (y_post >>> 7);
y_post = y_post + (x_pre >>> 7);
angle_remain = angle_remain - `ANGLE_8;
end
end
4'b1001: begin
if(y_post > 0) begin
x_pre = x_post;
x_post = x_post + (y_post >>> 8);
y_post = y_post - (x_pre >>> 8);
angle_remain = angle_remain + `ANGLE_9;
end
else begin
x_pre = x_post;
x_post = x_post - (y_post >>> 8);
y_post = y_post + (x_pre >>> 8);
angle_remain = angle_remain - `ANGLE_9;
end
end
4'b1010: begin
if(y_post > 0) begin
x_pre = x_post;
x_post = x_post + (y_post >>> 9);
y_post = y_post - (x_pre >>> 9);
angle_remain = angle_remain + `ANGLE_10;
end
else begin
x_pre = x_post;
x_post = x_post - (y_post >>> 9);
y_post = y_post + (x_pre >>> 9);
angle_remain = angle_remain - `ANGLE_10;
end
end
4'b1011: begin
if(y_post > 0) begin
x_pre = x_post;
x_post = x_post + (y_post >>> 10);
y_post = y_post - (x_pre >>> 10);
angle_remain = angle_remain + `ANGLE_11;
end
else begin
x_pre = x_post;
x_post = x_post - (y_post >>> 10);
y_post = y_post + (x_pre >>> 10);
angle_remain = angle_remain - `ANGLE_11;
end
end
4'b1100: begin
if(y_post > 0) begin
x_pre = x_post;
x_post = x_post + (y_post >>> 11);
y_post = y_post - (x_pre >>> 11);
angle_remain = angle_remain + `ANGLE_12;
end
else begin
x_pre = x_post;
x_post = x_post - (y_post >>> 11);
y_post = y_post + (x_pre >>> 11);
angle_remain = angle_remain - `ANGLE_12;
end
end
4'b1101: begin
if(y_post > 0) begin
x_pre = x_post;
x_post = x_post + (y_post >>> 12);
y_post = y_post - (x_pre >>> 12);
angle_remain = angle_remain + `ANGLE_13;
end
else begin
x_pre = x_post;
x_post = x_post - (y_post >>> 12);
y_post = y_post + (x_pre >>> 12);
angle_remain = angle_remain - `ANGLE_13;
end
end
4'b1110: begin
if(y_post > 0) begin
x_pre = x_post;
x_post = x_post + (y_post >>> 13);
y_post = y_post - (x_pre >>> 13);
angle_remain = angle_remain + `ANGLE_14;
end
else begin
x_pre = x_post;
x_post = x_post - (y_post >>> 13);
y_post = y_post + (x_pre >>> 13);
angle_remain = angle_remain - `ANGLE_14;
end
end
4'b1111: begin
if(y_post > 0) begin
x_pre = x_post;
x_post = x_post + (y_post >>> 14);
y_post = y_post - (x_pre >>> 14);
angle_remain = angle_remain + `ANGLE_15;
vld_out = 1'b1;
end
else begin
x_pre = x_post;
x_post = x_post - (y_post >>> 14);
y_post = y_post + (x_pre >>> 14);
angle_remain = angle_remain - `ANGLE_15;
vld_out = 1'b1;
end
end
endcase
end
// 这里 * `INV_PI的写法同样是不可综合的,应使用和上一题一样的方法用移位相加来替代
always @(*) begin
if (vld_out == 1'b1) begin
case(phase_flag)
3'b000: begin
p = angle_remain * `INV_PI;
end
3'b001: begin
p = 16'sh7fff - angle_remain * `INV_PI;
end
3'b010: begin
p = 16'sh8000 + angle_remain * `INV_PI;
end
3'b011: begin
p = angle_remain * `INV_PI;
p = ~p + 16'sh0001;
end
3'b100: begin
p = 0;
end
3'b101: begin
p = 16'sh4000;
end
3'b110: begin
p = 16'sh8000;
end
3'b111: begin
p = 16'shc000;
end
endcase
end
else begin
p = 0;
end
end
endmodule
calc_phase.v
module calc_phase (
input clk,
input rst_n,
input vld_in,
input [15:0] x,
input [15:0] y,
output vld_out,
output [15:0] p
);
wire [15:0] x_out;
wire [15:0] y_out;
wire [2:0] phase_flag;
input_process u1(
.x(x),
.y(y),
.vld_in(vld_in),
.x_out(x_out),
.y_out(y_out),
.phase_flag(phase_flag)
);
cordic u2(
.clk(clk),
.rst_n(rst_n),
.x(x_out),
.y(y_out),
.phase_flag(phase_flag),
.vld_out(vld_out),
.p(p)
);
endmodule
testbench.v
module testbench ();
reg clk;
reg rst_n;
reg vld_in;
reg signed [15:0] x;
reg signed [15:0] y;
wire vld_out;
wire [15:0] p;
initial begin
vld_in <= 1'b0;
clk <= 1'b0;
rst_n <= 1'b0;
x <= 10;
y <= 10;
#10
rst_n <= 1'b1;
vld_in <= 1'b1;
#300
x <= -3;
y <= 4;
#320
x <= 3;
y <= -4;
#320
x <= -10;
y <= 0;
end
always #10 clk <= ~clk;
calc_phase u1(
.clk(clk),
.rst_n(rst_n),
.vld_in(vld_in),
.x(x),
.y(y),
.vld_out(vld_out),
.p(p)
);
endmodule
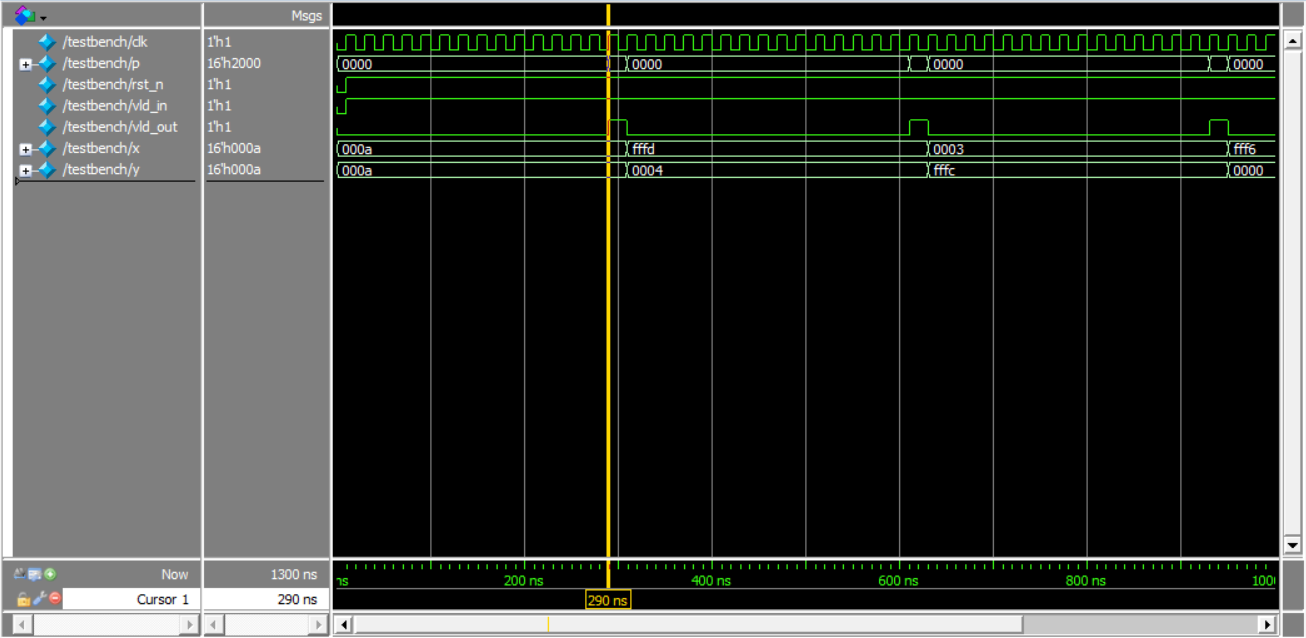
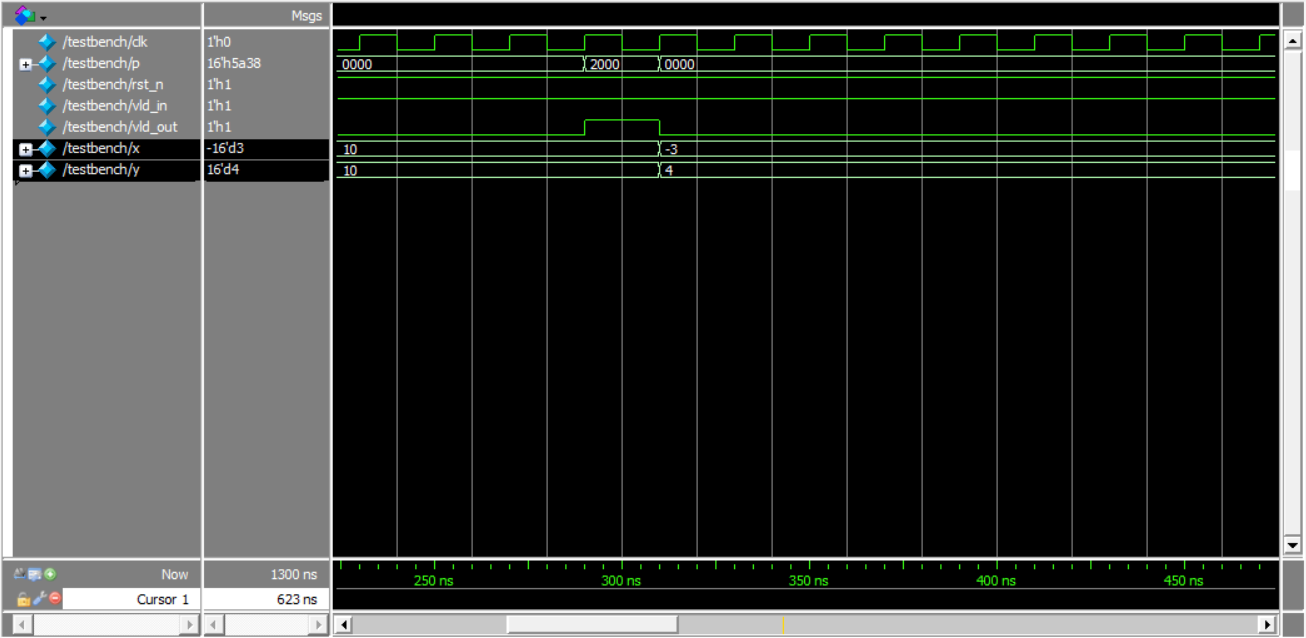
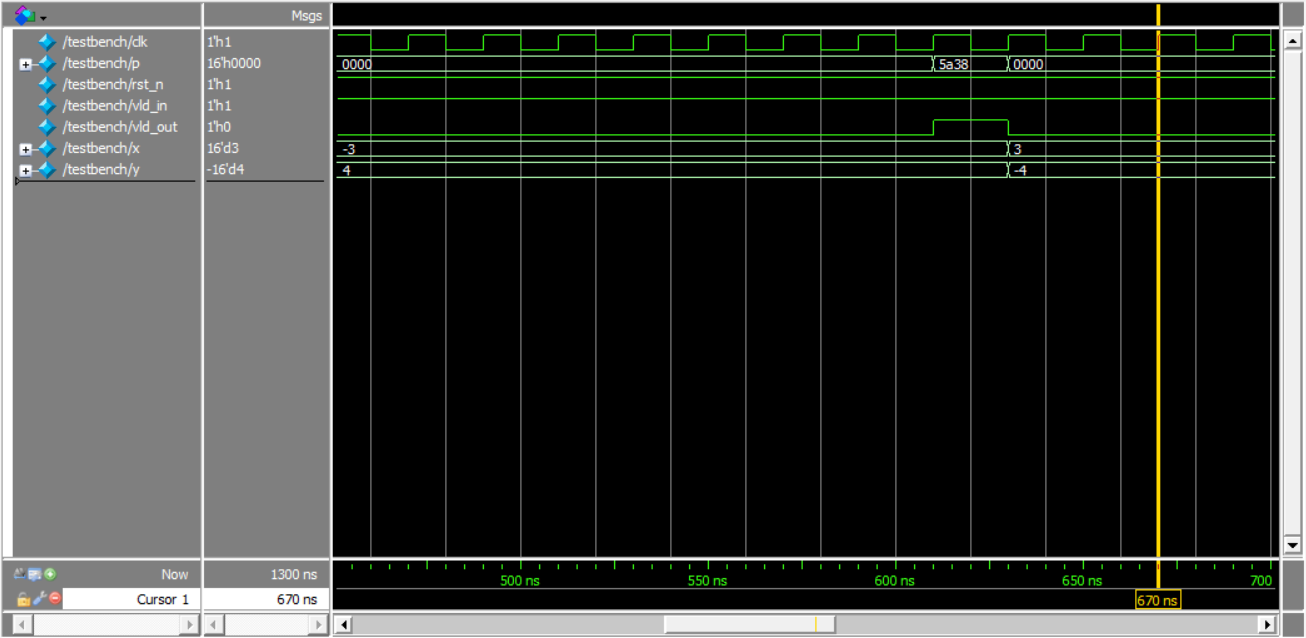
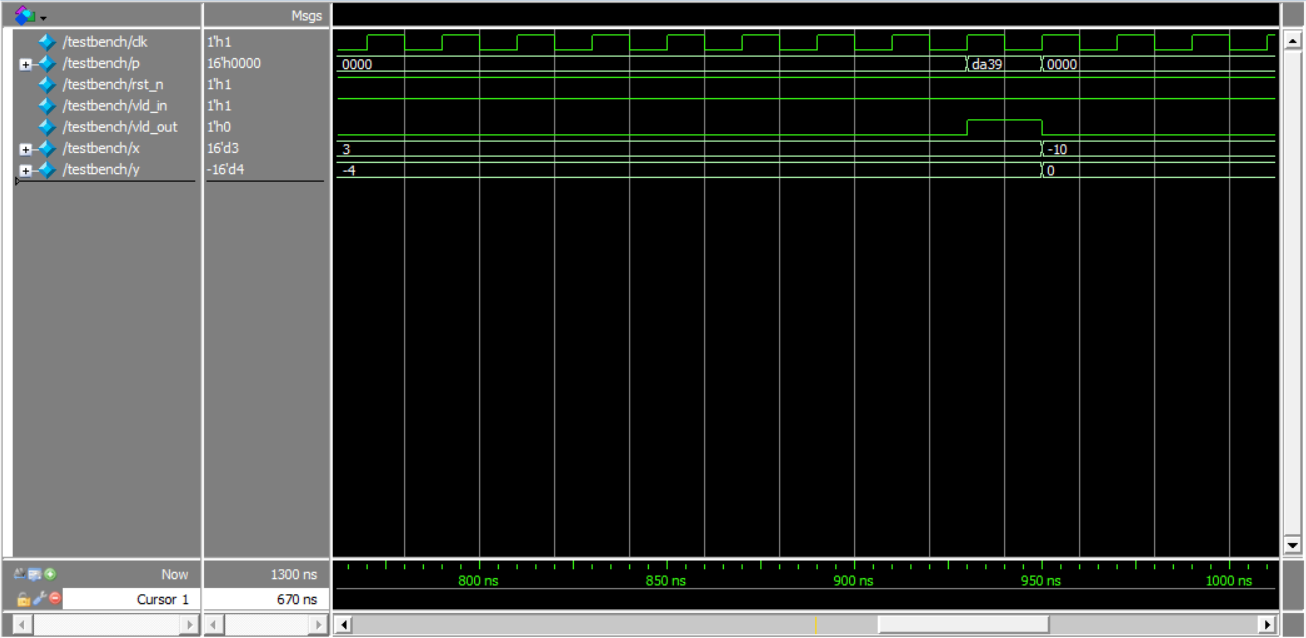
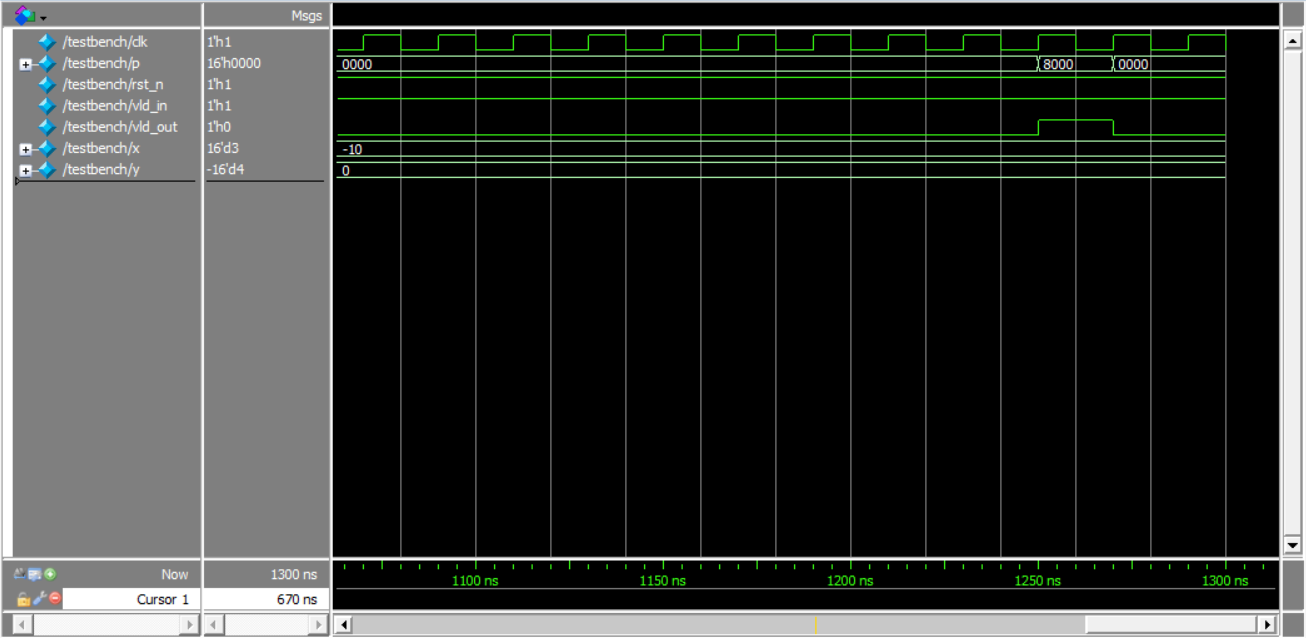
仿真结果:
数据输入15个周期后输出结果,同时产生vld_out脉冲
验证atan相位角计算结果:
X=10,Y=10 -> P = 0.25(0x2000 / 2^15)
X=-3,Y=4 -> P = 0.704834(0x5a38/ 2^15)
X=3,Y=-4 -> P = -0.295135((0xda39 – 2^16)/ 2^15)
X=-10,Y=0 -> P = -0.5 ((0x8000 – 2^16)/ 2^15)
附录:
Cordic.cpp
#include <iostream>
#include <cmath>
#include <math.h>
using namespace std;
static const double g_product_cos_table[64] = {
7.071067811865475E-1, 6.324555320336759E-1, 6.135719910778963E-1, 6.088339125177524E-1,
6.076482562561681E-1, 6.073517701412958E-1, 6.072776440935258E-1, 6.072591122988925E-1,
6.07254479332562E-1, 6.072533210898748E-1, 6.072530315291339E-1, 6.072529591389442E-1,
6.072529410413965E-1, 6.072529365170094E-1, 6.072529353859126E-1, 6.072529351031383E-1,
6.072529350324446E-1, 6.072529350147711E-1, 6.072529350103526E-1, 6.072529350092478E-1,
6.072529350089715E-1, 6.072529350089023E-1, 6.072529350088848E-1, 6.072529350088803E-1,
6.072529350088791E-1, 6.072529350088786E-1, 6.072529350088783E-1, 6.072529350088781E-1,
6.072529350088778E-1, 6.072529350088776E-1, 6.072529350088773E-1, 6.072529350088771E-1,
6.072529350088768E-1, 6.072529350088765E-1, 6.072529350088762E-1, 6.072529350088759E-1,
6.072529350088756E-1, 6.072529350088753E-1, 6.07252935008875E-1, 6.072529350088746E-1,
6.072529350088743E-1, 6.07252935008874E-1, 6.072529350088736E-1, 6.072529350088733E-1,
6.072529350088729E-1, 6.072529350088725E-1, 6.072529350088721E-1, 6.072529350088717E-1,
6.072529350088713E-1, 6.072529350088709E-1, 6.072529350088705E-1, 6.0725293500887E-1,
6.072529350088696E-1, 6.072529350088692E-1, 6.072529350088687E-1, 6.072529350088683E-1,
6.072529350088678E-1, 6.072529350088673E-1, 6.072529350088668E-1, 6.072529350088663E-1,
6.072529350088658E-1, 6.072529350088653E-1, 6.072529350088648E-1, 6.072529350088642E-1
};
/* g_atan_table[i] = atan(2^-i). when i >= 25 abs((atan(2^-i)-2^-i)/atan(2^-i)) < 1E-15. */
static const double g_atan_table[64] = {
7.853981633974483E-1, 4.636476090008061E-1, 2.449786631268642E-1, 1.243549945467614E-1,
6.241880999595735E-2, 3.123983343026828E-2, 1.562372862047683E-2, 7.812341060101111E-3,
3.906230131966972E-3, 1.953122516478819E-3, 9.765621895593194E-4, 4.882812111948983E-4,
2.441406201493618E-4, 1.220703118936702E-4, 6.103515617420878E-5, 3.05175781155261E-5,
1.525878906131576E-5, 7.62939453110197E-6, 3.814697265606496E-6, 1.907348632810187E-6,
9.536743164059609E-7, 4.768371582030889E-7, 2.38418579101558E-7, 1.192092895507807E-7,
5.960464477539055E-8, 2.98023223876953E-8, 1.490116119384766E-8, 7.450580596923828E-9,
3.725290298461914E-9, 1.862645149230957E-9, 9.313225746154785E-10, 4.656612873077393E-10,
2.328306436538696E-10, 1.164153218269348E-10, 5.820766091346741E-11, 2.91038304567337E-11,
1.455191522836685E-11, 7.275957614183426E-12, 3.637978807091713E-12, 1.818989403545856E-12,
9.094947017729282E-13, 4.547473508864641E-13, 2.273736754432321E-13, 1.13686837721616E-13,
5.684341886080801E-14, 2.842170943040401E-14, 1.4210854715202E-14, 7.105427357601002E-15,
3.552713678800501E-15, 1.77635683940025E-15, 8.881784197001252E-16, 4.440892098500626E-16,
2.220446049250313E-16, 1.110223024625157E-16, 5.551115123125783E-17, 2.775557561562891E-17,
1.387778780781446E-17, 6.938893903907228E-18, 3.469446951953614E-18, 1.734723475976807E-18,
8.673617379884035E-19, 4.336808689942018E-19, 2.168404344971009E-19, 1.084202172485504E-19
};
double my_atan2(double y, double x) {
const int n = 18;
double xt;
double z = 0.0;
double k = 1.0;
int i;
for (i = 0; i < n; i++) {
xt = x;
if (y > 0.0) {
x = x + y * k;
y = y - xt * k;
z = z + g_atan_table[i];
} else {
x = x - y * k;
y = y + xt * k;
z = z - g_atan_table[i];
}
k *= 0.5;
cout << "第" << i << "次旋转" << endl;
cout << "x = " << x << endl;
cout << "y = " << y << endl;
cout << "angle = " << z << endl;
}
return z;
}
int main(void) {
double x, y;
int phase_flag;
cin >> x >> y ;
if (x > 0 && y > 0) {
x = x;
y = y;
phase_flag = 0;
} else if (x < 0 && y > 0) {
x = -x;
y = y;
phase_flag = 1;
} else if (x < 0 && y < 0) {
x = -x;
y = -y;
phase_flag = 2;
} else if (x > 0 && y < 0) {
x = x;
y = -y;
phase_flag = 3;
} else if (x > 0 && y == 0) {
x = x;
y = y;
phase_flag = 4;
} else if (x == 0 && y > 0) {
x = x;
y = y;
phase_flag = 5;
} else if (x < 0 && y == 0) {
x = x;
y = y;
phase_flag = 6;
} else if (x == 0 && y < 0) {
x = x;
y = y;
phase_flag = 7;
}
switch (phase_flag) {
case 0:
cout << "atan = " << my_atan2(y, x) / M_PI << endl;
break;
case 1:
cout << "atan = " << 1 - ( my_atan2(y, x) / M_PI) << endl;
break;
case 2:
cout << "atan = " << -1 + (my_atan2(y, x) / M_PI) << endl;
break;
case 3:
cout << "atan = " << -1 * my_atan2(y, x) / M_PI << endl;
break;
case 4:
cout << "atan = " << 0 << endl;
break;
case 5:
cout << "atan = " << 0.5 << endl;
break;
case 6:
cout << "atan = " << -1 << endl;
break;
case 7:
cout << "atan = " << -0.5 << endl;
break;
}
}



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· 开源Multi-agent AI智能体框架aevatar.ai,欢迎大家贡献代码
· Manus重磅发布:全球首款通用AI代理技术深度解析与实战指南
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· AI技术革命,工作效率10个最佳AI工具