中国科学院大学数字集成电路作业开源——算数逻辑章节
中国科学院大学数字集成电路作业开源——第4-5章
1、基础概念问题
1.1请简要描述10进制整数与16进制整数之间相互转换方法？
方法1：将10进制整数通过除2取余数的方法得到2进制表示，再将2进制数按照每4位表示一个16进制数的方式转成16进制表示。
方法2：将10进制整数通过除16取余数的方法直接得到16进制表示。
方法1例子：30转2进制0001_1110，对应16进制1E
方法2例子：30=30/16=1余下14,14对应的是E。所以30=1E
1.2 请简要描述数的原码、反码和补码的表示方式和对应表示数值范围？
原码：原码就是符号位加上真值的绝对值, 即用第一位表示符号, 其余位表示值
[+1]原 = 0000 0001
[-1]原 = 1000 0001
8位二进制表示数的范围：[-127 , 127]
反码：正数的反码是其本身。负数的反码是在其原码的基础上, 符号位不变，其余各个位取反
[+1] = [00000001]原 = [00000001]反
[-1] = [10000001]原 = [11111110]反
8位二进制表示数的范围：[-127 , 127]
补码：正数的补码就是其本身。负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1. (即在反码的基础上+1)
[+1] = [00000001]原 = [00000001]反 = [00000001]补
[-1] = [10000001]原 = [11111110]反 = [11111111]补
8位二进制表示数的范围：[-128 , 127]
1.3 请简要描述格雷码编码方式和优点，并具体给出5位格雷码映射关系表格？
格雷码：在一组数的编码中，使得任意两个相邻的代码只有一位二进制数不同。二进制转变为格雷码通过相邻位异或实现
优点：在相邻位间转换时，只有一位产生变化。大大地减少了由一个状态到下一个状态时逻辑的混淆。
| 自然二进制数 | 5位格雷码 |
|---|---|
| 00000 | 00000 |
| 00001 | 00001 |
| 00010 | 00011 |
| 00011 | 00010 |
| 00100 | 00110 |
| 00101 | 00111 |
| 00110 | 00101 |
| 00111 | 00100 |
| 01000 | 01100 |
| 01001 | 01101 |
| 01010 | 01111 |
| 01011 | 01110 |
| 01100 | 01010 |
| 01101 | 01011 |
| 01110 | 01001 |
| 01111 | 01000 |
| 10000 | 11000 |
| 10001 | 11001 |
| 10010 | 11011 |
| 10011 | 11010 |
| 10100 | 11110 |
| 10101 | 11111 |
| 10110 | 11101 |
| 10111 | 11100 |
| 11000 | 10100 |
| 11001 | 10101 |
| 11010 | 10111 |
| 11011 | 10110 |
| 11100 | 10010 |
| 11101 | 10011 |
| 11110 | 10001 |
| 11111 | 10000 |
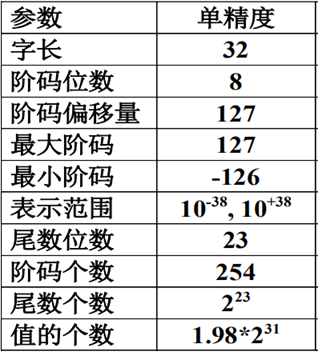
1.4 请简要描述IEEE 754标准中32位单精度浮点数格式、范围和精度？简要比较并分析浮点数和定点数在硬件实现方面的优缺点。
浮点数：优点：能够表示高精度，范围大
缺点：计算电路非常复杂
定点数：优点：计算电路很简单
缺点：不能够表示高精度，范围小
2 基于VerilogHDL进行逻辑电路设计
2.1跑表
设计一个跑表时序逻辑电路，通过按钮控制及数字显示，有时分秒显示，可以清零、开始和暂停。系统主时钟频率为10 MHz。
其中按钮Clear实现清零功能（任意状态按下时分秒值清零并停止计时）、按钮Start/Stop实现开始和暂停功能（若当前状态为停止则按下继续进行计时，若当前状态为计时则按下暂停计时）。
数字显示为XX : XX : XX形式，时分秒各为2位数字。对每位数字使用4位二进制编码输出表示（hr_h[3:0],hr_l[3:0] : min_h[3:0],min_l[3:0] : sec_h[3:0],sec_l[3:0]）。
顶层模块名为stop_watch，输入输出功能定义：
| 名称 | 方向 | 位宽 | 描述 |
|---|---|---|---|
| clk | I | 1 | 系统时钟，10 MHz |
| rst_n | I | 1 | 异步复位，低电平有效 |
| clear | I | 1 | 清零按钮，上升沿有效 |
| start_stop | I | 1 | 开始/暂停按钮，上升沿有效 |
| hr_h | O | 4 | 时高位输出，取值0~9 |
| hr_l | O | 4 | 时低位输出，取值0~9 |
| min_h | O | 4 | 分高位输出，取值0~9 |
| min_l | O | 4 | 分低位输出，取值0~9 |
| sec_h | O | 4 | 秒高位输出，取值0~9 |
| sec_l | O | 4 | 秒低位输出，取值0~9 |
设计要求：
Verilog实现代码可综合，给出综合以及仿真结果（说明：为加快仿真速度，代码用于仿真时可以缩短秒计数周期，如每100个时钟周期更新一次秒计数值，正常情况下每10000000个时钟周期才更新一次秒计数值）。
设计思路：
用counter子模块实现计数，counter子模块的功能包括：reset复位，clear清零，计数满后自动清零并输出full脉冲。
最低一级的sec_l用clk驱动，用sec_l得到full信号去驱动sec_h，用sec_h的full信号去驱动min_l……一直这样向上计数。
顶层stop_watch调用counter子模块连接实现计数功能。用两段式状态机实现STOP和START的状态切换功能，以及产生门控时钟信号，用来控制计数器工作或停止。
考虑到实际使用的合理性，在计数时，秒钟和分钟最大计数值只有59，小时可以最大计数到99（因为题目只说了跑表，没说是时钟，所以我就没有限制不超过24h）
代码实现：
counter子模块
module counter (
input clk,
input rst_n,
input clear,
input [3:0] thresh,
output full,
output [3:0] cnt_v
);
reg [3:0] cnt;
reg f;
always @(posedge clk or posedge clear or negedge rst_n) begin
if(rst_n == 1'b0) begin
cnt <= 4'b0;
f <= 1'b0;
end
else begin
if(clear == 1'b1) begin
cnt <= 4'b0;
f <= 1'b0;
end
else if(cnt_v == thresh) begin
cnt <= 4'b0;
f <= 1'b1;
end
else begin
cnt <= cnt + 1'b1;
f <= 1'b0;
end
end
end
assign cnt_v = cnt;
assign full = f;
endmodule
counter的testbench
module testbench();
reg clk;
reg rst_n;
reg [3:0] thresh;
wire full;
wire [3:0] cnt_v;
initial begin
clk <= 1'b0;
rst_n <= 1'b0;
thresh <= 4'b0000;
#10
rst_n <= 1'b1;
thresh <= 4'b1001;
end
always #10 clk <= ~clk;
counter u_cnt(.clk(clk),.rst_n(rst_n),.thresh(thresh),.full(full),.cnt_v(cnt_v));
endmodule
stop_watch顶层
module stop_watch (
input clk,
input rst_n,
input clear,
input start_stop,
output [3:0] hr_h,
output [3:0] hr_l,
output [3:0] min_h,
output [3:0] min_l,
output [3:0] sec_h,
output [3:0] sec_l
);
reg clk_en;
wire clk_gated;
parameter thresh_h = 4'b0101;
parameter thresh_l = 4'b1001;
wire full_sec_l;
wire full_sec_h;
wire full_min_l;
wire full_min_h;
wire full_hr_l;
parameter START = 1'b0;
parameter STOP = 1'b1;
reg current_state;
reg next_state;
always @(posedge clk or negedge rst_n) begin
if(rst_n == 1'b0) begin
current_state <= START;
end
else begin
current_state <= next_state;
end
end
always @(*) begin
case(current_state)
START: begin
if (clear|start_stop) begin
next_state = STOP;
clk_en = 1'b0;
end
end
STOP: begin
if (start_stop) begin
next_state = START;
clk_en = 1'b1;
end
end
default: next_state = START;
endcase
end
assign clk_gated = clk_en & clk;
counter u_cnt_0(.clk(clk_gated),.rst_n(rst_n),.clear(clear),.thresh(thresh_l),.full(full_sec_l),.cnt_v(sec_l));
counter u_cnt_1(.clk(full_sec_l),.rst_n(rst_n),.clear(clear),.thresh(thresh_h),.full(full_sec_h),.cnt_v(sec_h));
counter u_cnt_2(.clk(full_sec_h),.rst_n(rst_n),.clear(clear),.thresh(thresh_l),.full(full_min_l),.cnt_v(min_l));
counter u_cnt_3(.clk(full_min_l),.rst_n(rst_n),.clear(clear),.thresh(thresh_h),.full(full_min_h),.cnt_v(min_h));
counter u_cnt_4(.clk(full_min_h),.rst_n(rst_n),.clear(clear),.thresh(thresh_h),.full(full_hr_l),.cnt_v(hr_l));
counter u_cnt_5(.clk(full_hr_l),.rst_n(rst_n),.clear(clear),.thresh(thresh_h),.full(),.cnt_v(hr_h));
endmodule
stop_watch的testbench
module testbench();
reg clk;
reg rst_n;
reg clear;
reg start_stop;
wire [3:0] hr_l,hr_h,min_h,min_l,sec_h,sec_l;
initial begin
clk <= 1'b0;
rst_n <= 1'b0;
clear <= 1'b0;
start_stop <= 1'b0;
#1
rst_n <= 1'b1;
#10
clear <= 1'b1;
#1
clear <= 1'b0;
#10
start_stop <= 1'b1;
#1
start_stop <= 1'b0;
#10
start_stop <= 1'b1;
#1
start_stop <= 1'b0;
#10
start_stop <= 1'b1;
#1
start_stop <= 1'b0;
end
always #1 clk <= ~clk;
stop_watch u_stop_watch(
.clk(clk),
.rst_n(rst_n),
.clear(clear),
.start_stop(start_stop),
.hr_h(hr_h),
.hr_l(hr_l),
.min_h(min_h),
.min_l(min_l),
.sec_h(sec_h),
.sec_l(sec_l)
);
endmodule
仿真结果：
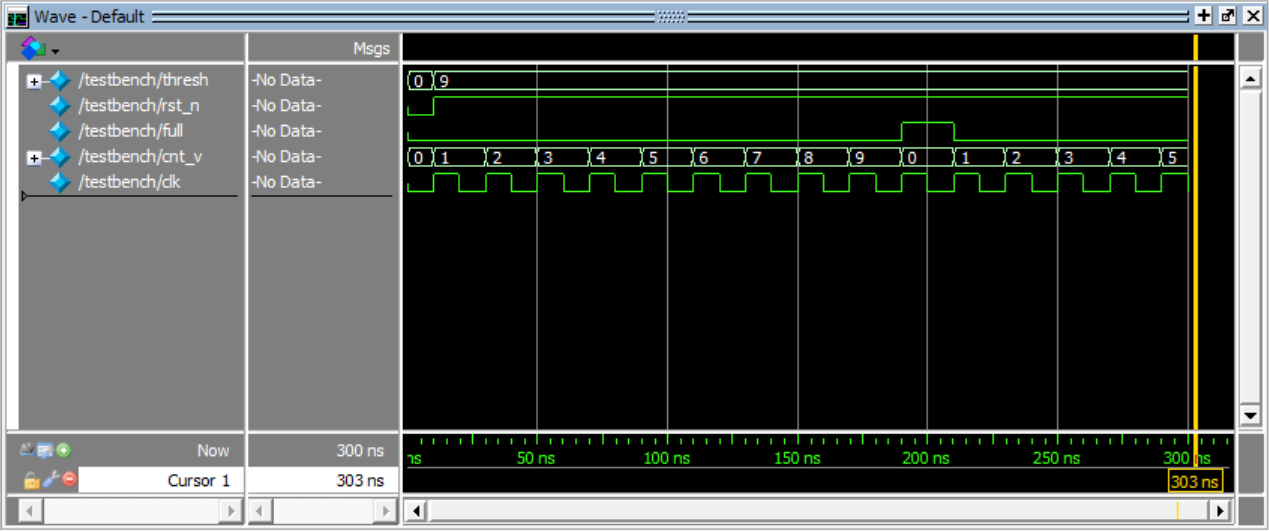
counter：计数功能，计数满后自动清零并产生full脉冲
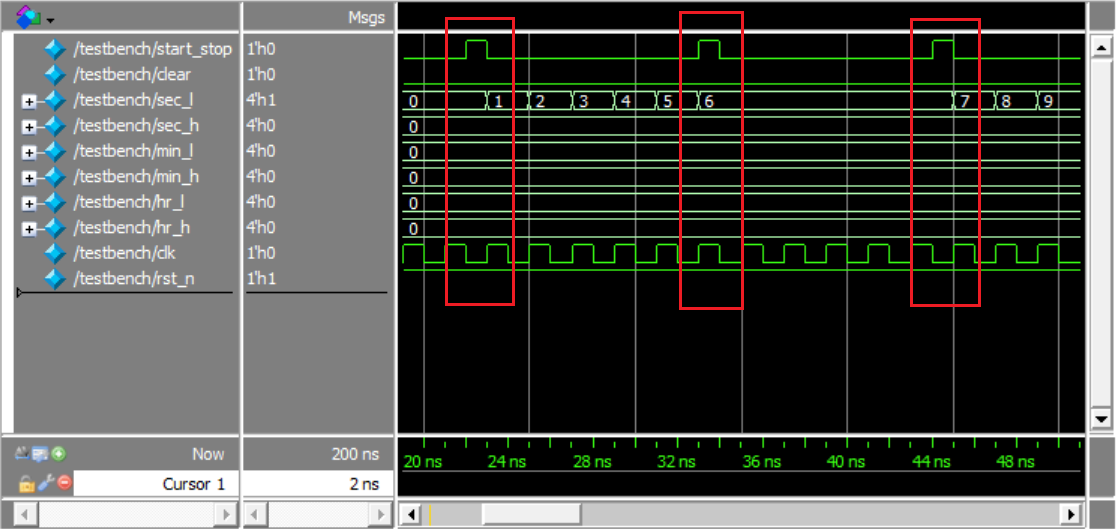
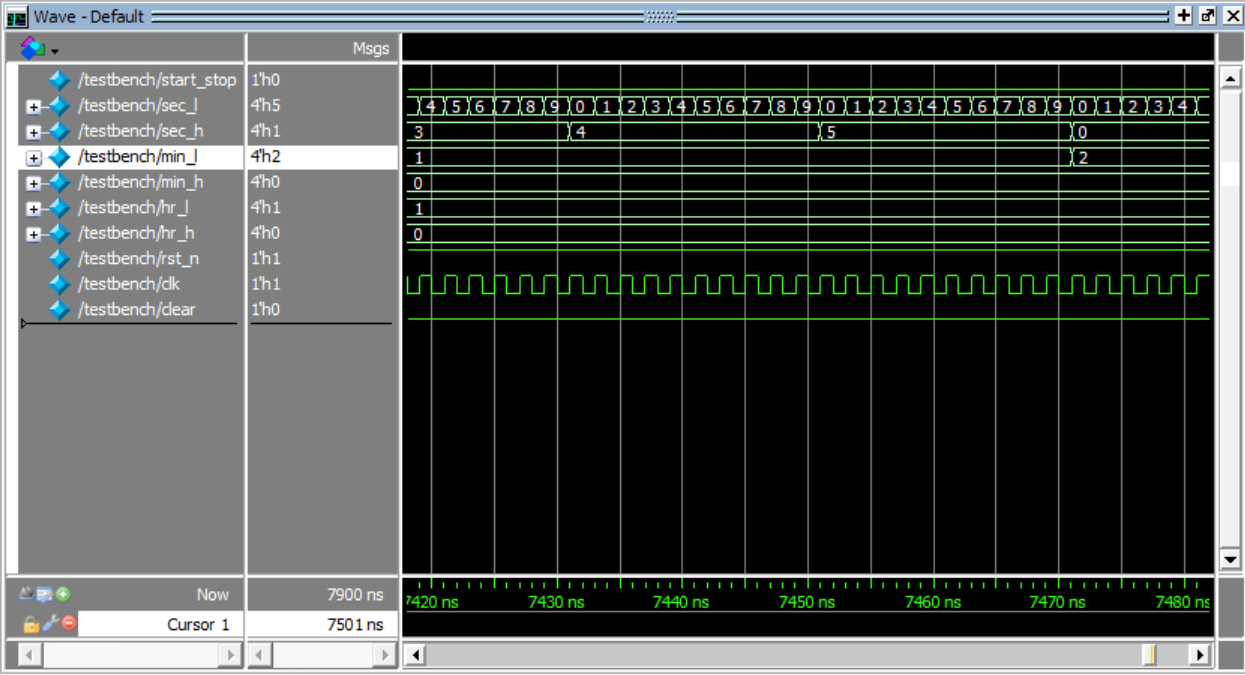
stop_watch：clear实现清零功能（任意状态按下时分秒值清零并停止计时）。
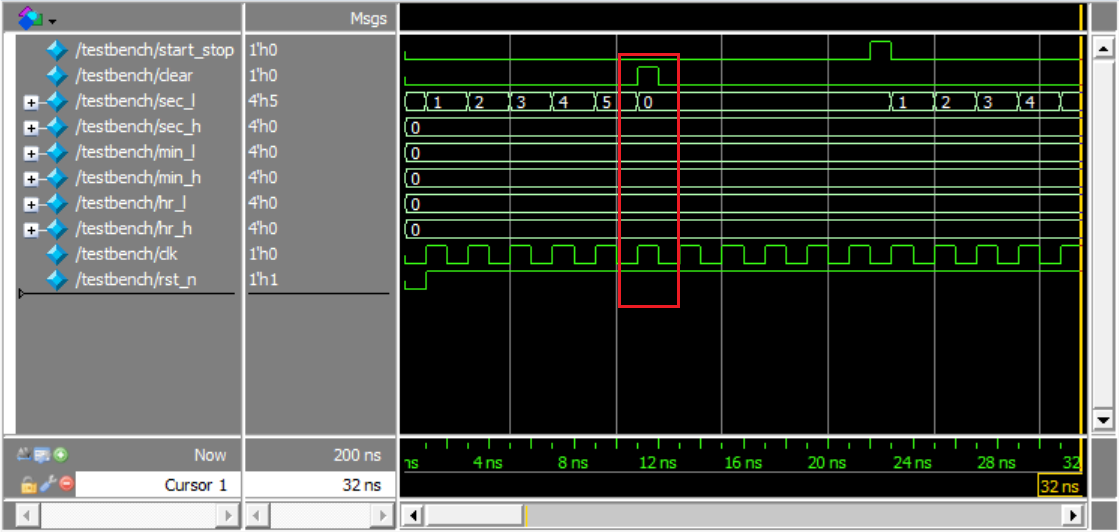
stop_watch：start/stop实现开始和暂停功能（若当前状态为停止则按下继续进行计时，若当前状态为计时则按下暂停计时）。
stop_watch：计数功能体现（00：00：00—00：02：04）
2.2快速加法器
实现快速加法器组合逻辑，要实现的功能如下：
输入为两个16位有符号数，输出17位相加结果。要求采用超前进位（Carry-look-ahead）结构。
计算例子：
0110000010000000 + 1000000000000001 = 11110000010000001
(24704) + (-32767) = (-8063)
顶层模块名为add_tc_16_16，输入输出功能定义：
| 名称 | 方向 | 位宽 | 描述 |
|---|---|---|---|
| a | I | 16 | 输入数据，二进制补码 |
| b | I | 16 | 输入数据，二进制补码 |
| sum | O | 17 | 输出和a + b，二进制补码 |
设计要求：
Verilog实现代码可综合，逻辑延迟越小越好，给出综合以及仿真结果（参考ASIC综合结果：SMIC 55nm工艺下工作时钟频率大于500 MHz）。
设计思路：
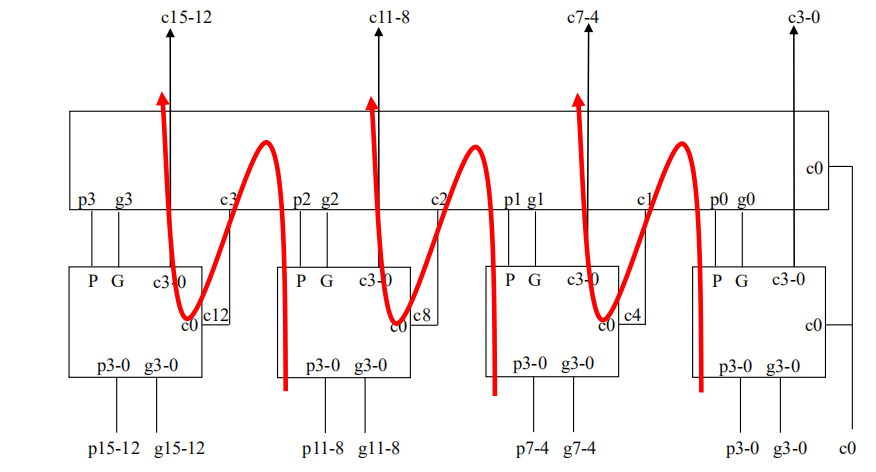
设计图纸如下图所示（红色箭头为进位传播方向）
设计子模块Carry4实现4位的进位逻辑，使用5个Carry4子模块按照图纸所示方式进行连接完成16位超前进位加法器。
对于最高位的处理，进行深入一点的思考。如果两个16位的运算没有发生溢出，那么第17位应该是符号位拓展。但如果发生了溢出的话，第17就就得作为符号位了。符号位的确定方式应该是根据最高进位来决定。所以先进行溢出检测，最高位由溢出信号来进行控制。
最后测试时我用了一组非溢出的数，和正数溢出、负数溢出各一组的数。
代码实现：
Carry4子模块
module Carry4(
input [3:0] p,
input [3:0] g,
input cin,
output P,G,
output [2:0] cout
);
assign P = &p;
assign G = g[3]|(p[3]&g[2])|(p[3]&p[2]&g[1])|(p[3]&p[2]&p[1]&g[0]);
assign cout[0] = g[0]|(p[0]&cin);
assign cout[1] = g[1]|(p[1]&g[0])|(p[1]&p[0]&cin);
assign cout[2] = g[2]|(p[2]&g[1])|(p[2]&p[1]&g[0])|(p[2]&p[1]&p[0]&cin);
endmodule
add_tc_16_16顶层
module add_tc_16_16 (
input [15:0] a,
input [15:0] b,
output [16:0] sum
);
wire [15:0] p = a|b;
wire [15:0] g = a&b;
wire [3:0] P,G;
wire [15:0] c;
wire [15:0] out;
wire overflow;
wire sign;
assign c[0] = 1'b0;
Carry4 U_Carry4_0(.p(p[3:0]),.g(g[3:0]),.cin(c[0]),.P(P[0]),.G(G[0]),.cout(c[3:1]));
Carry4 U_Carry4_1(.p(p[7:4]),.g(g[7:4]),.cin(c[4]),.P(P[1]),.G(G[1]),.cout(c[7:5]));
Carry4 U_Carry4_2(.p(p[11:8]),.g(g[11:8]),.cin(c[8]),.P(P[2]),.G(G[2]),.cout(c[11:9]));
Carry4 U_Carry4_3(.p(p[15:12]),.g(g[15:12]),.cin(c[12]),.P(P[3]),.G(G[3]),.cout(c[15:13]));
Carry4 U_Carry4_4(.p(P),.g(G),.cin(c[0]),.P(),.G(),.cout({c[12],c[8],c[4]}));
assign cout = (a[15] & b[15]) | (a[15] & c[15]) | (b[15] & c[15]);
assign out = (~a & ~b & c) | (~a & b & ~c) | (a & ~b & ~c) | (a & b & c);
assign overflow = (out[15] & ~a[15] & ~b[15]) | (~out[15] & a[15] & b[15]);
assign sign = (overflow & cout) | (~overflow & out[15]);
assign sum = {sign,out};
endmodule
testbench：
module testbench();
reg [15:0] a;
reg [15:0] b;
wire [16:0] sum;
initial begin
a <= 16'b0110_0000_1000_0000;
b <= 16'b1000_0000_0000_0001;
#10
a <= 16'b1000_0000_0000_0001;
b <= 16'b1000_0000_0000_0001;
#10
a <= 16'b0111_1111_1111_1111;
b <= 16'b0111_1111_1111_1111;
end
add_tc_16_16 U_Add16(
.a(a),
.b(b),
.sum(sum)
);
endmodule
仿真结果：
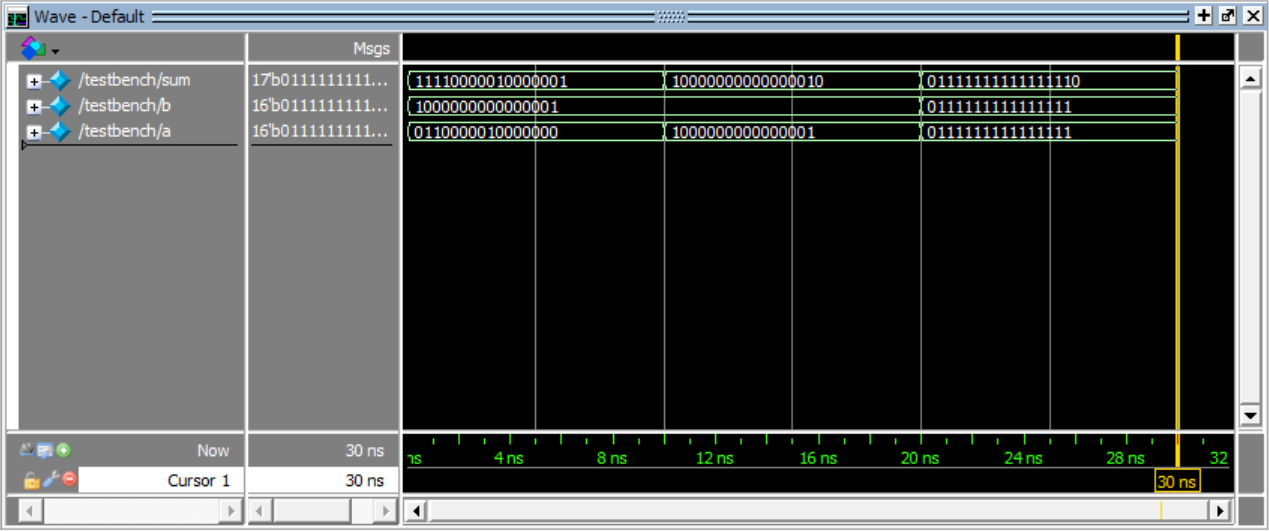
三组测试输入
0110000010000000 + 1000000000000001 = 11110000010000001
1000000000000001 + 1000000000000001 = 10000000000000010
0111111111111111 + 0111111111111111 = 01111111111111110
第一组数没有溢出，最高位是符号位拓展，后两者发生了溢出，最高位根据进位来决定
2.3快速乘法器
实现快速乘法器组合逻辑，要实现的功能如下：
输入为两个16位有符号数，输出32位相乘结果。要求采用Booth编码和Wallace树型结构。
计算例子：
0110000010000000 * 1000000000000001 = 11001111110000000110000010000000
(24704) * (-32767) = (-809475968)
顶层模块名为mul_tc_16_16，输入输出功能定义：
| 名称 | 方向 | 位宽 | 描述 |
|---|---|---|---|
| a | I | 16 | 输入数据，二进制补码 |
| b | I | 16 | 输入数据，二进制补码 |
| product | O | 32 | 输出乘积a * b，二进制补码 |
设计要求：
Verilog实现代码可综合，逻辑延迟越小越好，给出综合以及仿真结果（参考ASIC综合结果：SMIC 55nm工艺下工作时钟频率大于500 MHz）。
设计思路：
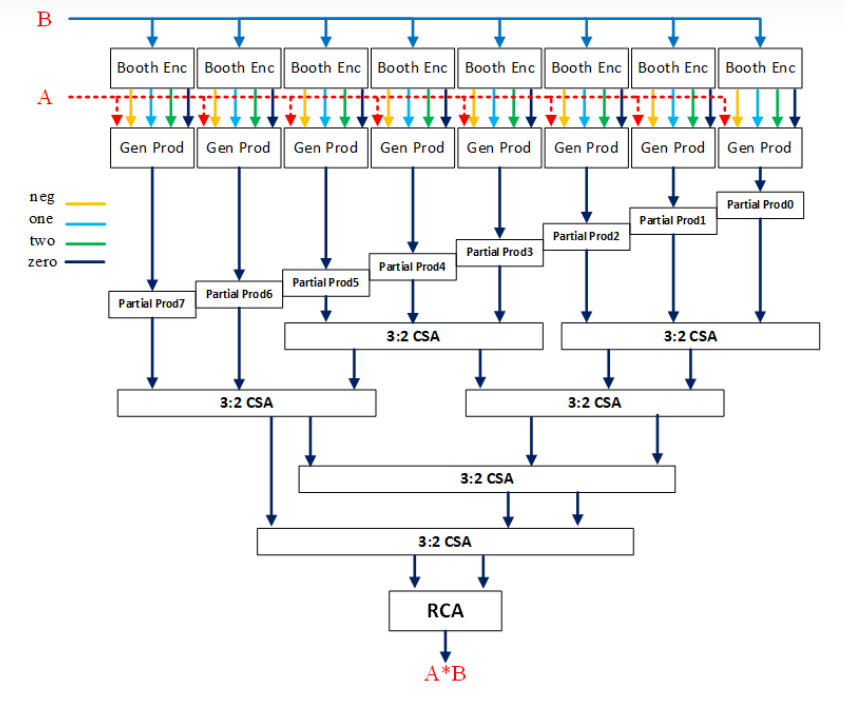
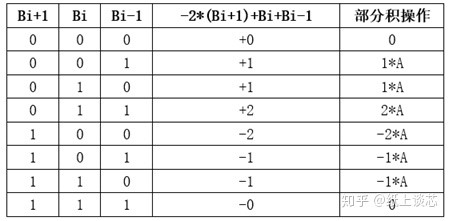
本题目要求实现16位快速乘法器，我采用了Radix-4的booth编码用于产生部分积以及wallence tree的加法器结构
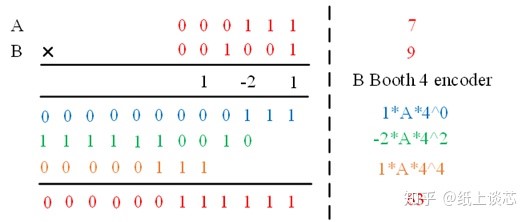
设计参考自下图：
先通过Radix-4 Booth编码电路将输入B进行编码（booth_enc），再与A一起产生8个部分积(gen_prod)，在booth子模块中进行它们的连接。这8个部分积通过Wallence Tree结构的加法树移位求和后（6个CSA (adder)），最后通过RSA（adder）求和得到乘算结果，在wallence tree子模块中进行他们的连接。顶层文件mul_tc_16_16连接booth和wallence_tree。
参考资料：https://zhuanlan.zhihu.com/p/143802580
代码实现：
booth_enc booth编码
module booth_enc (
input [2:0] code,
output neg,
output zero,
output one,
output two
);
assign neg = code[2];
assign zero = (code == 3'b000) || (code == 3'b111);
assign two = (code == 3'b100) || (code == 3'b011);
assign one = !zero & !two;
endmodule
gen_prod 用于控制部分积的产生
module gen_prod (
input [15:0] a,
input neg,
input zero,
input one,
input two,
output [31:0] prod
);
reg [31:0] prod_pre;
always @(*) begin
prod_pre = 32'b0;
if(zero) prod_pre = 32'b0;
else if(one) prod_pre = {{16{a[15]}},a};
else if(two) prod_pre = {{15{a[15]}},a,1'b0};
end
assign prod = neg ? (~prod_pre + 1'b1) : prod_pre;
endmodule
booth 完整booth编码模块
module booth (
input [15:0] a,
input [15:0] b,
output [31:0] prod_0,
output [31:0] prod_1,
output [31:0] prod_2,
output [31:0] prod_3,
output [31:0] prod_4,
output [31:0] prod_5,
output [31:0] prod_6,
output [31:0] prod_7
);
wire [7:0] neg;
wire [7:0] zero;
wire [7:0] one;
wire [7:0] two;
booth_enc u_booth_enc_0(.code({b[1:0],1'b0}),.neg(neg[0]),.zero(zero[0]),.one(one[0]),.two(two[0]));
booth_enc u_booth_enc_1(.code(b[3:1]),.neg(neg[1]),.zero(zero[1]),.one(one[1]),.two(two[1]));
booth_enc u_booth_enc_2(.code(b[5:3]),.neg(neg[2]),.zero(zero[2]),.one(one[2]),.two(two[2]));
booth_enc u_booth_enc_3(.code(b[7:5]),.neg(neg[3]),.zero(zero[3]),.one(one[3]),.two(two[3]));
booth_enc u_booth_enc_4(.code(b[9:7]),.neg(neg[4]),.zero(zero[4]),.one(one[4]),.two(two[4]));
booth_enc u_booth_enc_5(.code(b[11:9]),.neg(neg[5]),.zero(zero[5]),.one(one[5]),.two(two[5]));
booth_enc u_booth_enc_6(.code(b[13:11]),.neg(neg[6]),.zero(zero[6]),.one(one[6]),.two(two[6]));
booth_enc u_booth_enc_7(.code(b[15:13]),.neg(neg[7]),.zero(zero[7]),.one(one[7]),.two(two[7]));
gen_prod gen_prod_0(.a(a),.neg(neg[0]),.zero(zero[0]),.one(one[0]),.two(two[0]),.prod(prod_0));
gen_prod gen_prod_1(.a(a),.neg(neg[1]),.zero(zero[1]),.one(one[1]),.two(two[1]),.prod(prod_1));
gen_prod gen_prod_2(.a(a),.neg(neg[2]),.zero(zero[2]),.one(one[2]),.two(two[2]),.prod(prod_2));
gen_prod gen_prod_3(.a(a),.neg(neg[3]),.zero(zero[3]),.one(one[3]),.two(two[3]),.prod(prod_3));
gen_prod gen_prod_4(.a(a),.neg(neg[4]),.zero(zero[4]),.one(one[4]),.two(two[4]),.prod(prod_4));
gen_prod gen_prod_5(.a(a),.neg(neg[5]),.zero(zero[5]),.one(one[5]),.two(two[5]),.prod(prod_5));
gen_prod gen_prod_6(.a(a),.neg(neg[6]),.zero(zero[6]),.one(one[6]),.two(two[6]),.prod(prod_6));
gen_prod gen_prod_7(.a(a),.neg(neg[7]),.zero(zero[7]),.one(one[7]),.two(two[7]),.prod(prod_7));
endmodule
adder 加法器，可以声明位宽
module adder#(parameter DATA_WIDTH = 1) (
input [DATA_WIDTH-1:0] a,
input [DATA_WIDTH-1:0] b,
input [DATA_WIDTH-1:0] cin,
output [DATA_WIDTH-1:0] cout,
output [DATA_WIDTH-1:0] s
);
generate
genvar index;
for (index = 0; index < DATA_WIDTH ; index = index + 1'b1) begin
assign {cout[index],s[index]} = a[index] + b[index] + cin[index];
end
endgenerate
endmodule
wallence_tree 用加法器连接成wallence tree
module wallence_tree (
input [31:0] prod_0,
input [31:0] prod_1,
input [31:0] prod_2,
input [31:0] prod_3,
input [31:0] prod_4,
input [31:0] prod_5,
input [31:0] prod_6,
input [31:0] prod_7,
output [31:0] product
);
wire [31:0] csa_0_c;
wire [31:0] csa_0_s;
wire [31:0] csa_1_c;
wire [31:0] csa_1_s;
wire [31:0] csa_2_c;
wire [31:0] csa_2_s;
wire [31:0] csa_3_c;
wire [31:0] csa_3_s;
wire [31:0] csa_4_c;
wire [31:0] csa_4_s;
wire [31:0] csa_5_c;
wire [31:0] csa_5_s;
adder #(.DATA_WIDTH(32)) u_csa_0(.a(prod_0),.b(prod_1<<2),.cin(prod_2<<4),.cout(csa_0_c),.s(csa_0_s));
adder #(.DATA_WIDTH(32)) u_csa_1(.a(prod_3<<6),.b(prod_4<<8),.cin(prod_5<<10),.cout(csa_1_c),.s(csa_1_s));
adder #(.DATA_WIDTH(32)) u_csa_2(.a(csa_1_c<<1),.b(prod_6<<12),.cin(prod_7<<14),.cout(csa_2_c),.s(csa_2_s));
adder #(.DATA_WIDTH(32)) u_csa_3(.a(csa_0_c<<1),.b(csa_0_s),.cin(csa_1_s),.cout(csa_3_c),.s(csa_3_s));
adder #(.DATA_WIDTH(32)) u_csa_4(.a(csa_2_s),.b(csa_3_s),.cin(csa_3_c<<1),.cout(csa_4_c),.s(csa_4_s));
adder #(.DATA_WIDTH(32)) u_csa_5(.a(csa_2_c<<1),.b(csa_4_s),.cin(csa_4_c<<1),.cout(csa_5_c),.s(csa_5_s));
adder #(.DATA_WIDTH(32)) u_rsa(.a(csa_5_s),.b(csa_5_c << 1),.cin(32'b0),.cout(),.s(product));
endmodule
mul_tc_16_16 顶层模块
module mul_tc_16_16 (
input [15:0] a,
input [15:0] b,
output [31:0] product
);
wire [31:0] prod_0;
wire [31:0] prod_1;
wire [31:0] prod_2;
wire [31:0] prod_3;
wire [31:0] prod_4;
wire [31:0] prod_5;
wire [31:0] prod_6;
wire [31:0] prod_7;
booth u_booth(
.a(a),
.b(b),
.prod_0(prod_0),
.prod_1(prod_1),
.prod_2(prod_2),
.prod_3(prod_3),
.prod_4(prod_4),
.prod_5(prod_5),
.prod_6(prod_6),
.prod_7(prod_7)
);
wallence_tree u_wallence_tree(
.prod_0(prod_0),
.prod_1(prod_1),
.prod_2(prod_2),
.prod_3(prod_3),
.prod_4(prod_4),
.prod_5(prod_5),
.prod_6(prod_6),
.prod_7(prod_7),
.product(product)
);
endmodule
testbench
module testbench ();
reg [15:0] a;
reg [15:0] b;
wire [31:0] product;
initial begin
a <= 16'b0110_0000_1000_0000;
b <= 16'b1000_0000_0000_0001;
end
mul_tc_16_16 u_uml_tc_16_16(
.a(a),
.b(b),
.product(product)
);
endmodule
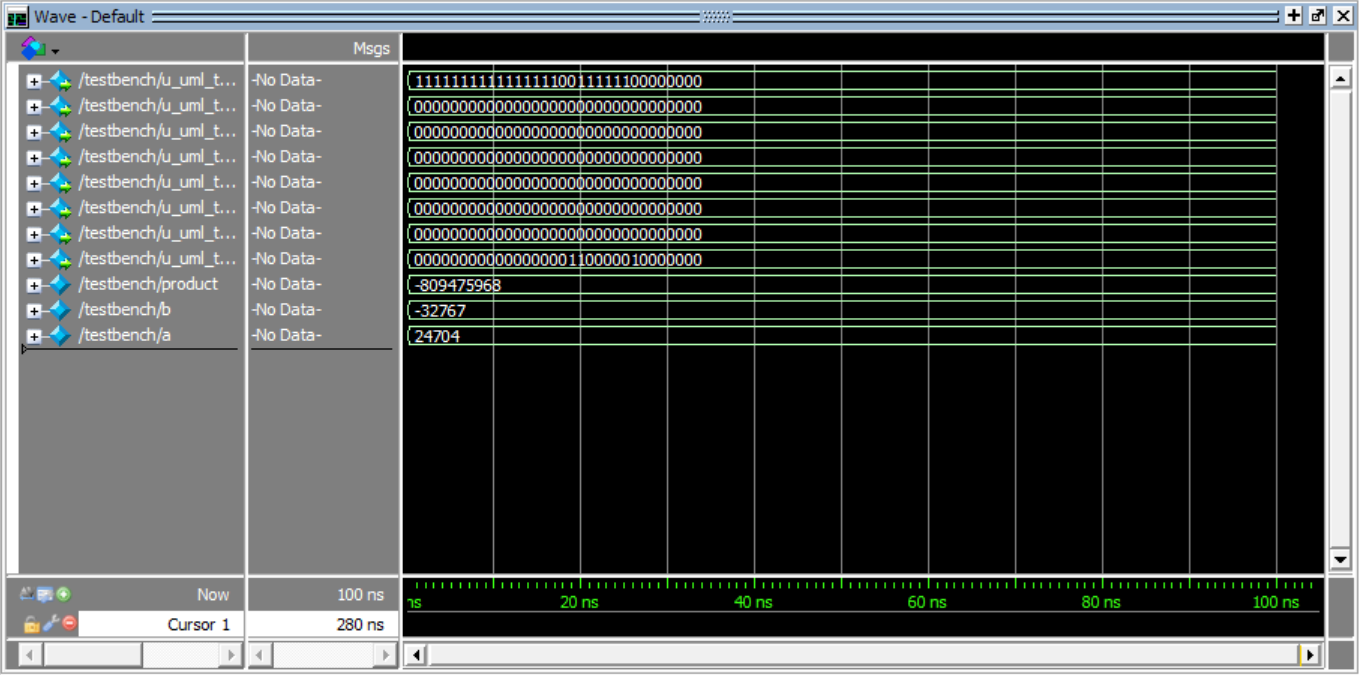
仿真结果：
0110000010000000 * 1000000000000001 = 11001111110000000110000010000000
(24704) * (-32767) = (-809475968)
部分积（prod0—prod7）与手算的结果也是一致的
2.4桶形移位器
实现桶形移位器组合逻辑，要实现的功能如下：
输入为32位二进制向量，根据方向和位移值输出循环移位后的32位结果。例如：
输入向量00011000101000000000000000000000，方向左，位移值10，输出向量10000000000000000000000001100010；
输入向量00000000111111110000000000000011，方向右，位移植20，输出向量11110000000000000011000000001111.
顶层模块名为bsh_32，输入输出功能定义：
| 名称 | 方向 | 位宽 | 描述 |
|---|---|---|---|
| data_in | I | 32 | 输入数据 |
| dir | I | 1 | 位移方向 0：循环左移 1：循环右移 |
| sh | I | 5 | 位移值，取值0~31 |
| data_out | O | 32 | 输出数据 |
设计要求：
Verilog实现代码可综合，逻辑延迟越小越好，给出综合以及仿真结果。
设计思路：
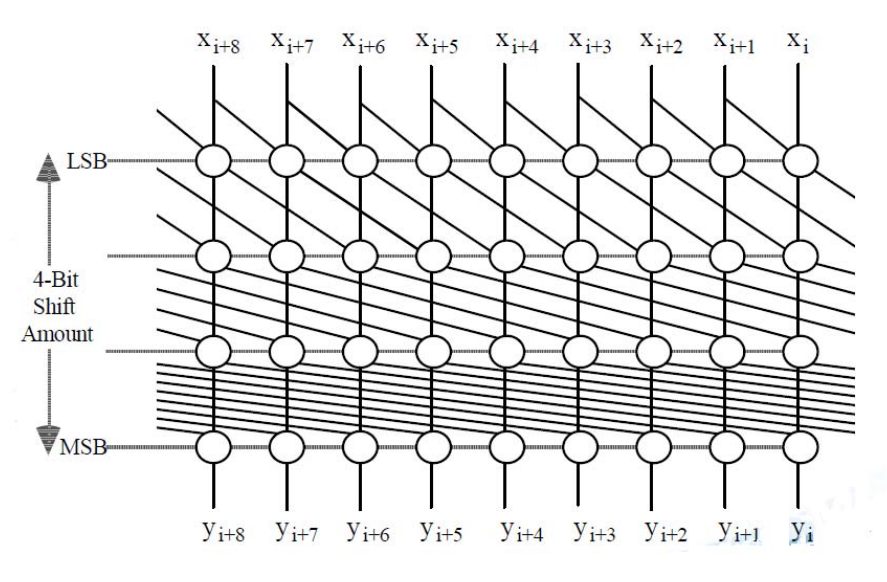
设计参考自下图：
在上图的基础上增加的功能主要有：移动方向的控制；移位码共有五位，因此共有五层的移位逻辑；循环移位。
代码实现：
module bsh_32 (
input [31:0] data_in,
input dir,
input [4:0] sh,
output [31:0] data_out
);
reg [31:0] out;
always @(*) begin
case(dir)
1'b0: begin
out = sh[0] ? {data_in[30:0], data_in[31]} : data_in;
out = sh[1] ? {out[29:0], out[31:30]} : out;
out = sh[2] ? {out[27:0], out[31:28]} : out;
out = sh[3] ? {out[23:0], out[31:24]} : out;
out = sh[4] ? {out[15:0], out[31:16]} : out;
end
1'b1:begin
out = sh[0] ? {data_in[0], data_in[31:1]} : data_in;
out = sh[1] ? {out[1:0], out[31:2]} : out;
out = sh[2] ? {out[3:0], out[31:4]} : out;
out = sh[3] ? {out[7:0], out[31:8]} : out;
out = sh[4] ? {out[15:0], out[31:16]} : out;
end
endcase
end
assign data_out = out;
endmodule
testbench
module testbench();
reg [31:0] data_in;
reg dir;
reg [4:0] sh;
wire [31:0] data_out;
initial begin
data_in <= 32'b0001_1000_1010_0000_0000_0000_0000_0000;
dir <= 1'b0;
sh <= 5'd10;
#10
data_in <= 32'b0000_0000_1111_1111_0000_0000_0000_0011;
dir <= 1'b1;
sh <= 5'd20;
end
bsh_32 u_bsh_32(
.data_in(data_in),
.dir(dir),
.sh(sh),
.data_out(data_out)
);
endmodule
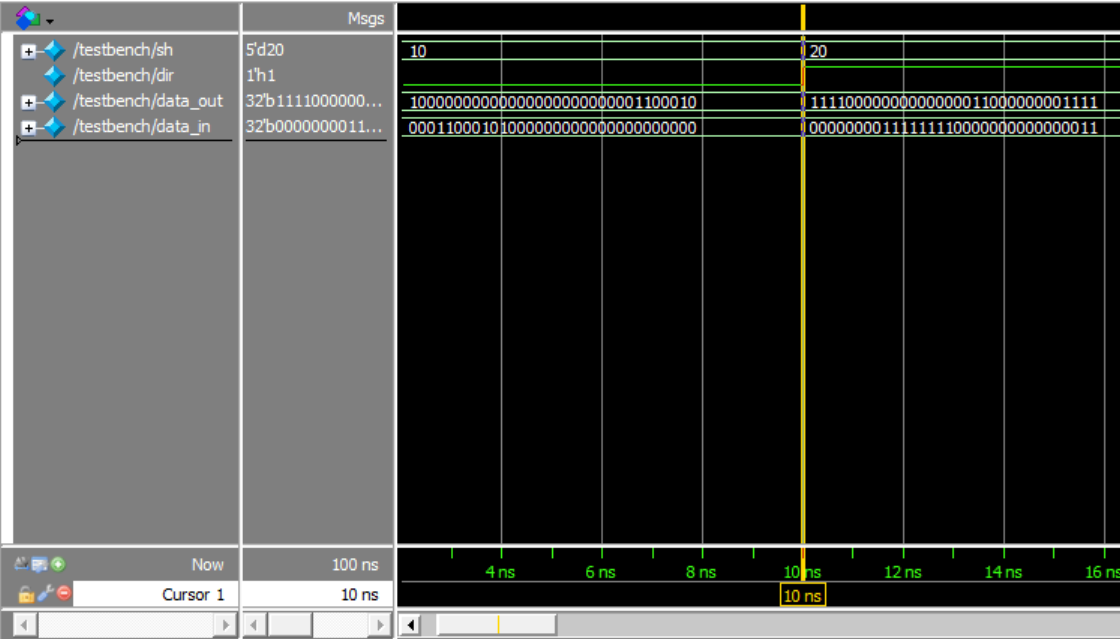
仿真结果：
输入向量00011000101000000000000000000000，方向左，位移值10，输出向量10000000000000000000000001100010；
输入向量00000000111111110000000000000011，方向右，位移值20，输出向量11110000000000000011000000001111.
