边三连通分量
https://www.luogu.com.cn/problem/P6658
洛谷仅有的题解是一个叫做 Absorb-Eject 的算法，但其实对于边三连通分量有一个更经典也更容易理解的做法（HDU6431 NewNippori）。
前置知识：
- tarjan 求边双连通分量
- 对 dfs 树的一定理解
使用 tarjan 算法求出割边之后我们考虑每个边双连通分量（不在同一个边双连通分量中的点显然也不在同一个边三连通分量中）。
首先，求出一颗 dfs 树，原图中的边可以分为树边和非树边，由于是无向图，所以树边一定只有后向边而没有前向边和横叉边。每条非树边可以看作是覆盖了一些树边，而由于是边双连通分量，所以每条树边至少被一条非树边覆盖。
如果两个点不在一个边三连通分量中，我们可以通过割掉两条边使这两点不再连通，我们考虑怎样选择要割的两条边，不难发现，有两种情况：
- 割掉一条树边和一条非树边。如果一条树边仅被一条非树边覆盖，那么我们就可以割掉这条树边以及覆盖它的非树边使图分成两部分。
- 割掉两条树边。如果覆盖两条树边的非树边集合相同，那么可以通过割掉这两条树边使图分成两部分（可以参考下图）
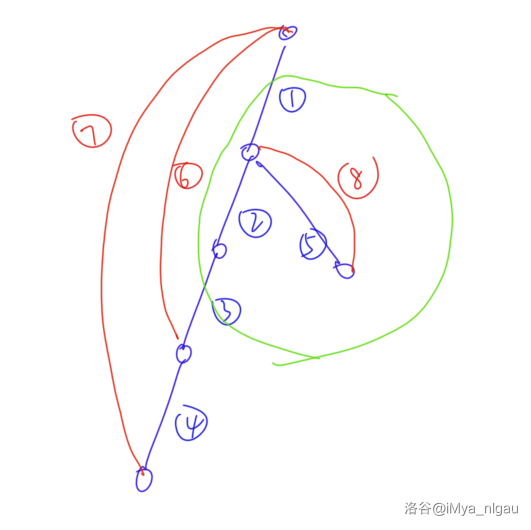
图中蓝色的边是树边，红色的边是非树边，而覆盖 \(1\) 号边和 \(3\) 号边的非树边集合相同（都是被 \(6\) 号边和 \(7\) 号边覆盖），所以割掉 \(1\) 号边和 \(3\) 号边之后图会分割成两个部分（绿色圈出的部分和其余部分）。当然，覆盖 \(2\) 号边的非树边也是 \(6\) 和 \(7\)，所以割掉 \(1\) 号边和 \(2\) 号边，或割掉 \(2\) 号边和 \(3\) 号边也能将图分成两部分。
在考虑具体怎么割之前，先讲一下如何判断覆盖一条树边的非树边。我们可以给每条非树边随机一个 \([0,2^{64})\) 内的权值。令每个点的权值为所有从该点出发的非树边的权值的异或和，这样一个点子树内所有点的权值异或和就是覆盖了这个点的父边的所有非树边的权值异或和。通过这种方式，我们就可以用 Hash 表快速判断一条树边是否只被一条非树边覆盖，两条覆盖两条树边的非树边集合是否相同。
我们把所有边的权值插入一个 Hash 表，然后对于每条树边，如果覆盖了它的非树边权值异或和在 Hash 表中，那么它仅被一条非树边覆盖，我们直接割掉这些边，图裂成很多连通块，然后对于每个连通块，我们就只需考虑情况 \(2\)。
当前的连通块里会有很多能按照情况 \(2\) 配对的树边，它们配对的方式一定是形如下图左面那种样子，即配对的树边都在一条祖孙链上，且不会出现右面两种的情况（图是自己画的，有点丑）。
图中的边都表示树边，颜色相同的边是可以配对的边。
还可能会有多条树边之间都能两两配对的情况，这是我们要选择最近的配对，这样才能让拆出的连通块中不再存在配对的树边，即三连通。
具体的，我们在 dfs 回溯的过程中维护一个 Hash 表，这样对于每条树边，我们能快速求出它下方与它配对的另一条树边，然后直接删掉两条边之间的连通块，这个连通块中一定不存在可以配对的边了，因为如果存在，也在之前的过程中删完了。这也就是说，删掉的这个连通块就是一个边三连通分量。删掉所有配对边之间部分之后，剩下的部分也是一个边三连通分量。
这样我们就以 \(O(n+m)\) 的复杂度找出了所有三连通分量。
代码（感觉还是挺短的（？）
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cctype>
#include <vector>
#include <random>
#include <ctime>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/hash_policy.hpp>
using namespace std;
using namespace __gnu_pbds;
inline int read() {
int x = 0;
char c = getchar();
while (!isdigit(c)) c = getchar();
while (isdigit(c)) x = x * 10 + (c ^ '0'), c = getchar();
return x;
}
const int maxn = 5e5 + 10;
const int maxm = 2e6 + 10;
struct Edge {
int to, next;
} edge[maxm];
int head[maxn], cnt = 1;
inline void addedge(int u, int v) { edge[++cnt] = (Edge){ v, head[u] }, head[u] = cnt; }
int n, m;
vector<vector<int> > ans;
int dfn[maxn], low[maxn], idx, cut[maxm];
void tarjan(int x, int fr) {
dfn[x] = low[x] = ++idx;
for (int i = head[x]; i; i = edge[i].next) {
if (i == (fr ^ 1))
continue;
int y = edge[i].to;
if (!dfn[y]) {
tarjan(y, i);
low[x] = min(low[x], low[y]);
if (low[y] >= dfn[y])
cut[i] = cut[i ^ 1] = true;
} else
low[x] = min(low[x], dfn[y]);
}
}
void dfs1(int, int);
void dfs2(int, int);
void dfs3(int, int, vector<int> &);
typedef unsigned long long ull;
mt19937 rnd(time(NULL));
inline ull get_rnd() { return rnd() | 1ull * rnd() << 32; }
ull w[maxn];
gp_hash_table<ull, bool> st;
gp_hash_table<ull, int> mp;
int _dfn[maxn], _idx;
bool on_tree[maxm], cut1[maxm];
int fa[maxn];
void dfs1(int x, int fr) {
_dfn[x] = ++_idx;
for (int i = head[x]; i; i = edge[i].next) {
if (i == (fr ^ 1) || cut[i])
continue;
int y = edge[i].to;
if (_dfn[y]) {
if (_dfn[y] > _dfn[x])
continue;
ull val = get_rnd();
w[x] ^= val, w[y] ^= val;
st[val] = true;
} else {
on_tree[i] = true, fa[y] = x;
dfs1(y, i);
w[x] ^= w[y];
}
}
if (st.find(w[x]) != st.end())
cut1[fr] = cut1[fr ^ 1] = true;
if (cut1[fr] || !fr) {
mp.clear();
dfs2(x, 0);
vector<int> tmp;
dfs3(x, 0, tmp);
ans.push_back(tmp);
}
}
void dfs2(int x, int fr) {
for (int i = head[x]; i; i = edge[i].next) {
int y = edge[i].to;
if (cut[i] || cut1[i] || !on_tree[i])
continue;
dfs2(y, i);
}
if (mp.find(w[x]) != mp.end()) {
int y = mp[w[x]];
vector<int> tmp;
dfs3(x, y, tmp);
ans.push_back(tmp);
on_tree[fr] = false;
addedge(fa[x], y);
on_tree[cnt] = true, fa[y] = fa[x];
mp[w[x]] = y;
} else
mp[w[x]] = x;
}
void dfs3(int x, int t, vector<int> &v) {
v.push_back(x);
for (int i = head[x]; i; i = edge[i].next) {
int y = edge[i].to;
if (cut[i] || cut1[i] || !on_tree[i] || y == t)
continue;
dfs3(y, t, v);
}
}
int main() {
n = read(), m = read();
for (int i = 1; i <= m; i++) {
int u = read(), v = read();
addedge(u, v), addedge(v, u);
}
for (int i = 1; i <= n; i++)
if (!dfn[i])
tarjan(i, 0);
for (int i = 1; i <= n; i++)
if (!_dfn[i])
dfs1(i, 0);
for (vector<int> &v : ans) sort(v.begin(), v.end());
sort(ans.begin(), ans.end());
printf("%d\n", ans.size());
for (vector<int> v : ans) {
for (int x : v) printf("%d ", x);
puts("");
}
return 0;
}
参考资料：
