算法合集
时间和空间复杂度的介绍
- 时间复杂度:
-
时间复杂度是用来估计算法运行时间的一个式子(单位)
-
一般来说,时间复杂度高的算法运行时间越慢
-
常见的时间复杂(按效率排序) :
O(1) < O(LogN) < O(N) < O(n * logN) < O(n * n) < O(n * n logN) < O(n * n * n
- 空间复杂度
-
用来评估算法内存占用大小的式子
-
空间复杂度的表达方式与时间复杂度完全一样
算法使用的几个变量:O(1) 算法使用了长度为n的一维列表:O(n) 算法使用了m行n列的二维列表:O(mn) -
通常以空间换取时间
冒泡排序
原理:
从第一个数开始,与它下一个相邻的数比较大小。比它大就交换位置,比它小不交换,就拿这个相邻数与下一个数比较。重复下去,到最后一个元素时。就得到了一个最大的值。
列表的长度是len(a),但是当只剩下最后一个数需要比较大小时,它已经是最小的了,所以一共要走len(a) - 1次
第一次需要比较的次数是len(a) - 1 得到一个最大值
第二次需要比较的次数是len(a) - 1 - 1
第三次需要比较的次数是len(a) - 1 - 1 - 1
所以每次需要比较的次数是 len(a) -i -1
优化:如果列表本身就是有序的[1,2,3,4,5,6,7,8,9],或者中途排好序了。那么还需要比较大小交换位置吗?
时间复杂度:
最坏:O(n^2)
最好:就是本身就是有序的时候,O(n)
代码实现
li = [8, 3, 4, 7, 2, 5, 6, 9, 1]
# li = [1,2,3,4,5,6,7,8]
def bubble(li):
for i in range(len(li) - 1): # 总次数
flag = False # 加标志位
for j in range(len(li) - i - 1): # 需要比较的次数
if li[j] > li[j + 1]:
li[j], li[j + 1] = li[j + 1], li[j] # 交换两个数
flag = True
print('第%d次排序:'%(i+1), li)
if not flag:
break # 某一次比较时列表里没有数需要交换。退出外层循环
bubble(li)
print(li)
选择排序
原理:取一个基准数,暂且定为第一个,拿第一个数和剩下的数中最小的数交换位置,之后再拿第二个数和它剩下的数中最下的数交换位置,依次进行下去
核心:基准数和剩下的数比较大小时,注意记录此时最小数的索引
例如:
# li = [2,4,5,1,6,9,7,3,8]
li = [3,4,5,2,6,9,7,1,8]
li = [1,4,5,2,6,9,7,3,8]
li = [1,2,5,4,6,9,7,3,8]
li = [1,2,3,4,6,9,7,5,8]
li = [1,2,3,4,5,9,7,6,8]
li = [1,2,3,4,5,6,7,9,8]
li = [1,2,3,4,5,6,7,8,9]
优化:当基准数已经是最小数的时候,不需要交换
实现
li = [2, 4, 5, 1, 6, 9, 7, 3, 8]
# li = [1,2,3,4,5,6,7,8,9]
def select_sort(li):
# 总共需要交换的次数 i代表基准数的索引
for i in range(len(li) - 1):
mid = i
# 剩下的数中比它小就交换位置,并记录那个最小的数的索引
# 优化,如果后面的数都比基准数大,说明他已经是最小的数了。不需要进行交换。
for j in range(i + 1, len(li) - 1):
if li[j] < li[mid]:
# 此时最小数的索引
mid = j
if mid != i:
li[mid], li[i] = li[i], li[mid]
print('第%d次排序' % (i + 1), li)
select_sort(li)
print(li)
插入排序
原理:
和我们平时抓牌一样。
假设手里已经有了第一张牌,之后的每一次抓牌与手里的牌的比较大小(从右往左),大就放这张牌的后面。小就把这张牌往后移动,与手里剩下的牌比较。直到大于手里的牌。
重复以上步骤,当我们的牌抓完时,手里的牌也就排好序了,所以一共要抓len(li) - 1 次
注意点:如果抓到的牌,一直比手里的牌小,j就要一直减,但是减到列表的第一个索引的数往右移动一个位置的时候就可以不用减了,直接把抓到的牌放到第一个索引即可。
时间复杂度:
最好:O(n):当抓到的牌一直比手里的大的时候,就不需要移动牌,直接放牌就行了。不走while循环
最坏:O(n^2)
实现
li = [8, 3, 4, 7, 2, 5, 6, 9, 1]
# li = [1, 2, 3, 4, 5, 6, 7, 8, 9]
def insert_sort(li):
for i in range(1, len(li)): # i 抓到的牌的索引。从一开始
tmp = li[i] # 临时存放抓到的牌的值
j = i - 1 # 手里的牌的索引。从右开始
while j >= 0 and li[j] > tmp: # 手里的牌大于抓的牌 j往右移动一位置 注意点
li[j + 1] = li[j]
j -= 1
li[j + 1] = tmp # 放牌
insert_sort(li)
print('排完序之后:', li)
快速排序
原理:
随机找一个基准数 ,暂且为第一个。把这个数拿出来。此时有个空位。然后从最右边开始找比他小的数。找到之后,把小的数放到空位上。然后从左边开始找比它大的数,放到空位上
li = [8, 3, 4, 7, 2, 5, 6, 9, 1]
li = [1, 3, 4, 7, 2, 5, 6, 9, ] 8
li = [1, 3, 4, 7, 2, 5, 6, ,9 ] 8
.
.
.
li = [1, 3, 4, 7, 2, 5, 6, 8,9 ] 8
几次之后 保证左边的数都比基准数小,右边的数都比基准数大
递归调用就可完成排序
实现
li = [8, 3, 4, 7, 2, 5, 6, 9, 1]
def partition(li, left, right):
tmp = li[left] # 临时存放基准数
while left < right:
while left < right and li[right] >= tmp: # 右边找比tmp小的数
right -= 1 # 比基准数大 向左移动一位置
li[left] = li[right] # 找到之后 把数放到左边的空位上
while left < right and li[left] <= tmp: # 左边找比tmp大的数
left += 1 # 比基准数大,向右移动一位置
li[right] = li[left] # 找到之后。把数放到右边的空位上
li[left] = tmp # 当left 和right重合时,表示左边的数都比基准数小,右边的数都比基准数大,所以把基准数放到重合的位置上
return left
def quick_sort(li, left, right):
if left < right:
mid = partition(li, left, right) # 得到基准数最后的的索引
quick_sort(li, left, mid - 1)
quick_sort(li, mid + 1, right)
quick_sort(li, 0, len(li) - 1)
print(li)
归并排序
原理:
前提是必须确保这个列表左右两边有序
例如:[2,5,7,8,9,1,3,4,6]
以9为中心
2 和 1比较 [].append(1)
2 和 3比较 [1].append(2)
3 和 5比较 [1,2].append(3)
.
.
.
最后得到新列表:[1,2,3,4,5,6,7,8,9]
去除假设:利用递归。分解,合并,归并一步完成
复杂度: O(NlogN) 当n等于16层时,他一共要执行4次func() 每一个func就是O(n) 所以就是 N * logN
实现
def merge(li, low, mid, high):
i = low
j = mid + 1
tmp = []
while i <= mid and j <= high:
if li[i] < li[j]:
tmp.append(li[i])
i += 1
else:
tmp.append(li[j])
j += 1
# while执行完毕后,肯定有一边先没数了
while i <= mid:
# 左边还有数,加到[]
tmp.append(li[i])
i += 1
while j <= high:
# 右边还有数,加到[]
tmp.append(li[j])
j += 1
li[low:high + 1] = tmp
def merge_sort(li, low, high):
# 至少有两个元素
if low < high:
mid = (low + high) // 2
merge_sort(li, low, mid)
print(low,mid,high)
merge_sort(li, mid + 1, high)
merge(li, low, mid, high)
li = [2, 5, 7, 8, 9, 1, 3, 4, 6]
merge_sort(li, 0, 8)
print(li)
什么是二分查找?
- 特点:二分查找又称折半查找。每次查找都会使数目减少一半
- 优点:比较次数少、查找速度快
- 缺点:必须是有序的
实现
def binary_search(l1, val):
"""
二分查找
:param l1: 待查列表
:param val: 待查元素
:return: 返回索引
"""
# 左边起始位置索引和右边结束位置索引
left, right = 0, len(l1) - 1
while left <= right:
mid = (left + right) // 2
if val > l1[mid]:
left = mid + 1
elif val < l1[mid]:
right = mid -1
else:
return mid
res = binary_search(l1,55)
print(res)
小青蛙跳台阶问题
一致青蛙一次可以跳上1级台阶,也可以跳上2级台阶,求该青蛙跳上一个n级的台阶有多少中跳法?
假设,一级台阶,有f(1)种方法,二级台阶有f(2)种方法,以此类推,跳到n级台阶有f(n)种方法。
可以看出,f(1) = 1,f(2) = 2。那么,n级台阶就有两种情况。
- 跳1级,接下来是f(n - 1)
- 跳2级,接下来是f(n - 2)
总数就是f(n) = f(n - 1) + f(n - 2)
def memo(func):
cache = {}
def inner(*args, **kwargs):
if args not in cache:
cache[args] = func(*args, **kwargs)
return cache[args]
return inner
@memo
def fbi(n):
if n <= 2:
return 1
return fbi(n - 1) + fbi(n - 2)
print(fbi(100))
一致青蛙一次可以跳上1级台阶,也可以跳上2级台阶,也可以一次跳n级台阶,求该青蛙跳上一个n级的台阶有多少中跳法?
def memo(func):
cache = {}
def inner(*args, **kwargs):
if args not in cache:
cache[args] = func(*args, **kwargs)
return cache[args]
return inner
@memo
def fbi(n):
if n <= 2:
return 1
return 2 * fbi(n - 1)
print(fbi(100))
二叉树
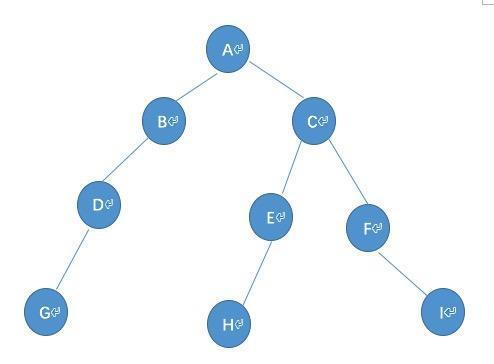
创建和遍历
# -*- coding:utf-8 -*-
class TreeNode:
def __init__(self, x, left=None, right=None):
self.val = x
self.left = left
self.right = right
@staticmethod
def before(self):
"""
前序遍历 根 左 右
:param self:
:return:
"""
if not self:
return
print(self.val)
self.before(self.left)
self.before(self.right)
@staticmethod
def middle(self):
"""
中序遍历,左 根 右
:param self:
:return:
"""
if not self:
return
self.middle(self.left)
print(self.val)
self.middle(self.right)
@staticmethod
def after(self):
"""
右序遍历 左 右 根
:param self:
:return:
"""
if not self:
return
self.after(self.left)
self.after(self.right)
print(self.val)
@staticmethod
def depth(self):
"""
层次遍历
:return:
"""
if not self:
return
res, q = [],[]
# 根节点入队
q.append(self)
# 循环 q 队列
while q:
# 取出第一个元素
node = q.pop(0)
# 把节点的值加到列表
res.append(node.val)
# 如果节点的左边有节点,入队
if node.left:
q.append(node.left)
# 如果节点的右边有节点,入队
if node.right:
q.append(node.right)
return res
def __str__(self):
return self.val
root = TreeNode(
'A',
TreeNode('B',
TreeNode('D',
TreeNode('G')),
),
TreeNode('C',
TreeNode('E',
TreeNode('H')),
TreeNode('F',
right=TreeNode('I'))
)
)
# 验证
# print(root)
# print(root.left)
# print(root.right)
# print(root.left.left)
# print(root.right.left)
# root.before(root)
# root.middle(root)
root.after(root)
print(root.depth(root))
非学,无以致疑;非问,无以广识


