打印圣诞树

打印圣诞树

今天遇到一个不算特别变态的题目，可是却往错误的方向思考了有一会儿。

这是这个题目的链接：[打印圣诞树](圣诞树_牛客题霸_牛客网 (nowcoder.com))

题目大致意思是，给定一个高度，打印出圣诞树。

效果图类似以下这种：

错误示范

首先我把每片叶子看作是5X3的矩形，空白看作是3X3的矩形。

最上面为第1层，最下面为第n层。

第i层前面有n-i个空矩形。

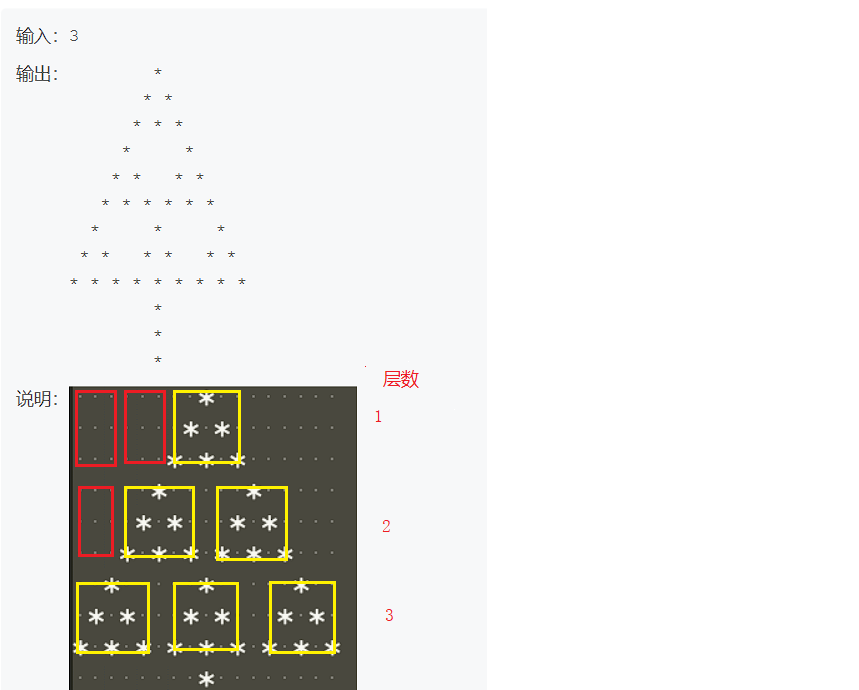
于是，我就想到了下面的代码：

#include"stdio.h"
void print_empty();//打印空矩形,只含一个printf函数
void print_53();//打印三角矩形，只含一个printf函数
int main()
{
    int n=0;
    scanf("%d",&n);//n是输入的圣诞树高度
    for(int i=1;i<n+1;i++)//到第i层
    {
        for(int j=0;j<n-i;j++)//第i层有n-i个空矩形
            print_empty();
        for(int j=0;j<i;j++)//第i层有i个53矩形
            print_53();
        printf("\n");
    }
    return 0;
}
void print_empty()
{
    printf("   \n"
           "   \n"
           "   \n");
}
void print_53()
{
    printf("  *  \n"
           " * * \n"
           "* * *\n");
}

突然我想到，在打印空矩形和53矩形时换了行，我要怎么保证两个矩形在同一行呢？

果不其然，结果成了这样。

而且，这种方式还有一个缺点，就是两个53矩形之间还有一行没考虑，自然更不可能得到正确答案。

正确姿势

代码

直接上代码，再解释：

#include <stdio.h>
void print_empty_3();//输出3个空格
void print_level(int l);//打印矩形第l行
int main()
{
    //不妨把圣诞树的每片三角形看作是 6X3 的矩形
    //把矩形看作一个元素，那么从上到下，共n层，从第一层开始看
    //第i层先有空白矩形n-i个，有三角形矩形i个

    //这样在每层的内部，还有三行，从上到下3行，从第一行开始看
    //第j行先有空白矩形行（n-i）个,之后有i个第j行矩形
    int n=0;
    scanf("%d",&n);
    for (int i = 1; i < n+1; ++i)//控制第几层
    {
        for (int j = 1; j <=3; ++j)//到了第i层的第j行，控制行
        {
            for (int k = 0; k < n-i; ++k) //第j行先有空白
            {
                print_empty_3();
            }
            for (int k = 0; k < i; ++k) //打印i个矩形第j行
            {
                print_level(j);
            }
            printf("\n");//每行输出完后换行
        }
    }
    //最后，还有一个高n行的树根
    //这个树根的位置在第nX3列
    for (int i = 0; i < n; ++i)//控制树根高度为n
    {
        for (int j = 0; j < n*3-1; ++j)
        {
            printf(" ");
        }
        printf("*\n");
    }
}
void print_empty_3()
{
    printf("   ");
}
void print_level(int l)
{
    if (1==l)
        printf("  *   ");
    else if(2==l)
        printf(" * *  ");
    else if(3==l)
        printf("* * * ");
}

解释

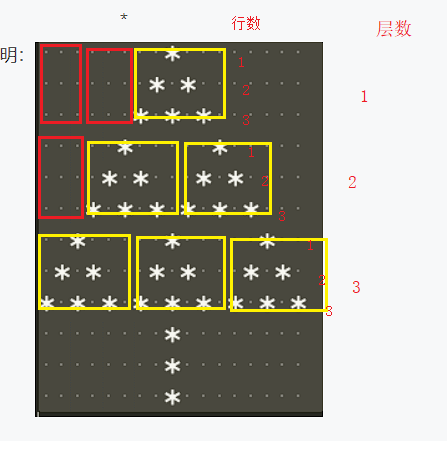
这个版本中，我将圣诞树的每片三角形看作是6X3的矩形，用以解决5X3矩形时两个矩形中间有缺口的问题

，并且把每层矩形再分为3行。

思路

树叶思路

从第一层开始从上往下共n层，第i层先有(n-i)个空矩形，i个六三矩形。

每一层从第一行开始从上往下共3行，每行先打印(n-i)个单行空矩形，也就是(n-i)*3个空格。

在打印第j行的单行矩形，这里用 void print_level(int l),函数接收第几行，就打印六三矩形的第几行，

一行打印完不忘换行 printf("\n"); 。

树根思路

至于最后的树根，这个很简单，找规律即可：

当n=1时，树根长1，在占用行的第3个字符处;

当n=2时，树根长2，在占用行的第6个字符处;

当n=3时，树根长3，在占用行的第9个字符处;

所以，树根长n，在占用行的第n*3个字符处;

所以，来一个嵌套循环即可:

外层循环控制行，内层循环控制空格字符数，到n*3的位置时停止打印空格，打印“*”。

    for (int i = 0; i < n; ++i)//控制树根高度为n
    {
        for (int j = 0; j < n*3-1; ++j)
        {
            printf(" ");
        }
        printf("*\n");
    }

最终效果