运筹学之"图解法求出最优解和最大利润"

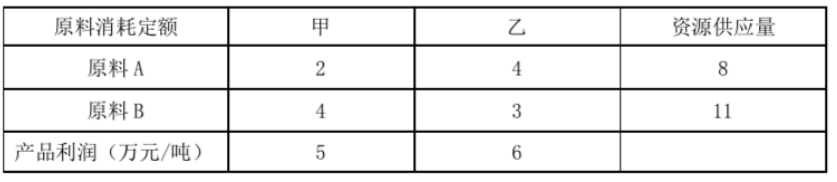
11、某公司利用两种原料 A、B 生产甲、乙两种产品（吨），各产品所需的原料数，原料限量及单位产品所获利润如下表。企业目标是追求利润的最大化，试写出该线性规划问题的数学模型，并用图解法求出最优解和最大利润。

 解题思路:

 

 

 

1. 最大总利润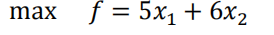也就是
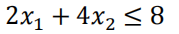2. 是一条线A和B的二元一次不等式方程,
   1. 因这里要最大的值,所以完全可以将 不等式变为等式,
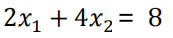   2. 地标为A(X1,X2)当求A的时候可以从图中看出X1是0,
   3. 然我们一开始没有图,可以假设为0,这样就可以求出X2的值,这样A(0,X2)的地表就出来了,
   4. B地标求法同理,假设X2=0,这样就是可以求出X1的值,后B(X1,0)的地标就出来了,
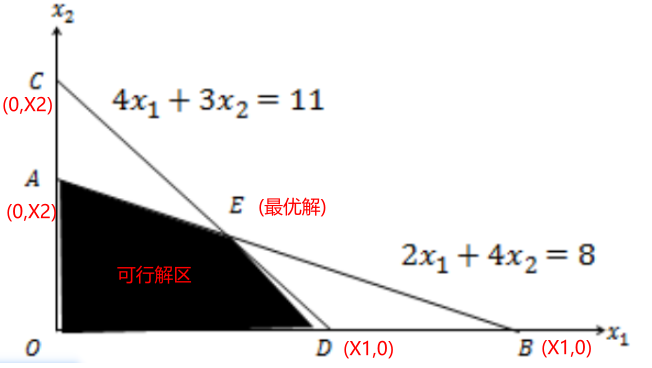
   5. 根据这两个点就可以画出可行区域的A点到B点的线

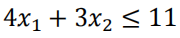3.  是另一条线C和D的二元一次不等式方程

1. 因这里要最大的值,所以完全可以将 不等式变为等式
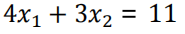
2. 地标为C(X1,X2)当求C的时候可以从图中看出X1是0,
3. 然我们一开始没有图,可以假设为0,这样就可以求出X2的值,这样C(0,X2)的地表就出来了,
4. D地标求法同理,假设X2=0,这样就是可以求出X1的值,后D(X1,0)的地标就出来了,
5. 根据这两个点就可以画出可行区域的C点到D点的线
4. 然后就可以 获取到黑色区域 的可行区域和交叉点E点的最优值地表 E(X1,X2)
5. 将最优值 E的𝑥1和X2代入总利润的二元一次方程 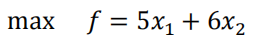中 ,解出总利润最大值16万元 

 

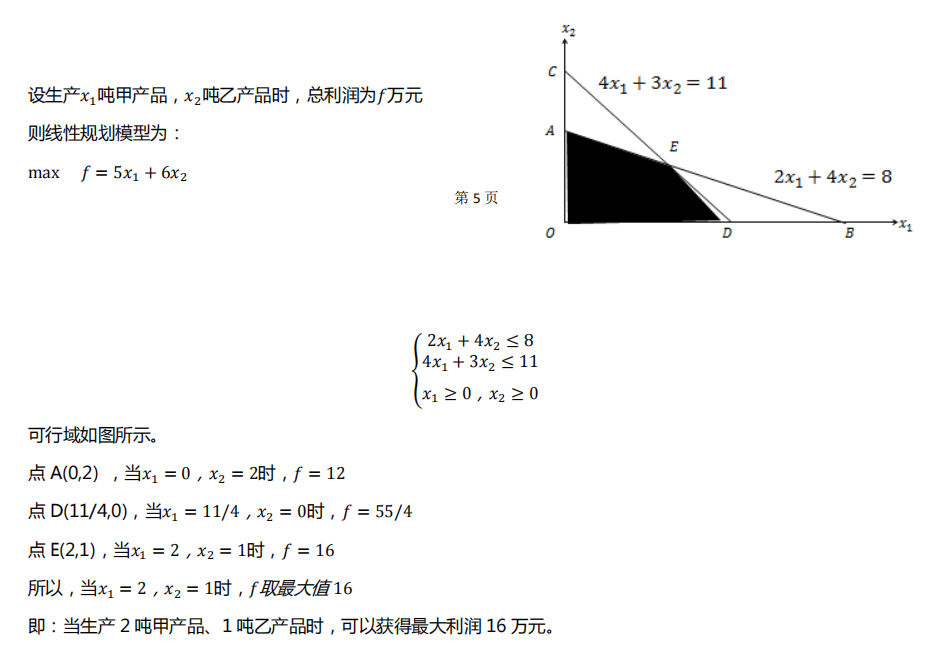
解题过程

 

 

 

 

 

答案也可以写成这样