数据结构系列(4)之 B 树
本文将主要讲述另一种树形结构,B 树;B 树是一种多路平衡查找树,但是可以将其理解为是由二叉查找树合并而来;它主要用于在不同存储介质之间查找数据的时候,减少 I/O 次数(因为一次读一个节点,可以读取多个数据);
一、结构概述
B 树,多路平衡查找树,即有多个分支的查找树;如图所示:
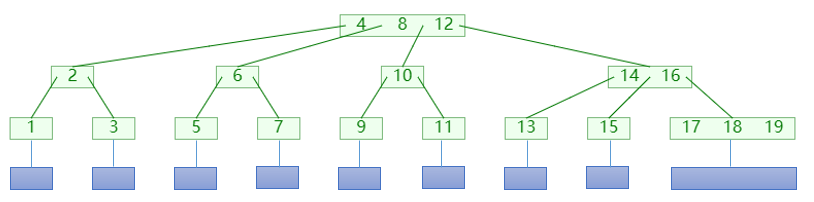
B 树主要应用于多级存储介质之间的查找,图中的蓝色节点为外部节点,代表下一级存储介质;绿色节点则为内部节点;同时我们将B 树按照其最大分支树进行分类,比如图中的则为4 阶B 树;
对于 m 阶 B 树(m >= 2):
- 外部节点的深度统一相等,叶子节点的深度统一相等,树高等于外部节点深度;
- 内部节点不超过(m-1)个关键码,不超过 m 路分支,同时不少于(⌈m /2⌉)路分支,但是根节点最少一路分支即可;
- 所以 m 阶 B 树又称为(⌈m /2⌉,m)树;
public class BTree<E extends Comparable<? super E>> implements Iterable<E> {
private Node<E> root;
private final int order;
private final int MAX_KEYS;
private final int MIN_KEYS;
private int height;
private int totalSize;
final class Node<T> {
Object[] values;
Node<T>[] children;
Node<T> parent;
boolean isLeaf;
int size;
Node() {
this.values = new Object[order]; // 实际只有order-1个关键码,超出时会分裂;
this.children = new Node[order + 1]; // 同样+1;
this.isLeaf = true;
this.size = 0;
}
}
}
二、节点修复
因为B 树节点的在[ ⌈m/2⌉ - 1, m -1 ]之间,所以在动态插入和删除的过程中一定会发生不平衡,下面将介绍修复不平衡的几种方法;
1. 分裂
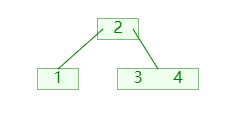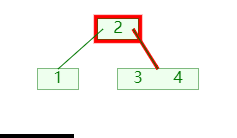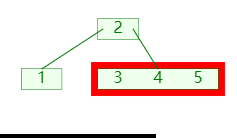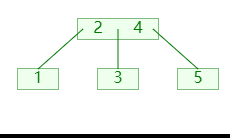
插入时当节点的关键码超过 m-1 ,就将大节点分为两个小节点;如图:
分裂时:
- 将第
⌊m/2⌋个关键码移入父节点; - 分成的两个节点,则成为新关键码的左右孩子节点;(需要新增节点,并移动节点信息);
- 再递归的检查其父节点的关键码是否超过;
实现:
private void split(Node<E> p) {
Node<E> parent = p.parent;
if (parent == null) { // parent为null,即当前节点为root,需要上升高度(唯一会导致树高度增加的操作)
parent = new Node<E>();
parent.isLeaf = false; // 设置为非叶子节点
root = parent; // 更新root节点
height++; // 高度加1
}
int mid = (p.size - 1) >>> 1; // 需要上一的关键码
Node<E> left = new Node<E>(); // 分裂,创建一个新的空节点
Node<E> right = p; // 右边节点为原来的节点
left.isLeaf = p.isLeaf; // 节点是否叶子,取决于分裂前是否叶子。
// 更新孩子节点的parent指针
if (!p.isLeaf) {
for (int i = 0; i <= mid; ++i) { // 左子树的孩子应该指向左子树。
p.children[i].parent = left;
}
}
parent.insertToNonLeaf((E) p.values[mid], left, right); // 把中间节点插入父节点。
int i, j;
// 拷贝右子树信息到左子树。
for (i = 0; i < mid; ++i) {
left.values[i] = right.values[i];
left.children[i] = right.children[i];
}
left.children[i] = right.children[mid];
left.size = mid; // 更新左子树关键字数量
// 删除右子树多余关键字和孩子,因为已经拷贝到左孩子中去了。
for (i = mid + 1, j = 0; i < right.size; ++i, ++j) {
right.values[j] = right.values[i];
right.children[j] = right.children[i];
}
right.children[j] = right.children[right.size]; // 更新最后一个孩子节点, 注意奇数j == mid,但偶数不是。。
right.size = right.size - mid - 1; // 更新右子树关键字数量
left.parent = parent; // 把子树的父亲节点更新
right.parent = parent;
if (parent.size > MAX_KEYS) // 如果父亲节点也达到最大关键字数量,需要递归分裂。
split(parent);
}
int insertToNonLeaf(T key, Node<T> left, Node<T> right) {
int index = insertIndex(key);
if (index < 0) return index;
for (int i = size; i > index; --i) {
values[i] = values[i - 1];
children[i + 1] = children[i];
}
children[index] = left;
children[index + 1] = right;
values[index] = key;
size++;
return index;
}
2. 旋转
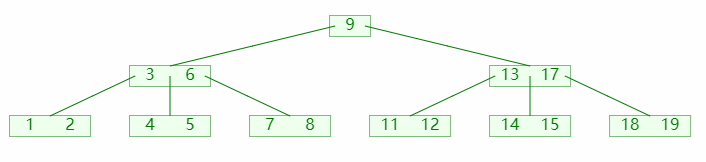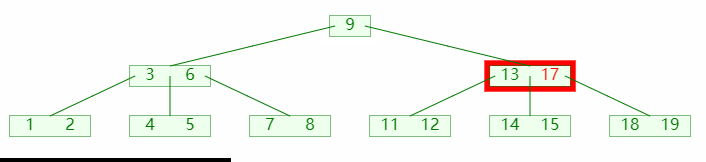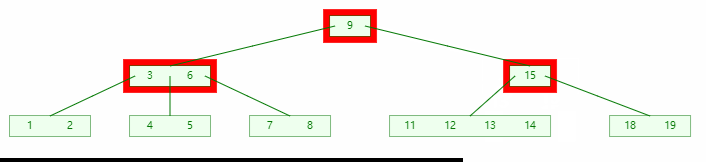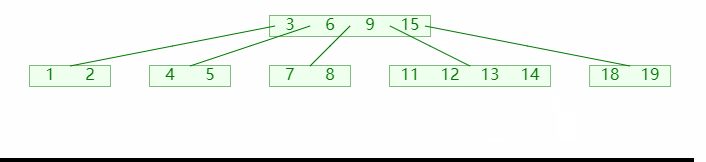
删除节点时,可能会导致节点的关键码数量小于 ⌊m/2⌋,此时可以向他的左孩子或者右孩子,借一个关键码;如图:
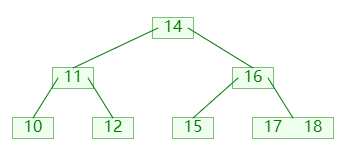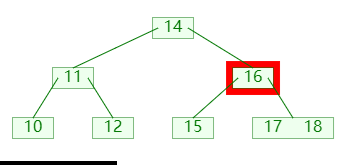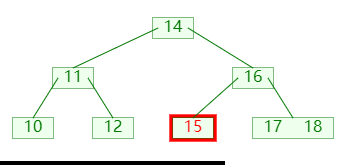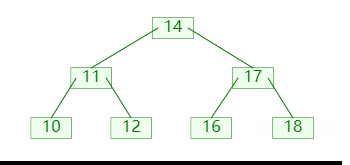
图中:
- 首先检查发现没有左兄弟,并且右兄弟可以借出
- 然后左旋转父节点,父节点的关键码进入补齐,右兄弟的关键码进入父节点;
右孩子富裕时左旋:
private void leftRotate(Node<E> p) {
Node<E> right = rightSibling(p); // 获取右兄弟
int myRank = rankInChildren(p); // 获取在父节点中的秩
Object oldSeparator = p.parent.values[myRank];
p.values[p.size] = oldSeparator;
p.size++;
Object newSeparator = right.values[0];
Node<E> child = right.isLeaf ? null : right.children[0]; // 获取右兄弟中最小的关键码
int i;
for (i = 0; i < right.size - 1; ++i) {
right.values[i] = right.values[i + 1];
if (!right.isLeaf)
right.children[i] = right.children[i + 1];
}
if (!right.isLeaf) {
right.children[right.size - 1] = right.children[right.size];
child.parent = p;
p.children[p.size] = child;
}
right.size--;
p.parent.values[myRank] = newSeparator;
}
private Node<E> rightSibling(Node<E> p) {
if (p == null || p.parent == null) // 根节点无兄弟节点
return null;
Node<E> parent = p.parent;
int i = rankInChildren(p);
if (i >= 0 && i < parent.size) {
return parent.children[i + 1];
}
return null;
}
左孩子富裕时右旋:
private void rightRotate(Node<E> p) {
Node<E> left = leftSibling(p);
int myRank = rankInChildren(p);
Object oldSeparator = p.parent.values[myRank - 1];
Node<E> child = null;
if (!left.isLeaf) {
child = left.children[left.size];
p.children[p.size + 1] = p.children[p.size];
}
for (int i = p.size; i >= 1; --i) {
p.values[i] = p.values[i - 1];
if (!p.isLeaf)
p.children[i] = p.children[i - 1];
}
if (!left.isLeaf) {
child.parent = p;
p.children[0] = child;
}
p.values[0] = oldSeparator;
p.size++;
Object newSeparator = left.values[left.size - 1];
left.size--;
p.parent.values[myRank - 1] = newSeparator;
}
private Node<E> leftSibling(Node<E> p) {
if (p == null || p.parent == null) return null;
Node<E> parent = p.parent;
int i = rankInChildren(p);
if (i >= 1) return parent.children[i - 1];
return null;
}
3. 合并
当左右孩子的关键码都不足以借出时,则将两个孩子合并,如图:
图中:
- 首先左右兄弟都不足以借出
- 从父节点借得一个关键码;
- 然后以借得的关键码为粘合左右兄弟节点;
- 最后需要检查父节点是否平衡;
实现:
private void merge(Node<E> p) {
Node<E> parent = p.parent;
assert (parent != null);
Node<E> left = p; // left node 或者是当前节点,即贫困节点,或者是当前节点的左兄弟节点。
Node<E> right = rightSibling(p);
if (right == null) {
left = leftSibling(p);
right = p;
}
int myRank = rankInChildren(left);
// 把父亲节点的Separator下移到需要合并的节点left
Object separator = parent.values[myRank];
left.values[left.size] = separator;
left.size++;
// 从父亲节点中删除Separator
for (int i = myRank; i < parent.size - 1; i++) {
parent.values[i] = parent.values[i + 1];
parent.children[i + 1] = parent.children[i + 2];
}
//FIXME
parent.values[parent.size - 1] = null;
parent.children[parent.size] = null;
parent.size--;
// 拷贝右节点到左节点
for (int i = 0; i < right.size; ++i) {
left.size++;
left.values[left.size - 1] = right.values[i];
if (!left.isLeaf) {
right.children[i].parent = left; // donot forget it.
left.children[left.size - 1] = right.children[i];
}
}
// 不要忘记最后一个孩子更新。
if (!left.isLeaf) {
right.children[right.size].parent = left;
left.children[left.size] = right.children[right.size];
}
// 如果父亲节点也贫困了,需要从父亲节点重新调整,直到满足平衡或者父亲节点就是root节点
if (parent.size < MIN_KEYS) {
if (parent.size == 0 && parent == root) {
root = left;
root.parent = null;
height--;
} else {
rebalancingAfterDeletion(parent);
}
}
}
三、查找
查找时采取逐层查找:
- 查找不大于目标关键码的最大值;
- 精确对比是否命中,若没有命中则深入孩子节点
实现:
public Node<E> search(E e) {
Node<E> v = root;
while (v != null) { // 逐层查找
int r = v.search(e); // 在当前节点中,找到不大于e的最大关键码
if (r >= 0 && cmp(e, v.values[r]) == 0) {
return v;
}
v = v.children[r + 1]; // 转入对应子树——需做I/O,最费时间
}
return null;
}
int search(T key) {
int low = 0;
int high = size - 1;
do {
int mi = (low + high) >> 1;
if (cmp(key, values[mi]) < 0) {
high = mi;
} else {
low = mi + 1;
}
} while (low < high);
return --low;
}
四、插入
public boolean add(E key) {
if (key == null) {
return false;
}
if (root == null) {
root = new Node<E>();
this.height = 1;
this.totalSize = 0;
}
boolean inserted = insert(key, root);
if (inserted) {
++totalSize;
++modCount;
return true;
} else {
return false;
}
}
private boolean insert(E key, Node<E> p) {
assert (p != null);
if (!p.isLeaf) { // 总是插入到叶子中,不可能直接插入到内部节点
int index = p.insertIndex(key); // 获取插入位置,如果 < 0说明已存在
if (index < 0) // index < 0 说明key已存在
return false;
return insert(key, p.children[index]); // 插入的位置就是孩子的位置
}
boolean inserted = p.insertToLeaf(key) >= 0; // p是叶子节点,直接插入。
if (p.size > MAX_KEYS) { // 如果关键字多于最大关键字数量,需要分裂节点。
split(p);
}
return inserted;
}
int insertToLeaf(T key) {
int index = insertIndex(key);
if (index < 0)
return index;
for (int i = size; i > index; --i) {// 移动向右key
values[i] = values[i - 1];
}
values[index] = key;
++size;
return index;
}
五、删除
public boolean remove(E e) {
if (root == null) {
return false;
}
boolean isRemoved = remove(e, root);
if (isRemoved) {
--totalSize;
++modCount;
}
return isRemoved;
}
private boolean remove(E e, Node<E> p) {
if (p.isLeaf) { // 删除的关键字在叶子节点中,直接删除,然后重新调整
boolean isRemoved = p.deleteFromLeaf(e);
if (p.size < MIN_KEYS) {
rebalancingAfterDeletion(p); // rebalances the tree
}
return isRemoved;
}
int index = p.binarySearch(e);
if (index < 0) { // 不在吃节点中,递归从子树中查找。
return remove(e, p.children[-index - 1]); // -index - 1就是插入位置,即孩子节点位置。
}
// 删除的是内部节点,需要寻找左子树最大节点(或者右子树中最小节点)作为新分隔符替换删除的关键字。
Node<E> leftLeaf = leftLeaf(p, index);// 寻找左子树最右节点。
Object candidate = leftLeaf.values[leftLeaf.size - 1];
//从叶子节点中移除候选节点
leftLeaf.values[leftLeaf.size - 1] = null;
leftLeaf.size--;
//候选节点作为分隔符替代删除的节点。
p.values[index] = candidate;
//重新调整树使其平衡。
if (leftLeaf.size < MIN_KEYS) {
rebalancingAfterDeletion(leftLeaf);
}
return true;
}
boolean deleteFromLeaf(T key) {
int index = binarySearch(key);
if (index < 0)
return false;
for (int i = index; i < size; ++i) {
values[i] = values[i + 1];
}
this.size--;
return true;
}
private void rebalancingAfterDeletion(Node<E> p) {
if (p == root) { // 说明p是root节点,不需要处理
return;
}
Node<E> left = leftSibling(p); // 获取左兄弟
if (left != null && left.size > MIN_KEYS) { // 左兄弟很富裕, 右旋转。
rightRotate(p);
return;
}
Node<E> right = rightSibling(p); // 右兄弟
if (right != null && right.size > MIN_KEYS) { // 如果右兄弟节点富裕,左旋转。
leftRotate(p);
return;
}
merge(p);
}
总结
- 通常情况下B 树节点的大小设置会和缓存页相当,以保证一次能够获取更多的关键码,以减少 I/O;
- B 树仍然还有很多的变种,甚至红黑树也和(2,4)B 树息息相关,后面的章节会继续讲到;

