数据结构——树

一、树的基本概念

1、树的定义
树（Tree）是n（n≥0）个节点的有限集合T，它满足两个条件 ：有且仅有一个特定的称为根（Root）的节点；其余的节点可以分为m（m≥0）个互不相交的有限集合T1、T2、……、Tm，其中每一个集合又是一棵树，并称为其根的子树（Subtree）。
2、树的基本概念
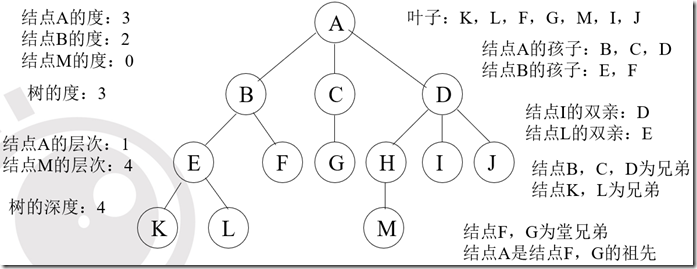
a、一个节点的子树的个数称为该节点的度数，一棵树的度数是指该树中节点的最大度数。
b、度数为零的节点称为树叶或终端节点，度数不为零的节点称为分支节点，除根节点外的分支节点称为内部节点。
c、一个节点的子树之根节点称为该节点的子节点，该节点称为它们的父节点，同一节点的各个子节点之间称为兄弟节点。一棵树的根节点没有父节点，叶节点没有子节点。
d、一个节点系列k1,k2,…,ki,ki+1,…,kj,并满足ki是ki+1的父节点，就称为一条从k1到kj的路径，路径的长度为j-1,即路径中的边数。路径中前面的节点是后面节点的祖先，后面节点是前面节点的子孙。
e、节点的层数等于父节点的层数加一，根节点的层数定义为一。树中节点层数的最大值称为该树的高度或深度。
f、若树中每个节点的各个子树的排列为从左到右，不能交换，即兄弟之间是有序的，则该树称为有序树。一般的树是有序树。
g、m（m≥0）棵互不相交的树的集合称为森林。树去掉根节点就成为森林，森林加上一个新的根节点就成为树。

3、树的逻辑结构
树中任何节点都可以有零个或多个直接后继节点（子节点），但至多只有一个直接前趋节点（父节点），根节点没有前趋节点，叶节点没有后继节点。

二、二叉树

1、二叉树的概念
二叉树（Binary Tree）是n（n≥0）个节点的有限集合，它或者是空集（n＝0），或者是由一个根节点以及两棵互不相交的、分别称为左子树和右子树的二叉树组成。二叉树与普通有序树不同，二叉树严格区分左孩子和右孩子，即使只有一个子节点也要区分左右。

2、二叉树的性质
二叉树第i（i≥1）层上的节点最多为2的i-1次方个。
深度为k（k≥1）的二叉树最多有2的k次方－1个节点。
在任意一棵二叉树中，树叶的数目比度数为2的节点的数目多一。
总节点数为各类节点之和：n = n0 + n1 + n2 
总节点数为所有子节点数加一：n = n1 + 2*n2 + 1
故得：n0 = n2 + 1 ;

3、满二叉树和完全二叉树
满二叉树 ：深度为k（k≥1）时有2k－1个节点的二叉树。
完全二叉树 ：只有最下面两层有度数小于2的节点，且最下面一层的叶节点集中在最左边的若干位置上。
具有n个节点的完全二叉树的深度为：（log2n）＋1或『log2(n+1)。

4、二叉树的顺序存储
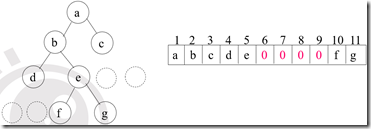
若二叉树不是完全二叉树，通过补虚节点，将其补成完全二叉树。
按从上到下，从左到右的顺序编号，根节点为1
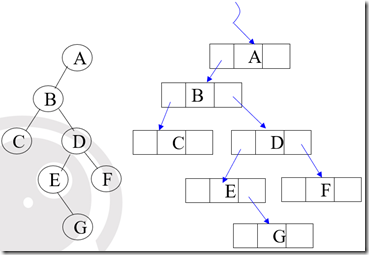
按编号一次存储在连续空间中，虚节点用特殊符号标识即可。

5、二叉树的链式存储

6、二叉树的遍历
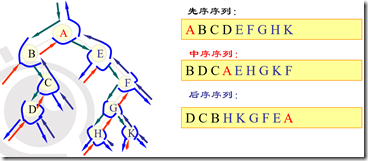
遍历 ：沿某条搜索路径周游二叉树，对树中的每一个节点访问一次且仅访问一次。
“遍历”是任何类型均有的操作，对线性结构而言，只有一条搜索路径(因为每个结点均只有一个后继)，故不需要另加讨论。而二叉树是非线性结构，每个结点有两个后继，则存在如何遍历即按什么样的搜索路径进行遍历的问题。
由于二叉树的递归性质，遍历算法也是递归的。
三种基本的遍历算法：先上后下的按层次遍历；先左（子树）后右（子树）的遍历；先右（子树）后左（子树）的遍历。