DP斜率优化总结
DP斜率优化总结
任务安排1
首先引入一道题,先\(O(N^2)\)做法:分别预处理出\(T_i,C_i\)前缀和\(t[i],c[i]\),设\(f[i]\),其中\(f[i]\)并不表示前\(i\)个任务花费的时间,而是壳含前面所有决策对于后面的影响。这道题dp思路就是边决策边加上当前决策对于后面的影响(一种“费用提前计算”的思想)
转移方程:
#include <cstdio>
#include <cstring>
#define MIN(A,B) ((A)<(B)?(A):(B))
#define MAXN 5005
using namespace std;
int f[MAXN];
int sumt[MAXN],sumc[MAXN];
int n,s;
int main(){
memset(f, 0x3f, sizeof(f));
f[0]=0;
scanf("%d\n%d", &n, &s);
for(int i=1;i<=n;++i){
int t,c;
scanf("%d %d", &t, &c);
sumt[i]=sumt[i-1]+t;
sumc[i]=sumc[i-1]+c;
}
for(int i=1;i<=n;++i)
for(int j=0;j<i;++j){
f[i]=MIN(f[j]+(sumc[i]-sumc[j])*sumt[i]+s*(sumc[n]-sumc[j]), f[i]);
}
printf("%d", f[n]);
return 0;
}
任务计划2
斜率优化做法。将原转移方程移项,让只含\(j\)的式子移到左边,其余移到右边,再将右边含\(j\)的式子提公因式,得到
此时将外层循环到的\(i\)看做已知量(则关于\(i\)的变量\(t[i],c[i]\)为常数),看做一个斜率确定的一次函数\(y=kx+b\),其中\(f[j]\)看做函数的\(y\),\(c[j]\)看做函数的\(x\),\((t[i]+s)\)为斜率。要让\(f[i]\)最小即让此一次函数截距最小。
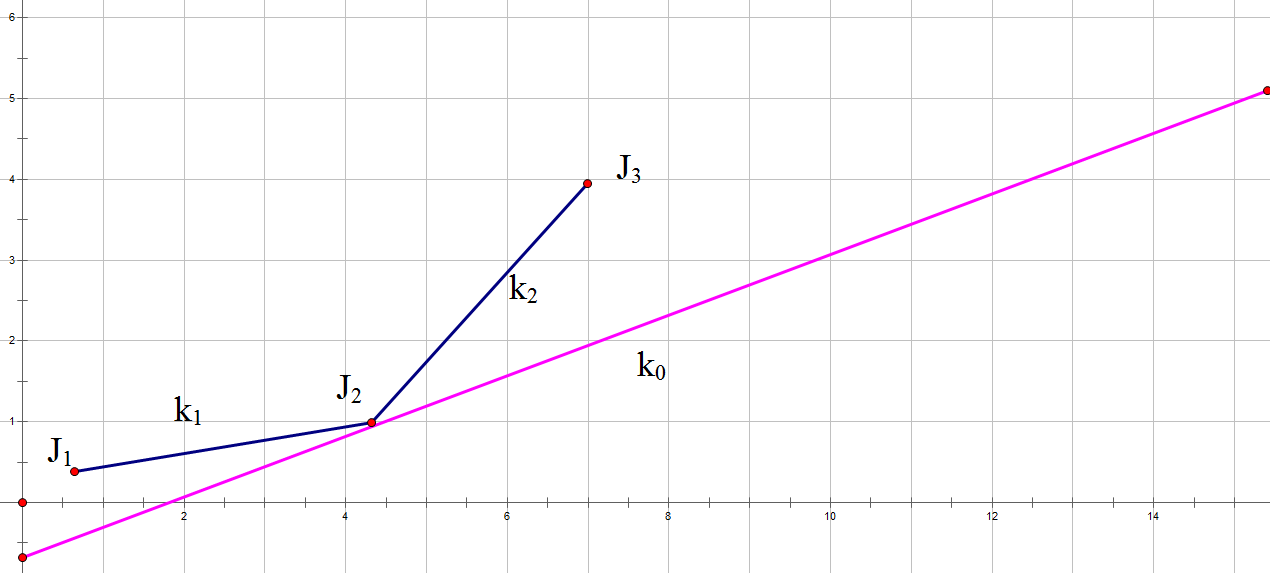
(图自ButterflyDew)
而容易得到:将此确定的斜率函数从最下面向上平移遇到的第一个点\((c[j],f[j])\)就是能取到最小截距(最优\(f[i]\))的点,(满足\(k_1\le k_0\le k_2\)),如图,也就是一个下凸壳的顶点。
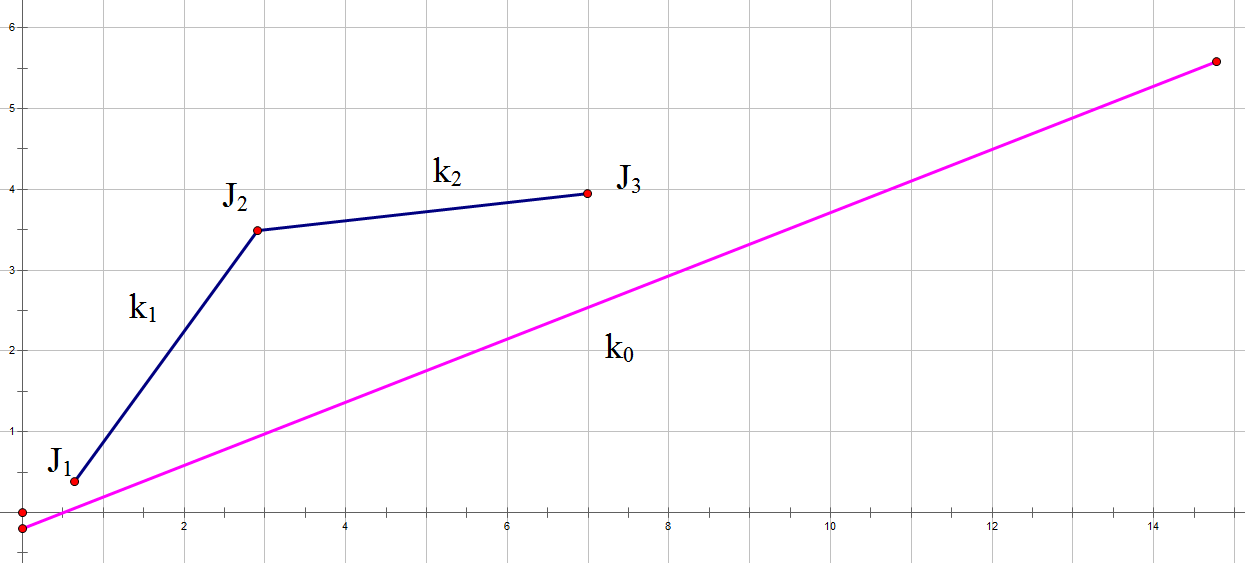
而像这样的上凸壳顶点如图显然一定不会是最优解,所以我们维护一个下凸壳,每次找到顶点即为最优。
而这道题我们不需要维护整个下凸壳,而只维护下凸壳顶点及顶点右侧的点(因为左侧不可能比顶点优)。我们维护一个单调队列,使队首为下凸壳顶点,每次最优即为队首元素。维护时先将下凸壳顶点左边的所有点弹掉(若当前点与下一个点构成的直线斜率小于等于\(s+t[i]\),则当前点在左边),之后队首就是下凸壳的顶点,取出并算出的\(f[i]\)即为最优,最后再将所有构成上凸壳的点删去维护一下下凸壳。
单调队列部分实现代码:
while(l<r&&f[q[l+1]]-f[q[l]]<=(S+t[i])*(c[q[l+1]]-c[q[l]])) l++; // 弹出顶点左边的点
f[i]=f[q[l]]+t[i]*c[i]+S*c[n]-c[q[l]]*(S+t[i]);
while(l<r&&(f[i]-f[q[r]])*(c[q[r]]-c[q[r-1]])<=(f[q[r]]-f[q[r-1]])*(c[i]-c[q[r]])) r--; // 维护下凸壳
q[++r]=i;
完整代码:
#include <cstdio>
#include <cstring>
#define MIN(A,B) ((A)<(B)?(A):(B))
#define MAXN 5005*2
using namespace std;
int f[MAXN],q[MAXN];
int t[MAXN],c[MAXN];
int n,s;
int main(){
memset(f, 0x3f, sizeof(f));
f[0]=0;
scanf("%d\n%d", &n, &s);
for(int i=1;i<=n;++i){
int tt,tc;
scanf("%d %d", &tt, &tc);
t[i]=t[i-1]+tt;
c[i]=c[i-1]+tc;
}
int l=1,r=1;
for(int i=1;i<=n;++i){
while(l<r&&(f[q[l+1]]-f[q[l]])<=(t[i]+s)*(c[q[l+1]]-c[q[l]])) l++;
f[i]=f[q[l]]-c[q[l]]*(t[i]+s)+s*c[n]+c[i]*t[i];
while(l<r&&(f[q[r]]-f[q[r-1]])*(c[i]-c[q[r]])>=(f[i]-f[q[r]])*(c[q[r]]-c[q[r-1]])) r--;
q[++r]=i;
}
printf("%d", f[n]);
return 0;
}
任务安排3
因为\(T_i\)可能为负数,所以直线斜率\(s+t[i]\)不单增,所以不能直接单调队列取队首,而是二分查找出两条斜率为\(k_1,k_2\)的直线满足\(k_1\le s+t[i]\le k_2\),两条直线交点即为最优点。
#include <cstdio>
#include <cstring>
#define MIN(A,B) ((A)<(B)?(A):(B))
#define MAXN 300003
#define ll long long
using namespace std;
ll f[MAXN];
int q[MAXN];
ll t[MAXN],c[MAXN];
int n,s;
int l=1,r=1;
inline int query(ll k){
int L=l,R=r,ans;
while(L<=R){
int mid=(L+R)>>1;
if((f[q[mid]]-f[q[mid-1]])<=k*(c[q[mid]]-c[q[mid-1]])) L=mid+1,ans=mid;
else R=mid-1;
}
return q[ans];
}
int main(){
memset(f, 0x3f, sizeof(f));
f[0]=0;
scanf("%d\n%d", &n, &s);
for(int i=1;i<=n;++i){
ll tt,tc;
scanf("%lld %lld", &tt, &tc);
t[i]=t[i-1]+tt;
c[i]=c[i-1]+tc;
}
for(int i=1;i<=n;++i){
int j=query(t[i]+s);
f[i]=f[j]-c[j]*(t[i]+s)+s*c[n]+c[i]*t[i];
while(l<r&&
(f[q[r]]-f[q[r-1]])*(c[i]-c[q[r]])>=(f[i]-f[q[r]])*(c[q[r]]-c[q[r-1]])) r--;
q[++r]=i;
}
printf("%lld", f[n]);
return 0;
}
百日旅行
\(N\)天,如果连续\(x\)天旅游,则花费\(p\times x\times x\),否则连续\(x\)天吃饭,花费\(Q\times x\),问最小花费
设计dp,\(f[i]\)表示第\(i\)天最小花费并且这一天在旅游,\(g[i]\)表示在这一天吃饭,转移方程:
f[i]=min(g[j]+SQR(i-j)*p,f[i])
g[i]=min(f[j]+(i-j)*q,g[i])
观察\(g[i]\),\(g[i]=i*q+f[j]-j*q\),所以维护\(1\)到\(i-1\)的\(f[i]-i*p\)最小值即可。
观察\(f[i]\),\(f[i]=g[i]+p*i^2-2*p*i*j+p*j^2\)
移项,使只含\(j\)的式子在左边,其余右边,得\(g[j]+p*j^2=i*(2*p*j)+f[i]-p*i^2\)
此时看做一个一次函数,\(x=2*p*j,k=i,b=f[i]-p*i^2\),要想\(f[i]\)最小,即让截距最小,维护一个下凸壳。又发现斜率\(i\)单增,可使用单调队列。
#include <cstdio>
#include <algorithm>
#define ll long long
#define MAXN 200002
#define MIN(A,B) ((A)<(B)?(A):(B))
#define j (q[l])
#define SQR(A) ((A)*(A))
#define Y(A) (g[A]+P*(A)*(A))
#define X(A) ((A)*2*P)
using namespace std;
int n,l,r;
ll f[MAXN],g[MAXN],q[MAXN],P,Q;
int main(){
scanf("%d %lld %lld", &n, &P, &Q);
l=1,r=1;
ll t=0;
for(int i=1;i<=n;++i){
while(l<r&&(Y(q[l + 1]) - Y(q[l])) <= i*(X(q[l+1]) - X(q[l]))) ++l;
f[i]=g[j]+P*SQR(i-j);
g[i]=i*Q+t;
t=min(f[i]-i*Q,t);
while(l<r && (Y(q[r]) - Y(q[r-1])) * (X(i) - X(q[r])) >= (Y(i) - Y(q[r])) * (X(q[r]) - X(q[r-1]))) --r;
q[++r]=i;
}
printf("%lld", min(f[n], g[n]));
return 0;
}
/*
g[i]=i*q+f[j]-j*q
g[j]+p*j^2=i*(2*p*j)+f[i]-p*i^2
*/

