拉格朗日乘数法

在解决优化问题时，经常会用到拉格朗日乘数法，

举一个简单的例子，f(x)=x²+y²,约束条件为h(x,y)=x+y-1=0,这个例子非常简单，简单到不需要使用拉格朗日乘数法来解决。

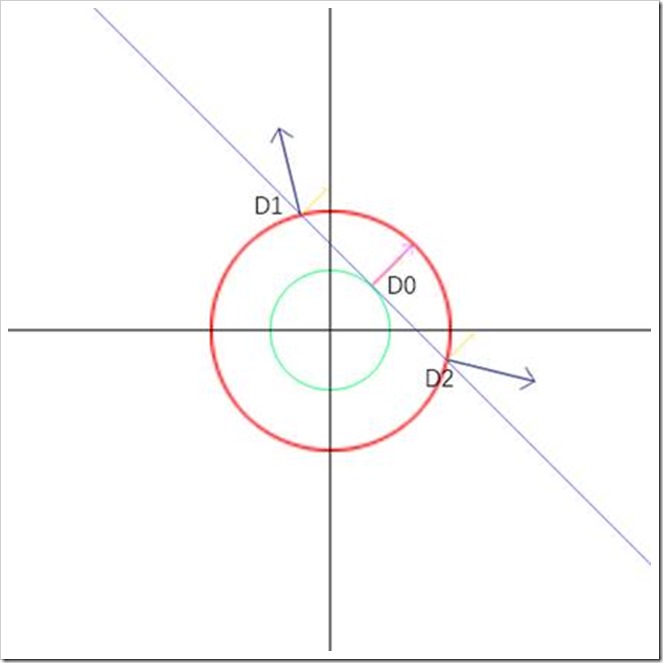
图只是示意一下，请忽略比例不对的地方，红色和绿色的线是目标函数的等高线，蓝色线是约束条件，其他带箭头的线表示法线。

很显然，D0是所求的最优解，我们来分析一下D0有什么特点呢？

1. D0位于约束曲线上（本例中是直线），即h(x,y)=0，但是约束曲线上所有点都满足这一要求，因此仅仅这个要求并不充分，D1,D2同样位于曲线上，它们与D0有什么区别呢？
2. D0所在的等高线与曲线相切，也就是说等高线的法线方向平行于曲线的法线方向，即f’(x,y)= -λh’(x,y)，或者f’(x,y)- λh’(x,y)=0，两种表示方式是等价的，为了能够更方便的推出拉格朗日乘数法，采用后一种表示方式。f’(x,y)- λh’(x,y)=0，也就是∂f/∂x-λ∂h/∂x=0，∂f/∂y-λ∂h/∂y=0

满足以上两个要求的点一定是最优解。总结以上分析，得出最优点需要满足以下要求:

h(x,y)=0

∂f/∂x-λ∂h/∂x=0

∂f/∂y-λ∂h/∂y=0

接下来构造拉格朗日函数，L(λ,x,y) = f(x,y) +λ*h(x,y)

分别对λ,x,y求偏导，并使其等于0，即可以得到上面的3个式子。