201971010150-闫雨馨 实验三 结对实验 《{0-1}KP 实例数据集算法实验平台》
| 项目 | 内容 |
|---|---|
| 课程班级博客链接 | 2019级卓越工程师班 |
| 这个作业要求链接 | 实验三 软件工程结对项目 |
| 我的课程学习目标 | 1.提高软件项目开发中合作能力 2.提高代码编程能力 |
| 这个作业在哪些方面帮助我实现学习目标 | 1.体验软件项目开发中的两人合作,练习结对编程(Pair programming) 2.掌握Github协作开发软件的操作方法 |
| 结对方学号-姓名 | 201971010223-刘温元 |
| 结对方本次博客作业链接 | 结对方博客 |
| 本项目Github的仓库链接地址 | Github仓库 |
- 任务一完成情况说明:
阅读《现代软件工程—构建之法》第3-4章内容,理解并掌握代码风格规范、代码设计规范、代码复审、结对编程概念。
1.《现代软件工程—构建之法》第3章内容知识总结- IC在团队中的流程:
- 通过交流、实验、快速原型等方法,理解问题、需求或任务
- 提出多种解决办法并估计工作量
其中包括寻找以前的解决方案,因为很多工作是重复性的- 与相关角色交流解决问题的提案,决定一个可行的方案
- 执行,把想法变成实际中能工作的代码,同时验证方案的可行性和其他特性(例如程序的效能等)
- 和团队的其他角色合作,在测试环境中测试实现方案,修复缺陷(Bug)。如果此方案有严重的问题,那么久考虑其他方案
- 在解决方案发布出去之后,对结果负责
- TSP对团队成员也有要求:
1.交流:能有效地和其他队员交流,从大的技术方向,到看似微小的问题
2.说到做到:就像上面说到“按时交付”
3.接受团队赋予的角色并按角色要求工作:团队要完成任务,有很多事情要做,是否能接受不同的任务并高质量完成
4.全力投入团队的活动:就像一些评审会议,代码复审,就要全力以赴地参加,而不是游离于团队之外
5.按照团队流程的要求工作:团队有自己的流程,个人的能力即使,也要按照团队制定的流程工作,而不要认为自己不受流程约束
6.准备:在开会讨论之前,开始一个新功能之前,一个新项目之前,都要做好准备工作。
7.理性地工作:软件开发有很多个人的、感情驱动的因素,但是一个成熟的团队成员必须从事实和数据出发,按照流程,理性地工作。很多人认为自己需要灵感和激情,才能为宏大的目标奋斗,才能成为专业人士。著名的艺术家Chuck Close说:我总觉得灵感是属于业余爱好者的。我们职业人士只是每天持续工作。今天你继续昨天的工作,明天你继续今天的工作,最终你会有所成就
2.《现代软件工程—构建之法》第4章内容知识总结
- 代码风格规范:
主要是文字上的规定。代码风格的原则是:简明、易读、无二义性,包括对于缩进、行宽、括号、分行、命名、下划线、注释、大小写以及断行与空白的{}行的处理,具体如下:
- 缩进:可以使用Tab键以及2、4、8等空格。个人认为依据不同是编程语言,可以使用不同的缩进方式。
- 行宽:以前的计算机/打字机显示行宽为80字符,现在可以限定为100字符。
- 括号:用括号清楚的表明逻辑优先级。
- 断行与空白的{}行:主要是在多层循环中规范使用。
- 分行:不要把多条语句放在一行上。
- 命名:命名能够表明变量的类型及相应的语义,简洁易懂。
- 下换线:合理使用来分隔变量名字中的作用域标注和变量的语义。
- 大小写:多个单次组成的变量名,用大小写区分,例如著名的驼峰式命名法。
- 注释:能够很好的解释程序是做什么的,以及为什么这样做。
- 代码设计规范:
不光是程序书写格式的问题,而且牵涉到程序设计、模块之间的关系、设计模式等的方方面面,主要有以下几个部分:
- goto:函数最好有单一的出口,可以使用goto。
- 函数:能够很好的完成一件事。
- c++类的处理:注意类、classvc.struct、公共/保护/私有成员、数据成员、虚函数、构造函数、析构函数、new和delete、运算符、异常处理、类型继承等的规范设计。
- 错误处理:预留足够的时间,使用的方法包括参数处理和断言。
- 断言:使用断言来验证正确性。
- 参数处理:在debug版本中,所有的参数都要验证其正确性。在正式版本中,对从外部(用户或别的模块)传递过来的参数,要验证其正确性。
- 数据成员:数据类型的成员用m_ name说明。不要使用公共的数据成员,要用inline访问函数,这样可兼顾封装和效率。
- 构造函数:不要在构造函数中做复杂的操作,简单初始化所有数据成员即可。构造函数不应该返回错误(事实上也无法返回)。把可能出错的操作放到HrInit()或FInit()中。
- 异常:异常是在“异乎寻常”的情况下出现的,它的设置和处理都要花费“异乎寻常”的开销,所以不要用异常作为逻辑控制来处理程序的主要流程。了解异常及处理异常的花销,在C++语言中,这是不可忽视的开销。当使用异常时,要注意在什么地方清理数据。异常不能跨过DLL或进程的边界来传递信息,所以异常不是万能的。
- 运算符:在理想状态下,我们定义的类不需要自定义操作符。确有必要时,才会自定义操作符。运算符不要做标准语义之外的任何动作。运算符的实现必须非常有效率,如果有复杂的操作,应定义一个单独的函数。当你拿不定主意的时候,用成员函数,不要用运算符。
- 代码复审:
看代码是否在代码规范的框架内正确地解决了问题。代码复审的三种形式:自我复审、同伴复审、团队复审。
- 自我复审:用同伴复审的标准来要求自己。不一定最有效, 因为开发者对自己总是过于自信。如果能持之以恒,则对个人有很大好处。
- 同伴复审:简单易行。
- 团队复审:有比较严格的规定和流程,适用于关键的代码,以及复审后不再更新的代码。覆盖率高——有很多双眼睛盯着程序,但效率可能不高。
- 结对编程
指一起分析,一起设计,一起写测试用例,一起做单元测试,一起做集成测试,一起写文档等等。
- 角色:驾驶员:控制键盘输入;领航员:起到领航、提醒的作用。
- 好处:在开发层次,可以提供更好的设计质量和代码质量,两人合作解决问题的能力更强;对开发人员,带来更多的信心,高质量的产出带来更高的满足感;企业管理层次上,有效地交流,相互学习和传递经验,分享知识,取得更高的投入产出比。
- 好处:每人在各自独立设计、实现软件的过程中不免要犯这样那样的错误。在结对编程中,因为有随时的复审和交流,程序各方面的质量取决于一对程序员中各方面水平较高的那一位。这样,程序中的错误就会少得多,程序的初始质量会高很多,这样会省下很多以后修改、测试的时间。
- 任务二完成情况说明:
| 项目成果评价 | 内容 |
|---|---|
| 结对方 | 201971010223-刘温元 |
| 结对方实验二博客作业链接 | 对方博文链接 |
| 结对方实验二的Github的仓库链接地址 | 仓库链接 |
- 对项目博文作业进行阅读并进行评论
- 博客结构:
博文整体排版较好,清晰可读,但是在内容上应该改进,更加详细一点。- 博文内容:
实验内容完成度不错,基本实现了实验二中的要求,并对需求分析、功能设计及设计实现设计实现都进行了详细的称述。- 博文结构与PSP中“任务内容”列的关系:
博文严格按照PSP的各个流程进行撰写,整体完成度很好。- PSP中“计划共完成需要的时间”与“实际完成需要的时间”两列数据的差异化分析与原因探究:
实际完成需要的时间总是比计划共完成需要的时间要多,下次再制定计划共完成需要的时间可以进行适当的改进。
- 克隆结对方项目源码到本地机器,阅读并测试运行代码,参照《现代软件工程—构建之法》4.4.3节核查表复审同伴项目代码并记录
- 克隆结对方项目源码
![]()
- 测试运行代码
![]()
![]()
![]()
![]()
- 核查表复审
- 克隆结对方项目源码
| 核查表 | 执行情况 |
|---|---|
| 概要部分 | |
| 代码符合需求和规格说明么? | 代码基本符合需求 |
| 代码设计是否考虑周全? | 比较周全 |
| 代码可读性如何? | 可以顺利阅读 |
| 代码容易维护么? | 不太容易维护 |
| 代码的每一行都执行并检查过了吗? | 检查过了都可执行 |
| 设计规范部分 | |
| 设计是否遵从已知的设计模式或项目中常用的模式? | 基本遵从 |
| 代码有没有依赖于某一平台,是否会影响将来的移植(如Win32到Win64)? | 没有影响 |
| 开发者新写的代码能否用已有的Library/SDK/Framework中的功能实现? 在本项目中是否存在类似的功能可以调用而不用全部重新实现? |
能,存在 |
| 有没有无用的代码可以清除?(很多人想保留尽可能多的代码,因为以后可能会用上,这样导致程序文件中有很多注释掉的代码,这些代码都可以删除,因为源代码控制已经保存了原来的老代码) | 有 |
| 代码规范部分 | |
| 修改的部分符合代码标准和风格么? | 不符合 |
| 具体代码部分 | |
| 有没有对错误进行处理? 对于调用的外部函数,是否检查了返回值或处理了异常? |
进行了处理,检查了并处理了异常 |
| 参数传递有无错误,字符串的长度是字节的长度还是字符(可能是单/双字节)的长度,是以0开始计数还是以1开始计数? | 无错误;本项目中是以0开始计数。 |
| 边界条件是如何处理的? switch语句的default分支是如何处理的? 循环有没有可能出现死循环? |
switch语句的default分支返回false,没有出现死循环。 |
| 有没有使用断言(Assert)来保证我们认为不变的条件真的得到满足? | 没有 |
| 对资源的利用是在哪里申请,在哪里释放的? 有没有可能导致资源泄露(内存、文件、各种GUI资源、数据库访问的连接,等等)? 有没有优化的空间? |
在内存中完成,有可能泄露 |
| 数据结构中有没有用不到的元素? | 没有 |
| 效能 | |
| 代码的效能(Performance)如何? 最坏的情况如何? |
基本达到要求 |
| 代码中,特别是循环中是否有明显可优化的部分(C++中反复创建类,C#中 string 的操作是否能用StringBuilder 来优化)? | 有 |
| 对于系统和网络调用是否会超时? 如何处理? |
不会 |
| 可读性 | |
| 代码可读性如何? 有没有足够的注释? |
可顺利阅读,有足够的注释 |
| 可测试性 | |
| 代码是否需要更新或创建新的单元测试? 针对特定领域的开发(如数据库、网页、多线程等),可以整理专门的核查表 |
需要 |
- 依据复审结果尝试利用github的Fork、Clone、Push、Pull request、Merge pull request等操作对同伴个人项目仓库的源码进行合作修改。
- 任务三完成情况说明:
- PSP流程:
| PSP2.1 | 任务内容 | 计划完成需要的时间(min) | 实际完成需要的时间(min) |
|---|---|---|---|
| Planning | 计划 | 60 | 80 |
| Estimate | 估计这个任务需要多少时间,并规划大致工作步骤 | 70 | 85 |
| Development | 开发 | 2650 | 2850 |
| Analysis | 需求分析 (包括学习新技术) | 60 | 60 |
| Design Spec | 生成设计文档 | 50 | 60 |
| Design Review | 设计复审 (和同事审核设计文档) | 60 | 60 |
| Coding Standard | 代码规范 (为目前的开发制定合适的规范) | 40 | 50 |
| Design | 具体设计 | 80 | 85 |
| Coding | 具体编码 | 2000 | 2300 |
| Code Review | 代码复审 | 180 | 200 |
| Test | 测试(自我测试,修改代码,提交修改) | 150 | 160 |
| Reporting | 报告 | 200 | 210 |
| Test Report | 测试报告 | 60 | 60 |
| Size Measurement | 计算工作量 | 50 | 55 |
| Postmortem & Process Improvement Plan | 事后总结 ,并提出过程改进计划 | 120 | 150 |
- 需求分析:
- 平台基础功能:实验二中的任务3
- D{0-1}KP实例数据集存储到数据库
- 平台可动态嵌入任何一个有效的D{0-1}KP 实例求解算法,并保存算法实验日志数据
- 人机交互界面要求为GUI界面
- 设计遗传算法求解D{0-1}KP
- 软件设计说明:
- GUI界面:
- 前端界面:主要采用Springboot+layui
- 前端的GUI使用的是layui的框架,前端界面的显示是通过layui提供的模板,以及themeleaf、js等要素构成。
- themeleaf提供了强大的模板支持,本次实验中,themeleaf出演的角色是抽取公共的核心的DOM元素,在其它的前端页面通过调用的方式进行插入DOM节点,大大节约了开发的成本,提高了代码的可重用性;而layui主要是提供各种各样的优化的按钮、文本等之类的组件。
- layui是国人构建的一个前端框架,由于开发者是做后端的程序员,所以,layui提供的接口是与后端进行了无缝衔接,同时,它通过简单的定制,便可使得页面渲染的效果极佳。
- layui前端元素的显示是通过设置其class属性,达到显示元素的效果较为美观,通过layui封装的js,即可实现数据的异步传输(常见的网络通信有AJAX、axios、表单等,其中,前两项属于异步通信),它接收的服务器返回的参数必须是JSON格式,因此,它的js文件可能封装了AJAX,它要求后端返回的json数据必须是数组格式(key为data)、数据的长度(key为count)、数据的额外信息(key为msg)、数据成功与否(key为code),数据域(data为json对象或者hashmap)。layui的封装的js用于请求后台的数据,并显示在界面上(layui是通过模块化加载的,因此,需要引入响应的模块)。
- 前端界面:主要采用Springboot+layui
- 本次项目的前端需要引用的js文件是通过cdn去加载的,因此,项目的运行需要在网络允许的范围内才能使用。
- 后台功能:主要包括路由转发以及数据库的操作。
- 路由的实现:主要是通过controller进行处理和转发,只需要将路径写对即可。
- 数据的加载与显示:主要是通过从数据库中获取数据,构造json对象,返回到前端即可,需要注意的是,所有的服务器返回的数据必须是键值对的形式,最好是json(json只是键值对的一种,比如hashmap也是键值对的形式)
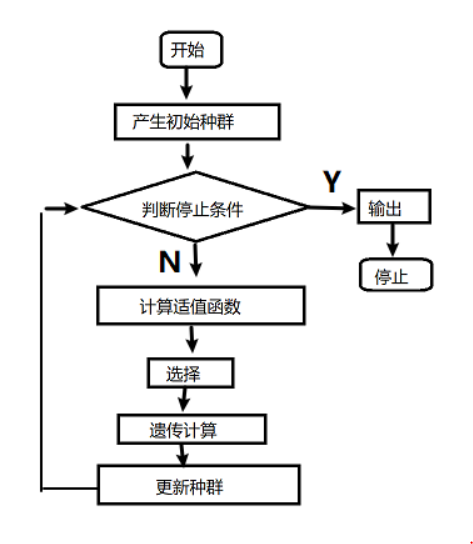
- 遗传算法:
- 算法介绍:是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。该算法通过数学的方式,利用计算机仿真运算,将问题的求解过程转换成类似生物进化中的染色体基因的交叉、变异等过程。是一种近似算法。
- 算法流程:
![]()
- 关键步骤如下:
(1)基因编码:在这个过程中,尝试对一些个体的基因做一个描述,构造这些基因的结构,有点像确定函数自变量的过程。
(2)设计初始群体:在这里需要造一个种群出来,这些种群有很多生物个体但基因不同。
(3)适应度计算:这里对那些不符合要求的后代进行剔除,不让他们产生后代。否则他们产生的后代只会让计算量更大而对逼近目标没有增益。
(4)产生下一代:有3种方法,即:直接选择,基因重组,基因突变
而后回到步骤(3)进行循环,适应度计算,产生下一代,这样一代一代找下去,直到找到最优解为止。
- GUI界面:
- 项目测试:
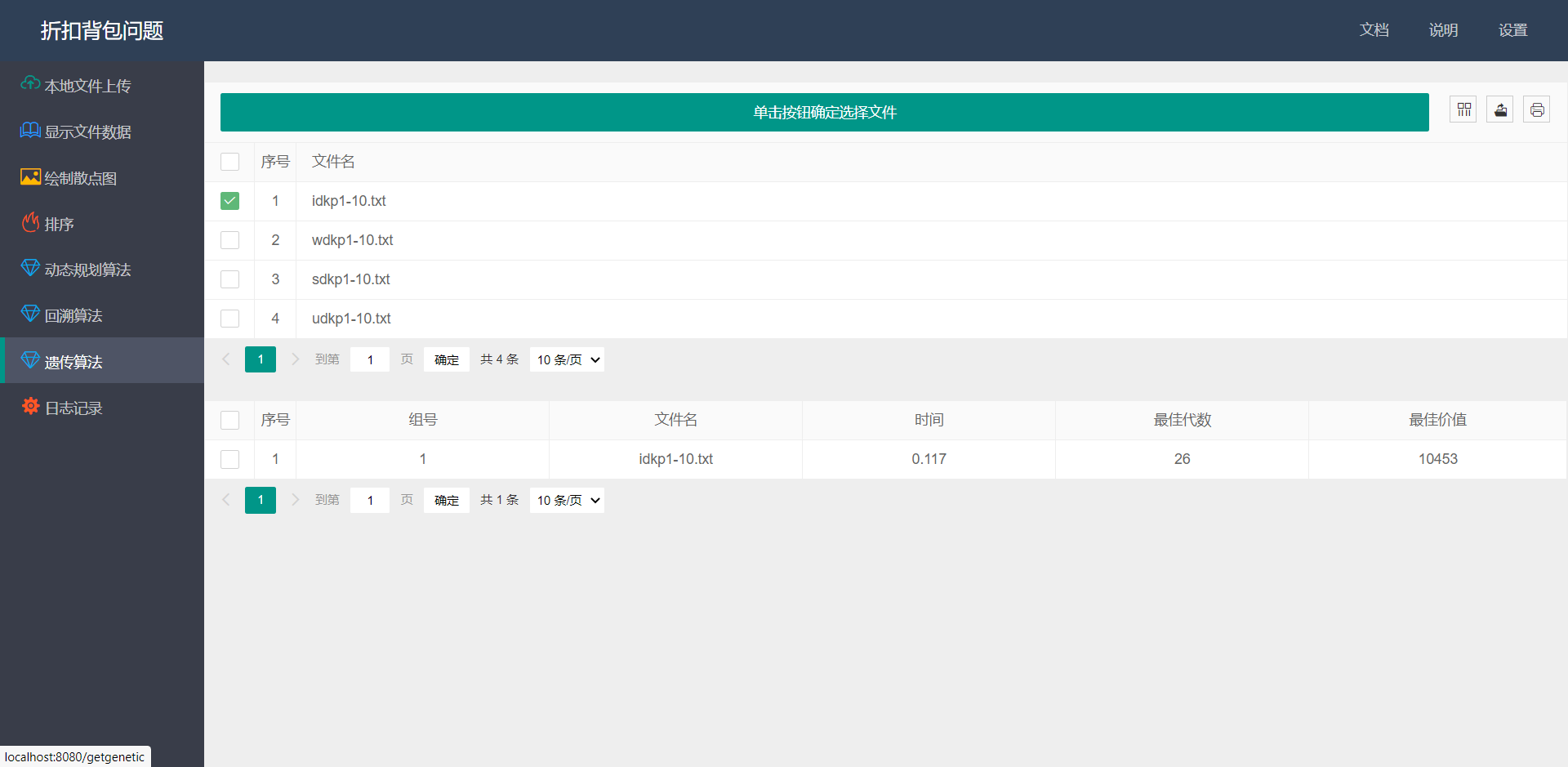
- GUI界面:
![]()
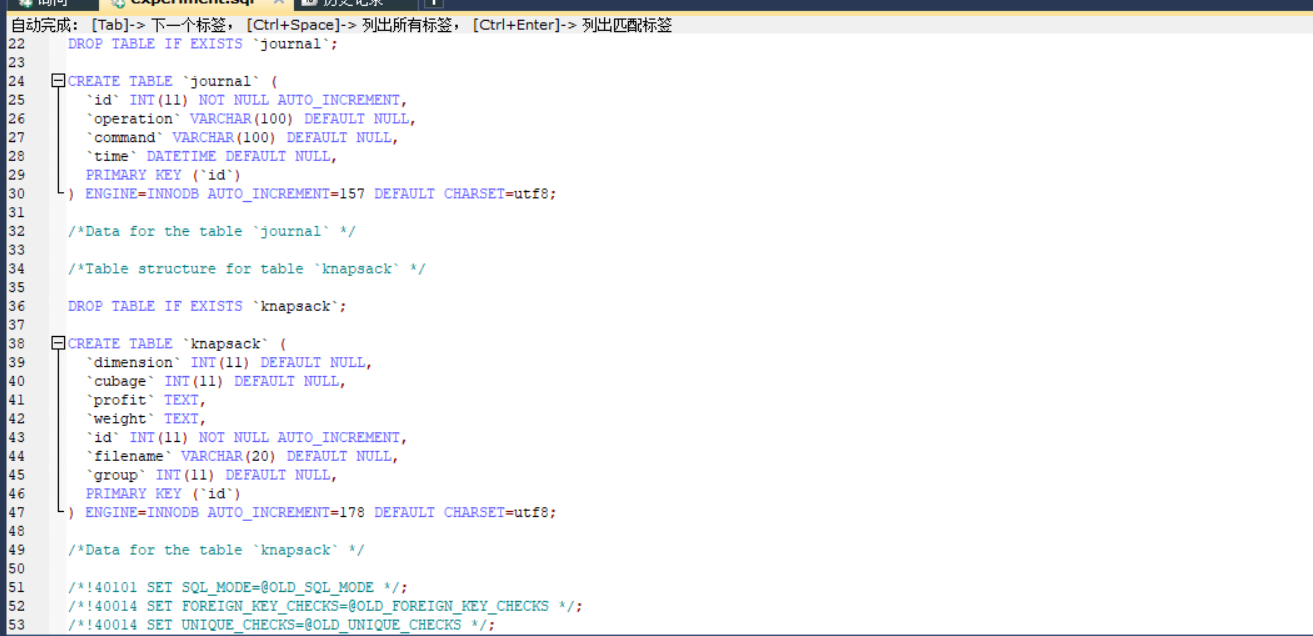
- 数据库:
- SQL语句:
![]()
- 基本表:
![]()
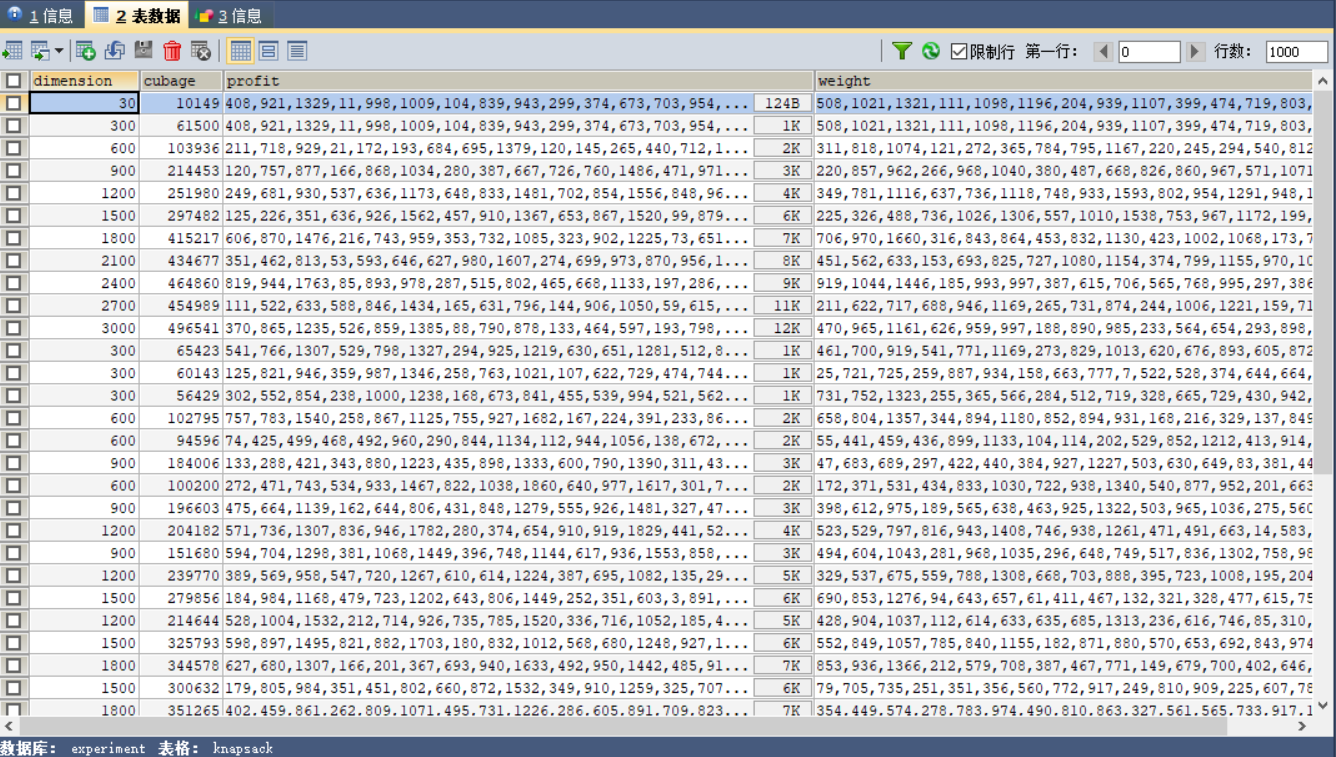
- 数据集有效信息:
![]()
- SQL语句:
- 实验二任务3的移植:
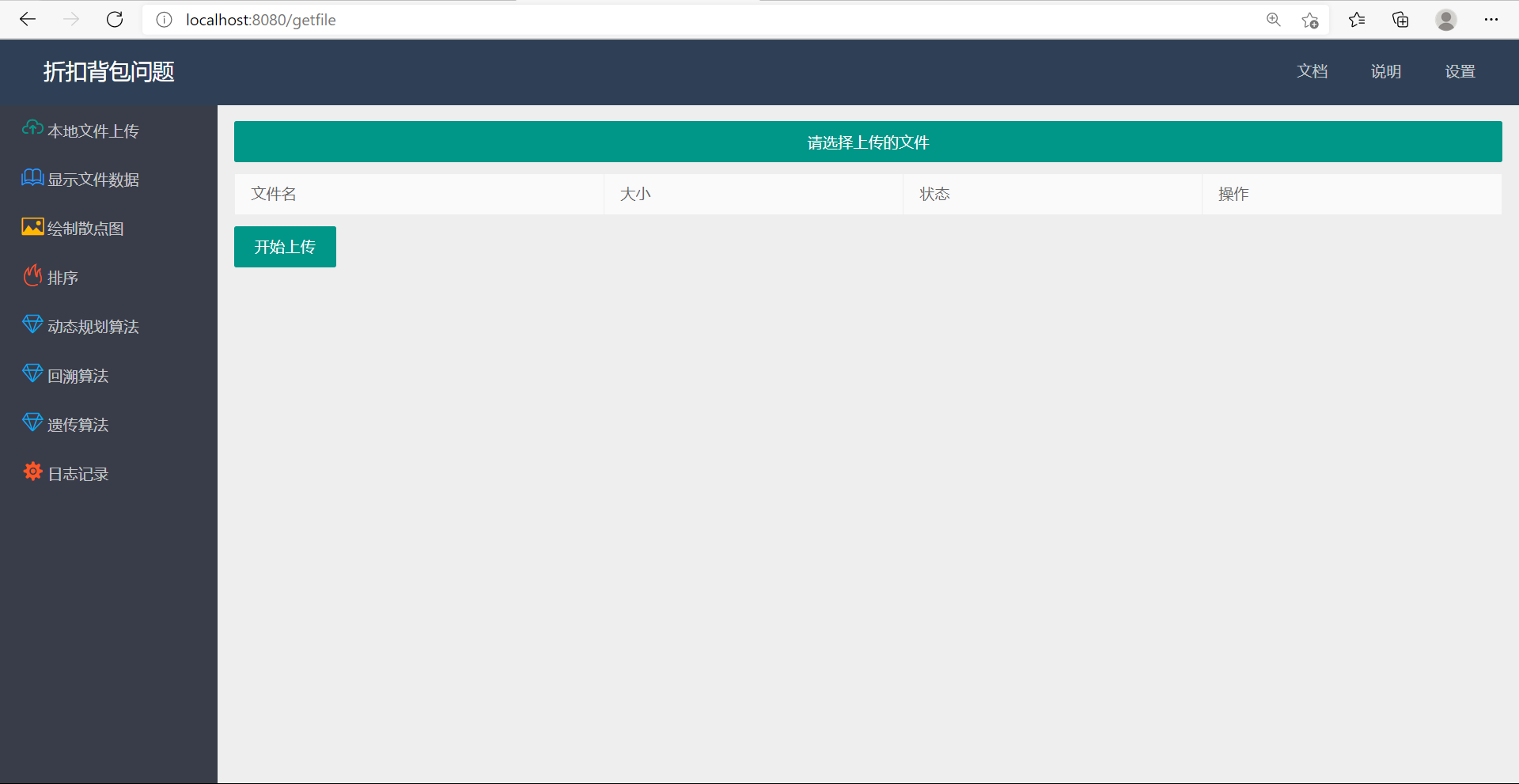
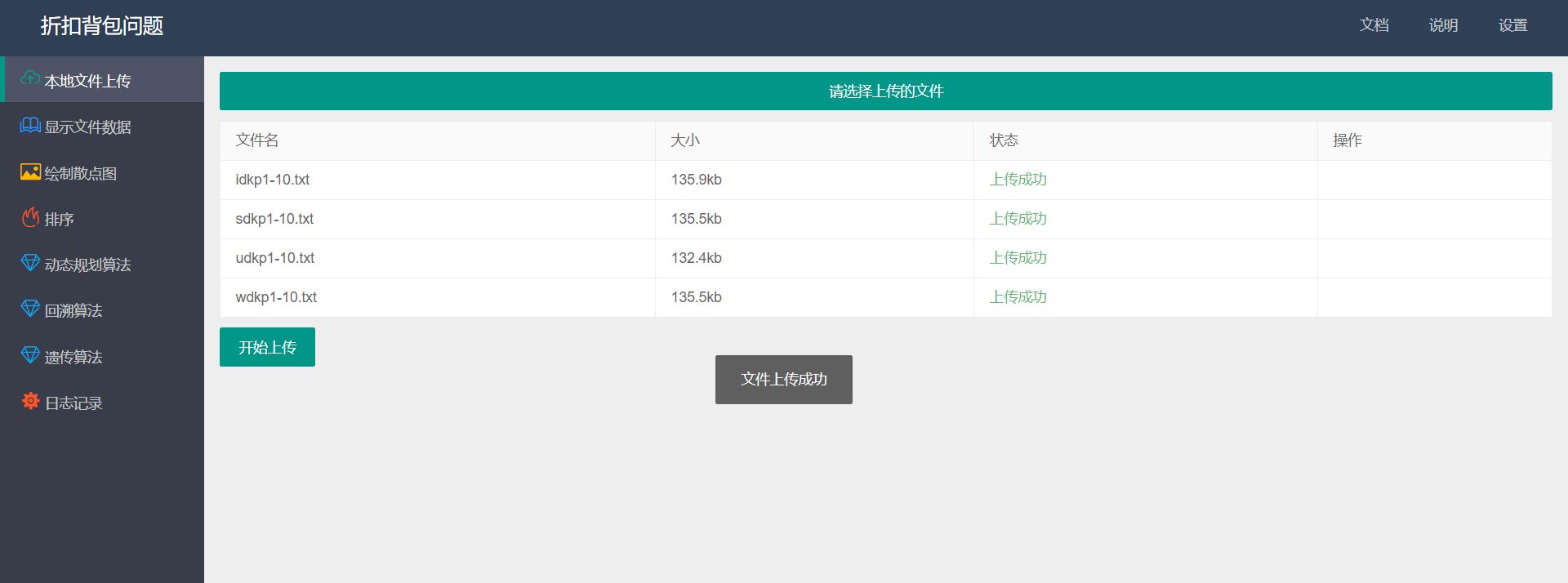
- 数据集的上传:
![]()
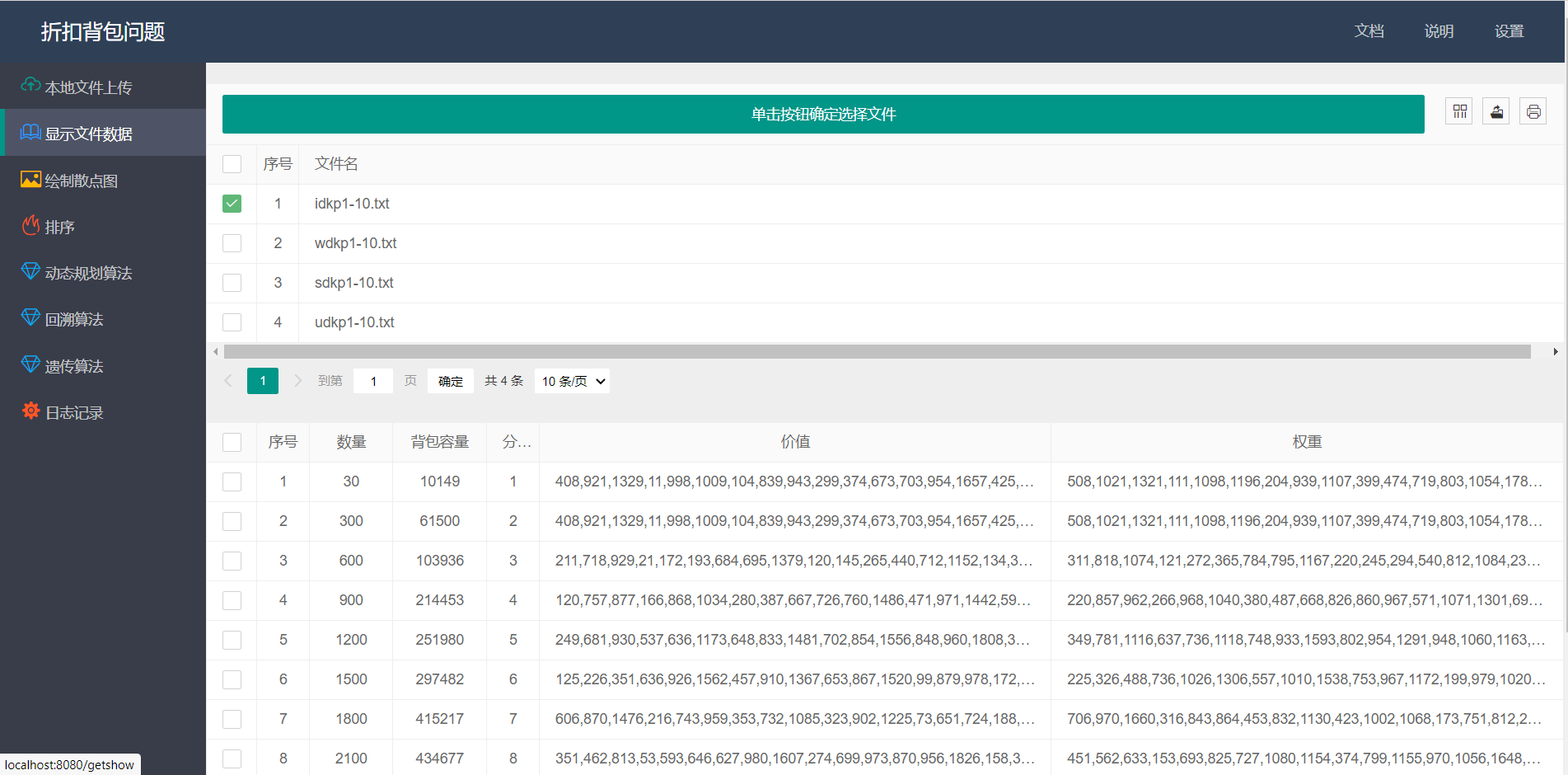
- 数据集的查看:
![]()
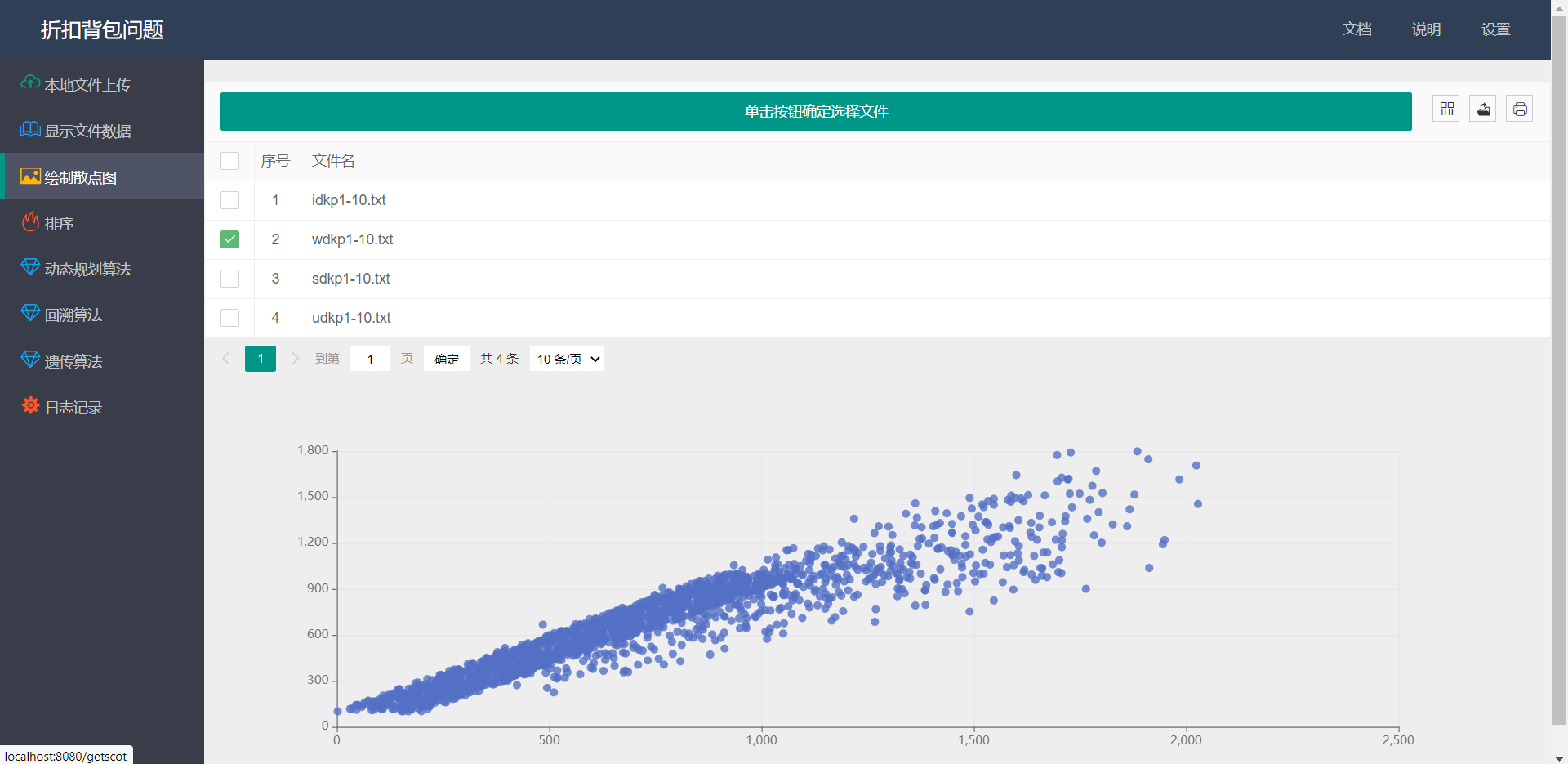
- 散点图:
![]()
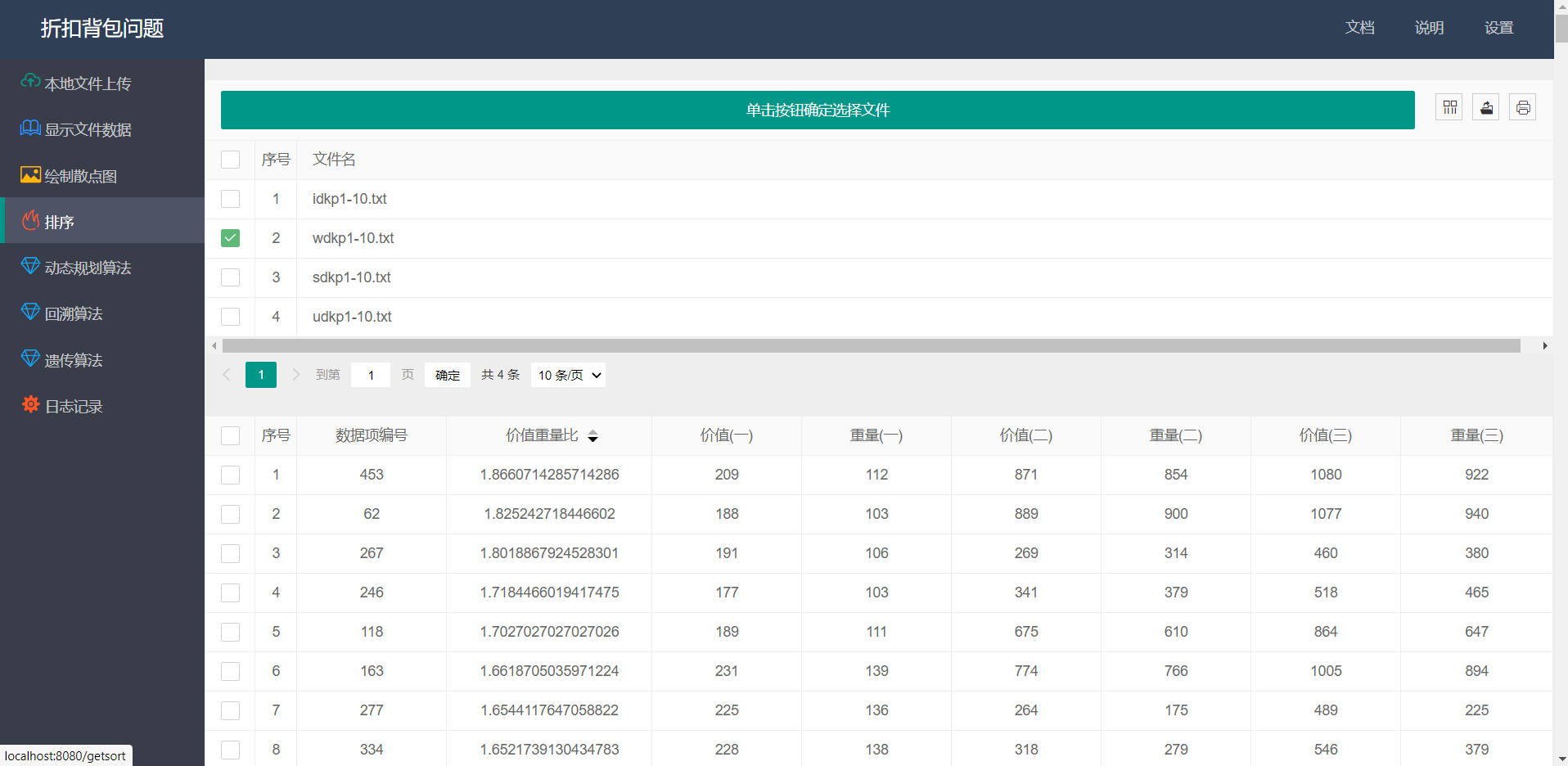
- 数据排序:
![]()
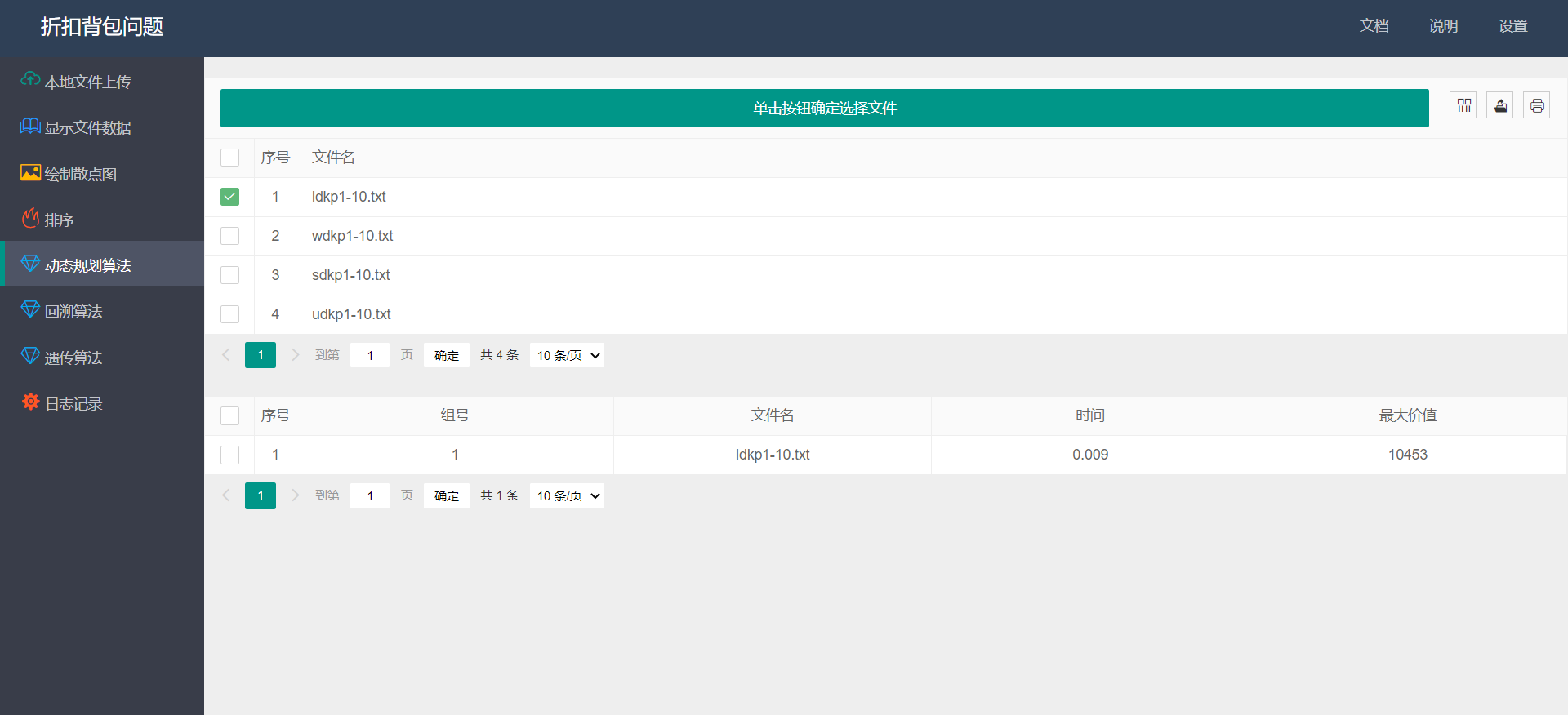
- 动态规划算法:
![]()
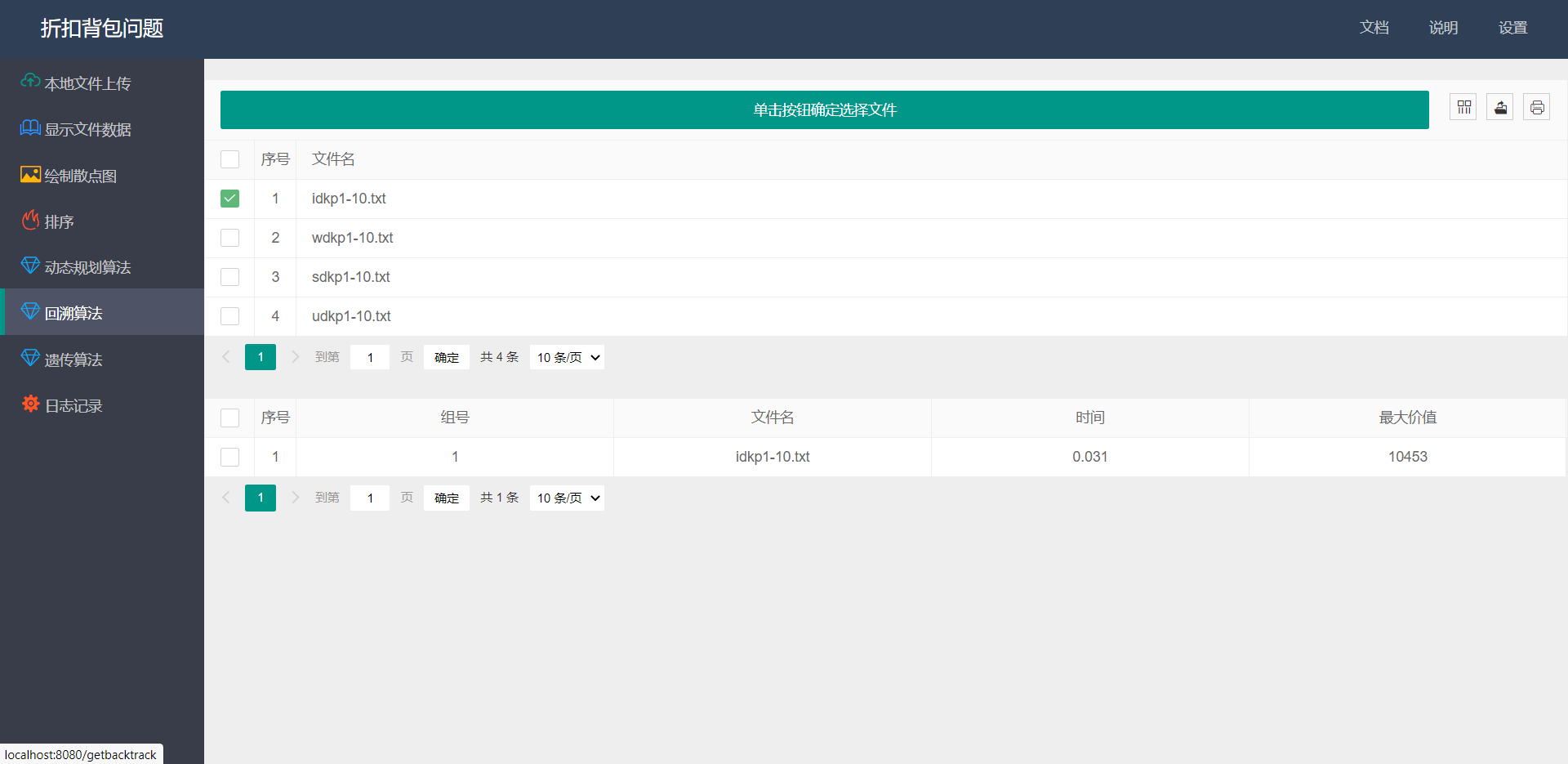
- 回溯算法:
![]()
- 数据集的上传:
- 遗传算法:
- 本地测试:
- 初始化种群:
![]()
- 迭代后的种群:
![]()
- 初始化种群:
- 本地测试:
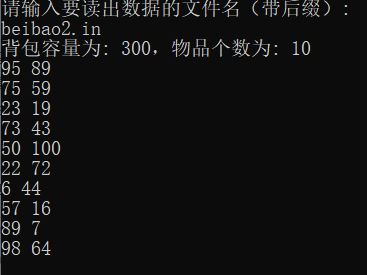
- 最优解求解(其中最佳编码为最优解,从前往后分别为各组数据,二分量中前一个表示1:选择该组数据,0:不选该组数据;后一个表示选择了该组数据的哪一个变量)
![]()
- 数据集:
![]()
- 数据集:
- 答案验证:
价值:1329+998+1657+1375+971+815+1360+1948=10453
重量:1321+1098+1781+1362+903+894+1241+1545=10145<10149 - "id-kp1-10.txt"数据集的第1组数据
![]()
动态规划计算出来的最优解为70106,误差值为791,误差值为1%,准确率可以接受。 - web测试:
![]()
- GUI界面:
- 软件实现及核心功能代码展示:
- 回溯算法:
private void dfs(int x){
back_count++;
if(back_count>INF){
res=-1;
return ;
}
if(x>=row) {
return ;
}
else {
if(weight[x+1][2]<=back_weight) {
back_weight-=weight[x+1][2];
back_value+=value[x+1][2];
if(res<back_value) {
res=back_value;
}
dfs(x+1);
back_weight+=weight[x+1][2];
back_value-=value[x+1][2];
}
dfs(x+1);
if(weight[x+1][0]<=back_weight) {
back_weight-=weight[x+1][0];
back_value+=value[x+1][0];
dfs(x+1);
if(res<back_value) {
res=back_value;
}
back_weight+=weight[x+1][0];
back_value-=value[x+1][0];
}
if(weight[x+1][1]<=back_weight) {
back_weight-=weight[x+1][1];
back_value+=value[x+1][1];
if(res<back_value) {
res=back_value;
}
dfs(x+1);
back_weight+=weight[x+1][1];
back_value-=value[x+1][1];
}
}
}
- 动态规划算法:
private Long knapSack(int[] weight, int[] profit, int C)
{
int n = profit.length/3;//profit一定是3的倍数
int[][] maxvalue = new int[n + 1][C + 1];//价值矩阵
long before=System.currentTimeMillis();
for (int i = 0; i < maxvalue.length; i++) {
maxvalue[i][0] = 0;
}
for (int i = 0; i < maxvalue[0].length; i++) {
maxvalue[0][i] = 0;
}
for (int i = 1; i < maxvalue.length; i++) {//不处理第一行
for (int j = 1; j <maxvalue[0].length; j++) {//不处理第一列
//处理每一个项集
int index=(i-1)*3;//计算当前的索引值,这里以项集为单位进行计算
ArrayList<Integer> item=new ArrayList<>();
if (j<weight[index]&&j<weight[index+1]&&j<weight[index+2])
{
maxvalue[i][j]=maxvalue[i-1][j];
continue;
}
if(j>=weight[index])
item.add(Math.max(maxvalue[i-1][j],profit[index]+maxvalue[i-1][j-weight[index]]));
if(j>=weight[index+1])
item.add(Math.max(maxvalue[i-1][j],profit[index+1]+maxvalue[i-1][j-weight[index+1]]));
if(j>=weight[index+2])
item.add(Math.max(maxvalue[i-1][j],profit[index+2]+maxvalue[i-1][j-weight[index+2]]));
item.sort((Integer o1, Integer o2)->{
if (o1>o2) return -1;
else if (o1==o2) return 0;
else return 1;
});
maxvalue[i][j]=item.get(0);
}
}
long after=System.currentTimeMillis();
this.setOptimalSolution(maxvalue[n][C]);
return (after-before);
}
遗传算法:
// 初始化种群
private void initGroup() {
int k, i;
for (k = 0; k < scale; k++)// 种群数
{
// 01编码
for (i = 0; i < LL; i++) {
oldPopulation[k][i] = random.nextInt(65535) % 2;
}
}
}
private best_one evaluate(int[] chromosome) {
// 010110
int vv = 0;
int bb = 0;
int str[]=new int[LL];
// 染色体,起始城市,城市1,城市2...城市n
for (int i = 0; i < LL; i++) {
if (chromosome[i] == 1) {
int temp=random.nextInt(65535) % 64;
if(temp<2) {
vv += v[i][temp];
bb += b[i][temp];
str[i] = temp + 1;
}
else{
vv += v[i][2];
bb += b[i][2];
str[i] = 3;
}
}
else {
str[i]=0;
}
}
if (bb > pb) {
// 超出背包体积
best_one x =new best_one();
x.x=0;x.y=str;
return x;
} else {
best_one x =new best_one();
x.x=vv;x.y=str;
return x;
}
}
// 计算种群中各个个体的累积概率,前提是已经计算出各个个体的适应度fitness[max],作为赌轮选择策略一部分,Pi[max]
private void countRate() {
int k;
double sumFitness = 0;// 适应度总和
int[] tempf = new int[scale];
for (k = 0; k < scale; k++) {
tempf[k] = fitness[k];
sumFitness += tempf[k];
}
Pi[0] = (float) (tempf[0] / sumFitness);
for (k = 1; k < scale; k++) {
Pi[k] = (float) (tempf[k] / sumFitness + Pi[k - 1]);
}
}
// 挑选某代种群中适应度最高的个体,直接复制到子代中
// 前提是已经计算出各个个体的适应度Fitness[max]
private void selectBestGh() {
int k, i, maxid;
int maxevaluation;
int max_str[] = null;
maxid = 0;
maxevaluation = fitness[0];
for (k = 1; k < scale; k++) {
if (maxevaluation < fitness[k]) {
maxevaluation = fitness[k];
max_str=fitness_str[k];
maxid = k;
}
}
if (bestLength < maxevaluation) {
bestLength = maxevaluation;
best_str=max_str;
bestT = t;// 最好的染色体出现的代数;
for (i = 0; i < LL; i++) {
bestTour[i] = oldPopulation[maxid][i];
}
}
// 复制染色体,k表示新染色体在种群中的位置,kk表示旧的染色体在种群中的位置
copyGh(0, maxid);// 将当代种群中适应度最高的染色体k复制到新种群中,排在第一位0
}
// 赌轮选择策略挑选
private void select() {
int k, i, selectId;
float ran1;
for (k = 1; k < scale; k++) {
ran1 = (float) (random.nextInt(65535) % 1000 / 1000.0);
// System.out.println("概率"+ran1);
// 产生方式
for (i = 0; i < scale; i++) {
if (ran1 <= Pi[i]) {
break;
}
}
selectId = i;
copyGh(k, selectId);
}
}
private void evolution() {
int k;
// 挑选某代种群中适应度最高的个体
selectBestGh();
// 赌轮选择策略挑选scale-1个下一代个体
select();
float r;
// 交叉方法
for (k = 0; k < scale; k = k + 2) {
r = random.nextFloat();// /产生概率
// System.out.println("交叉率..." + r);
if (r < Pc) {
// System.out.println(k + "与" + k + 1 + "进行交叉...");
OXCross(k, k + 1);// 进行交叉
} else {
r = random.nextFloat();// /产生概率
// System.out.println("变异率1..." + r);
// 变异
if (r < Pm) {
// System.out.println(k + "变异...");
OnCVariation(k);
}
r = random.nextFloat();// /产生概率
// System.out.println("变异率2..." + r);
// 变异
if (r < Pm) {
// System.out.println(k + 1 + "变异...");
OnCVariation(k + 1);
}
}
}
}
// 两点交叉算子
private void OXCross(int k1, int k2) {
int i, j, flag;
int ran1, ran2, temp = 0;
ran1 = random.nextInt(65535) % LL;
ran2 = random.nextInt(65535) % LL;
while (ran1 == ran2) {
ran2 = random.nextInt(65535) % LL;
}
if (ran1 > ran2)// 确保ran1<ran2
{
temp = ran1;
ran1 = ran2;
ran2 = temp;
}
flag = ran2 - ran1 + 1;// 个数
for (i = 0, j = ran1; i < flag; i++, j++) {
temp = newPopulation[k1][j];
newPopulation[k1][j] = newPopulation[k2][j];
newPopulation[k2][j] = temp;
}
}
// 多次对换变异算子
private void OnCVariation(int k) {
int ran1, ran2, temp;
int count;// 对换次数
count = random.nextInt(65535) % LL;
for (int i = 0; i < count; i++) {
ran1 = random.nextInt(65535) % LL;
ran2 = random.nextInt(65535) % LL;
while (ran1 == ran2) {
ran2 = random.nextInt(65535) % LL;
}
temp = newPopulation[k][ran1];
newPopulation[k][ran1] = newPopulation[k][ran2];
newPopulation[k][ran2] = temp;
}
}
private void solve() {
int i;
int k;
// 初始化种群
initGroup();
// 计算初始化种群适应度,Fitness[max]
for (k = 0; k < scale; k++) {
best_one temp= evaluate(oldPopulation[k]);
fitness[k]=temp.x;
fitness_str[k]=temp.y;
}
// 计算初始化种群中各个个体的累积概率,Pi[max]
countRate();
for (t = 0; t < MAX_GEN; t++) {
evolution();
// 将新种群newGroup复制到旧种群oldGroup中,准备下一代进化
for (k = 0; k < scale; k++) {
for (i = 0; i < LL; i++) {
oldPopulation[k][i] = newPopulation[k][i];
}
}
// 计算种群适应度
for (k = 0; k < scale; k++) {
best_one temp= evaluate(oldPopulation[k]);
fitness[k]=temp.x;
fitness_str[k]=temp.y;
}
// 计算种群中各个个体的累积概率
countRate();
}
}
- 文件读取存储模块:
public boolean getAllParameterByFile(String filePath) throws IOException {
//若目录不存在,则创建目录
File file=new File(filePath);
String data= FileUtils.readFileToString(file,"UTF-8");
//初步格式化件
String getTextByDeleteWhiteSpace=StringUtils.deleteWhitespace(data);//删除所有的空格
if (getTextByDeleteWhiteSpace.charAt(2)=='*') {
int getFirstDKPIndex = getTextByDeleteWhiteSpace.indexOf("DKP");//获得首次出现DKP的位置
String formatPrefixText = getTextByDeleteWhiteSpace.substring(getFirstDKPIndex + 3);//删除冒号以前的字符
int getLastFullIndex = formatPrefixText.lastIndexOf('.');//获得最后一次出现.的位置
int getLastCommaIndex = formatPrefixText.lastIndexOf(',');//获得最后一次出现,的位置
int index = getLastFullIndex > getLastCommaIndex ? getLastFullIndex : getLastCommaIndex;//获得格式化后的文本
String formatSuffixText = formatPrefixText.substring(0, index);
getProfitAndWeight(formatSuffixText);//获取profit和weight
return true;
}else{
return false;
}
}
- 结对过程:
![]()
- 总结:
在组员积极交流且按照极限编程的方式进行项目开发是可以带来1+1>2的效果。结对编程要特别注意代码的规范问题,以及数组的下标。结对编程时要多保持交流,积极反馈当前遇到的问题与解决措施。但如果两个人在一起工作时,其中一个人想偷懒去干别的,那么就会拖延工作进度。两人互相监督工作,可以增强代码和产品质量,并有效的减少BUG。在编程中,相互讨论,可以更快更有效地解决问题,互相请教对方,可以得到能力上的互补。由于时间紧张,web界面还没有将解向量的数据输出到前端界面。





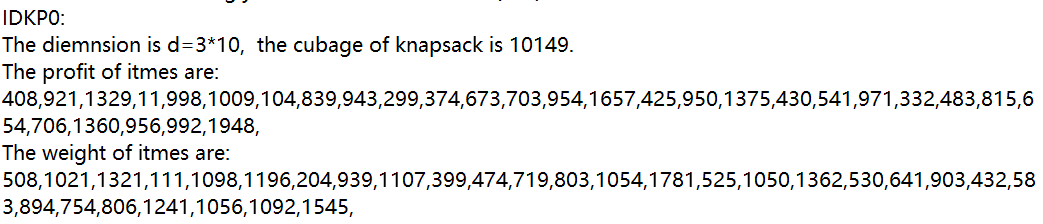


 浙公网安备 33010602011771号
浙公网安备 33010602011771号