20172305 2017-2018-2 《程序设计与数据结构》实验三报告
20172305 2017-2018-2 《程序设计与数据结构》实验三报告
课程:《程序设计与数据结构》
班级: 1723
姓名: 谭鑫
学号:20172305
实验教师:王志强
实验日期:2018年11月21日
必修/选修: 必修
1.实验内容
-
实验三-1-查找和排序:
- (1)定义一个Searching和Sorting类,并在类中实现linearSearch(教材P162 ),SelectionSort方法(P169),最后完成测试。
- (2)要求不少于10个测试用例,提交JUnit测试用例设计情况(正常,异常,边界,正序,逆序),用例数据中要包含自己学号的后四位
-
实验三-2-查找和排序:
- (1)重构你的代码把Sorting.java Searching.java放入cn.edu.besti.cs1723.(姓名首字母+四位学号)包中(例如:cn.edu.besti.cs1723.G2301)把测试代码放test包中重新编译,运行代码,提交编译,运行的截图(IDEA,命令行两种)
-
实验三-3-查找和排序:
- (1)参考 在Searching中补充查找算法并测试
-
实验三-4-查找和排序:
- (1)补充实现课上讲过的排序方法:希尔排序,堆排序,二叉树排序等(至少3个)测试实现的算法(正常,异常,边界)提交运行结果截图
-
实验三-5-查找和排序(选做):
- (1)编写Android程序对各种查找与排序算法进行测试
2. 实验过程及结果
-
实验三-1-查找和排序:测试选择排序和顺序查找两个方法,其实很简单,相关代码之前都写过或是书上都有,但是要用到JUnit测试,正常写个驱动类就好,但是非要用到JUnit测试,只能找回娄老师的博客和自己上学期的实验二博狂补。
- 排序的测试:

- 查找的测试:
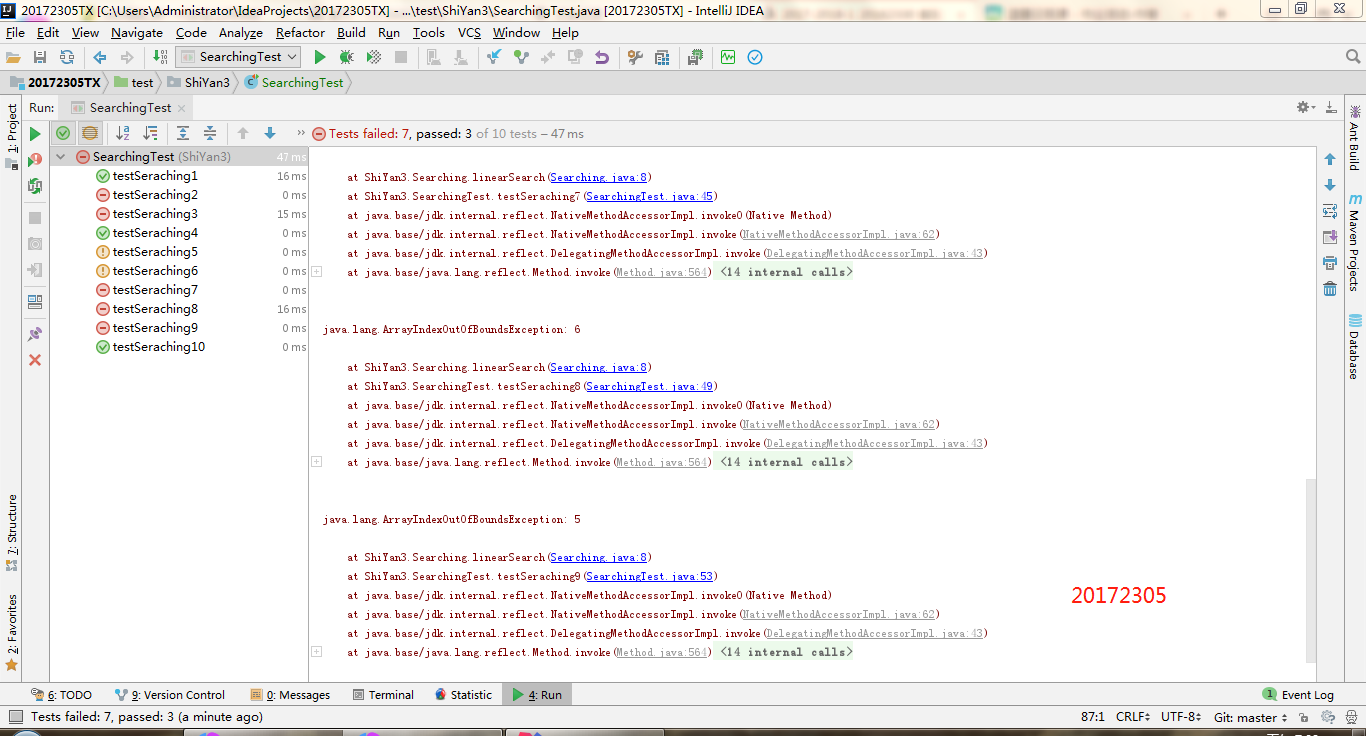
- 排序的测试:
-
实验三-2-查找和排序:将已有的类移动到一个新的包内实现代码的重构,简单的创建移动就好,但是需要在命令行下完成。瞬间炸裂,好在自己在实验室一直用的是Linux系统进行编译还是很简单的。但是,包名很长,在创建的时候总会是爆红,好在只是提醒,不然实验做不成了。在虚拟机创建的过程很简单,但是在运行的时候总会有问题,非安全操作...同样的代码在IDEA上就可以运行的,放到虚拟机里面就会有问题,很神奇。在校对了好几遍代码才发现有一行声明包名的代码,删掉就好。尝试在虚拟机上进行JUnit测试,发现代码不能正常运行就改为正常的编写驱动类进行测试。
- 包名的提示:
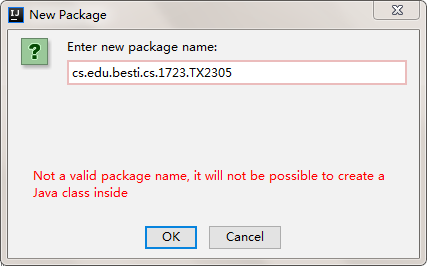
命令行操作:
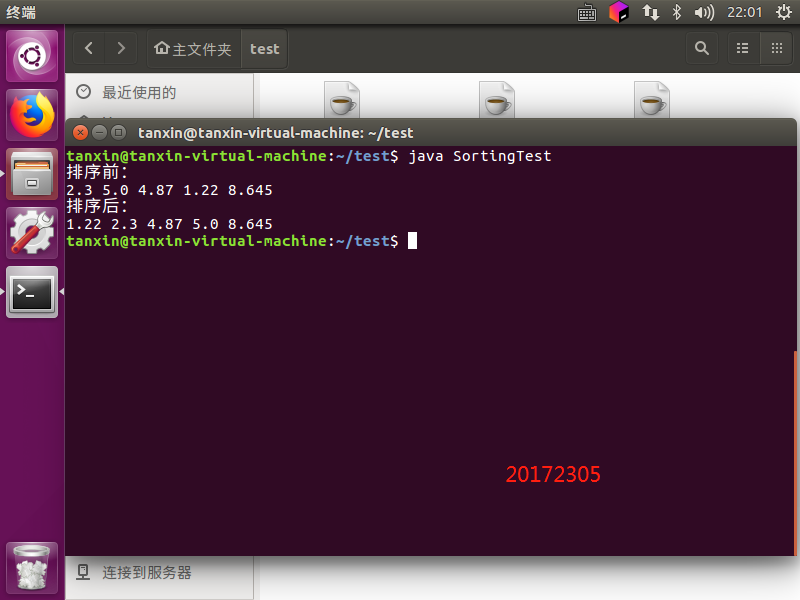
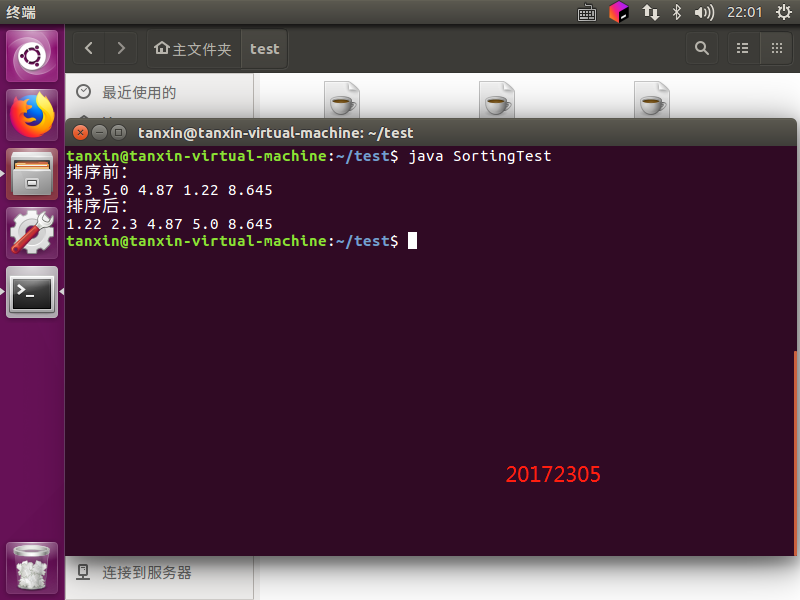
- 包名的提示:
-
实验三-3-查找和排序:根据博客上的查找方法在Searching内进行补充去其他查找方法,斐波那契查找(不是一个斐波那契数列么?)、二叉树查找、分块查找、哈希查找等。好在有博客支持,通过网上的资源实现了相关代码(具体代码会在问题中进行分析),在做这个实验的时候,始终在二分查找出有问题,一直没有解决,后来突然发现是二分查找要求是排序后的数组,而不是像顺序查找一样可以随便查找,还是知识记得不牢固,导致在这种问题上卡壳。

-
实验三-4-查找和排序:在Sorting中补充希尔排序,堆排序,二叉树排序等方法。堆排序是在堆部分实现的,二叉树排序就是用个AVL树就可以,不断比较添加元素的大小形成AVL树,最后可以在AVL树进行中序输出就可以,希尔排序也是之前做过的直接进行整合就可以。

-
实验三-5-查找和排序:(选做):在ANdroid实现相关代码的运行。
- 主界面(有点low...)
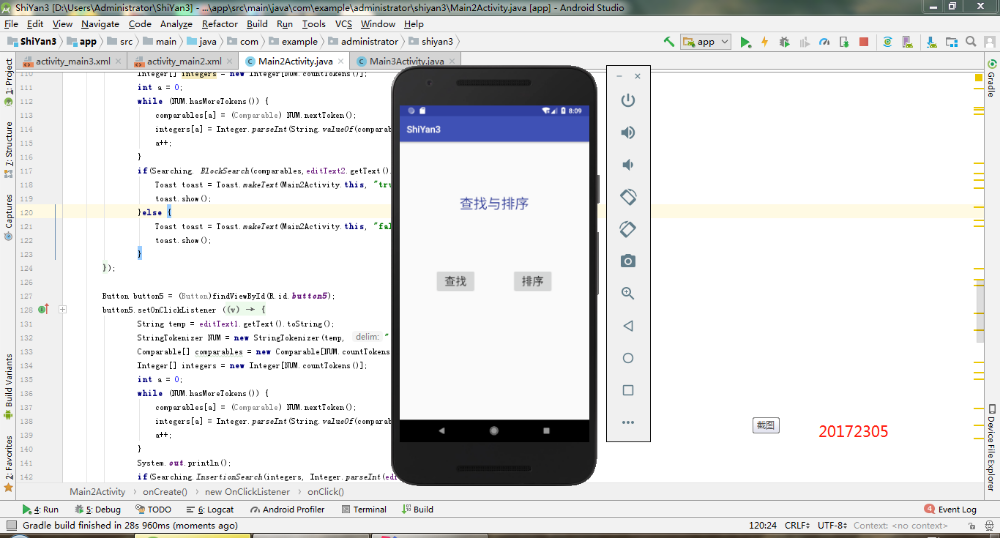
- 查找界面:
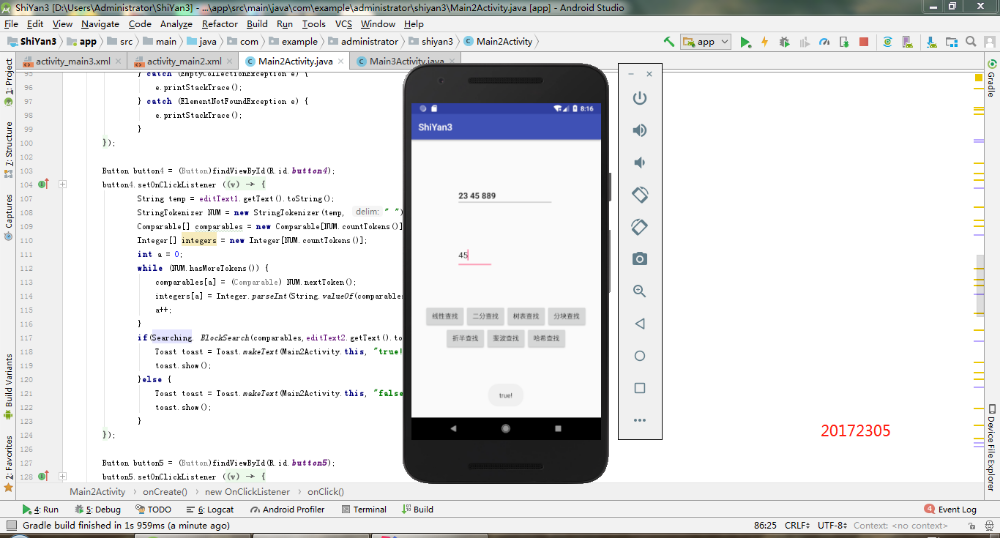
- 排序界面:
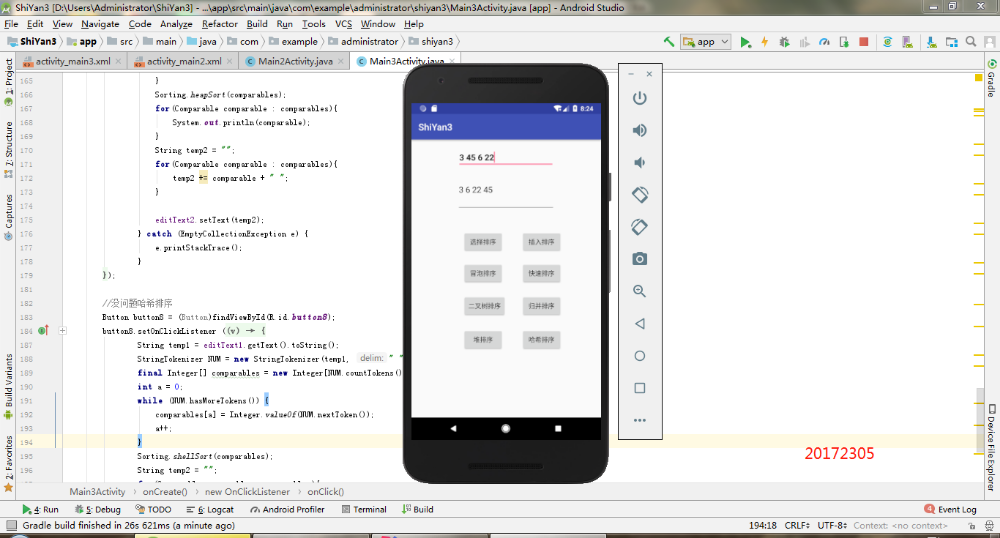
- 主界面(有点low...)
-
所有代码:
3. 实验过程中遇到的问题和解决过程
-
问题1:针对老师给出的测试情况,我对边界情况和异常情况进行的疑惑?如何测试边界情况,是确定边界正确还是边界错误?以异常情况是指什么类型的异常?可以出现在创建数组、也可以在某些查找之前未进行排序、还是查无此物?
-
问题1的解决方案:感觉都可以,我的猜想都满合理的。所以,针对边界情况我尝试了在缩短边界范围查找超出边界的元素和范围内的元素,针对异常情况我尝试查找未存在的元素以及未进行排序就进行的查找,但是我觉得创建数组时的错误不应该算在方法的测试,应该算在编写过程出现的错误。
-
问题2:斐波那契查找?
-
问题2的解决方案:斐波那契是二分法的改进版,和折半查找类似。不同的是它利用了数学领域的黄金分割法则(也就是0.618法则),避免了死板的二分法则。
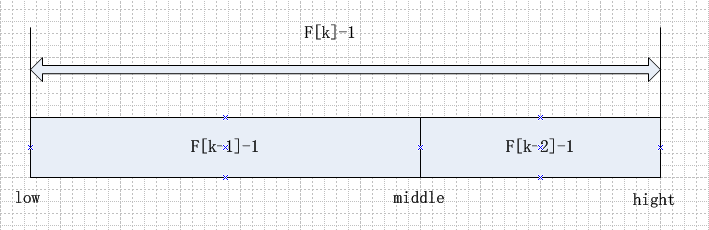
- 斐波那契查找的核心是:
- 1.0当k=a[mid]时,查找成功;
- 2.当k<F[mid]时,新的查找范围是第low个到第mid-1个,此时范围个数为F[k-1] - 1个,即数组左边的长度,所以要在[low, F[k - 1] - 1]范围内查找;
- 3.当k>a[mid]时,新的查找范围是第mid+1个到第high个,此时范围个数为F[k-2] - 1个,即数组右边的长度,所以要在[F[k - 2] - 1]范围内查找。
while (low <= high) { // low:起始位置 // 前半部分有fibonacci[temp1 - 1]个元素(斐波那契数组【temp1 - 1】),由于索引值从0开始 // 则-1 获取 黄金分割位置元素的索引值 mid = low + fibonacci[temp1 - 1] - 1; if (temp[mid] > (int)target) { // 查找前半部分,指针移动 high = mid - 1; // (全部元素) = (前半部分)+(后半部分) // fibonacci[temp1] = fibonacci[temp1 - 1] + fibonacci[temp1 - 1] // 因为前半部分有fibonacci[temp1 - 1]个元素,所以 k = k-1 temp1 = temp1 - 1; } else if (temp[mid] < (int)target) { // 查找后半部分,指针移动 low = mid + 1; // (全部元素) = (前半部分)+(后半部分) // fibonacci[temp1] = fibonacci[temp1 - 1] + fibonacci[temp1 - 1] // 因为后半部分有fibonacci[temp1 - 1]个元素,所以 temp1 = temp1 - 2 temp1 = temp1 - 2; } else { // 如果为真则找到相应的位置 if (mid <= high) { return mid + 1; } else { // 出现这种情况是查找到补充的元素 // 而补充的元素与high位置的元素一样 return high + 1; } } }
其他
实验三不像实验二那么复杂,就是一个整合排序和查找的实现,也同时温习了命令行运行的模式和JUnit测试。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号