Float和double丢失精度问题及解决方案

出现这种结果的原因：float和double类型尤其不适合用于货币运算，因为要让一个float或double精确的表示0.1或者任何其他负数次方值是不可能的（十进制系统中不能准确的表示出1/3，同样二进制系统也不能准确的表示1/10）。

1.十进制整数转为二进制数：

例子：11表示成二进制数：

11/2 =5 余1

5/2 = 2 余1

2/2 = 1 余0

1/2 = 0 余1

0结束，11二进制表示为(从下往上):1011

注意：只要遇到除以后的结果为0就结束了。所有的整数除以2一定能够最终得到0，但是小数就不能，小数转变为二进制的算法就有可能会无限循环下去。

2.十进制小数转为二进制数

算法是乘以2知道没有了小数为止，例子：

0.9表示成二进制数：

0.9*2 = 1.8 取整数部分：1

0.8*2 = 1.6 取整数部分：1

0.6*2 = 1.2 取整数：1

0.2*2 = 0.4 取整数：0

0.4*2 = 0.8 取整数：0

0.8*2 = 1.6 取整数：1

。。。。

0.9二进制表示为（从上往下）：1100100100100.......

注意：上面的计算过程循环了，也就是说乘以2永远不能消灭小数部分，这样算法将无限下去。显然，小数的二进制表示有时是不能精确的。道理很简单，十进制系统中不能准确的表示出1/3，同样二进制也无法准确的表示1/10。这也是浮点型出现精度丢失问题的主要原因。

解决方案一：

如果不介意记录十进制的小数点，而且数值不大，那么可以使用long,int等基本类型，

int resultInt = 10 -9;

double result  = (double)resultInt / 100;//自己控制小数点

解决方案二：

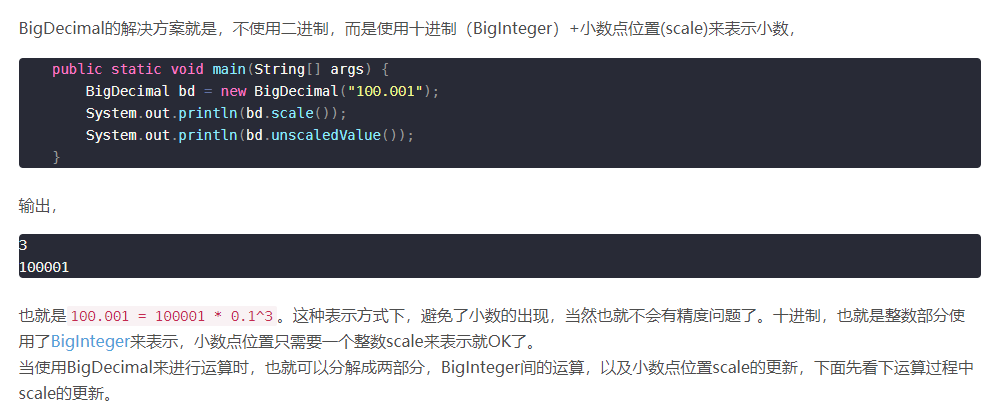
使用BigDecimal，而且需要在构造参数使用String类型.

float和double只能用来做科学计算或者工程计算，在商业计算等精确计算中，要用java.math.BigDecimal。

在《EffectiveJava》这本书中就给出了一个解决方法。该书中也指出，float和double只能用来做科学计算或者是工程计算，在商业计算等精确计算中，我们要用java.math.BigDecimal。

BigDecimal类一个有4个方法，我们只关心对我们解决浮点型数据进行精确计算有用的方法，即

BigDecimal(double value) // 将double型数据转换成BigDecimal型数据

原理：