神经影像中的坐标系统
一个MRI影像数据可以简化为一个多维数组加上元数据构成的集合。其中，元数据通常为影像数据的头信息。以结构影像为例，它由一个三维数组data和相应的元数据构成。
以下内容参考自[1]。
体素坐标
我们可以通过数组的下标来获取数组中任意位置元素的数值。这些下标即位数据的体素坐标。对于结构数据而言，它的体素坐标为三元组 (i, j, k)，相应位置上的值为 data[i, j, k]。
机器坐标
然而单通过体素坐标我们是无法知道影像在物理世界中的位置的。这里就引出了机器坐标。机器坐标通常以扫描仪的磁场中心为坐标原点，单位为毫米。假设有一个观察者站在扫描仪后面，面对着床尾。靠近观察者的方向为正方向。此坐标轴定义为scanner bore axis。定义穿过磁场中心，垂直于bore axis，方向为从屋顶到地板的轴为scanner-floor/ceiling axis。朝向屋顶为正方向。定义穿过磁场中心，垂直于bore axis，方向从观察者左边到右边的轴为scanner-left/right。正方向定义为向右。
在规定轴的顺序为(scanner left/right, scanner floor/ceiling, scanner bore)后，物理世界(x, y, z)=(10, -3, 5)就表示一个位于磁场中心相对于观察者向右10mm，向下3mm，靠近观察者方向距离5mm的点。
受试坐标
但是对于影像数据，我们通常需要知道上面每一个位置相对于受试的位置。由于受试在扫描仪里面并不一定是标准姿势，也就是平躺在扫描床上，头靠近扫描仪。因此在实际使用当中还需要考虑相对于受试者的坐标系统。再兼顾扫描仪的机器坐标的情况下，定义了机器-受试坐标。坐标原点还是机器的磁场中心，坐标轴的方向则是以受试者为标准。定义第一条轴为受试者左-右，向右为正；第二条轴为前-后，向前为正；第三条轴为上-下，向上为正。也记为RAS+。当受试处于标准姿势进行扫描时，三条轴分别对应机器坐标中的scanner-left/right, scanner-floor/ceiling和scanner bore。
通过头信息中的affine矩阵可以将体素坐标转换到相应的参照空间中。如下所示：
其中，\(m\)表示坐标的缩放和旋转，\(a, b, c\)表示在各自方向上的平移的距离。
其他坐标
有时候我们只是想知道影像中的某一点相对于标准空间中图像的位置。此时需要用到标准空间参考。有两种，MNI标准空间和Talairach标准空间。两者的差异在于坐标原点的位置不同。
Neurological和Radiological视图
Neurological视图可以理解为站在一个人的后面去观察他的大脑，因此观察者看到的左右就是受试实际的左右。而Radiological视图是观察一个面对着观察者的受试的大脑，观察者看到的左右与受试实际的左右是相反的。具体以下图为例。
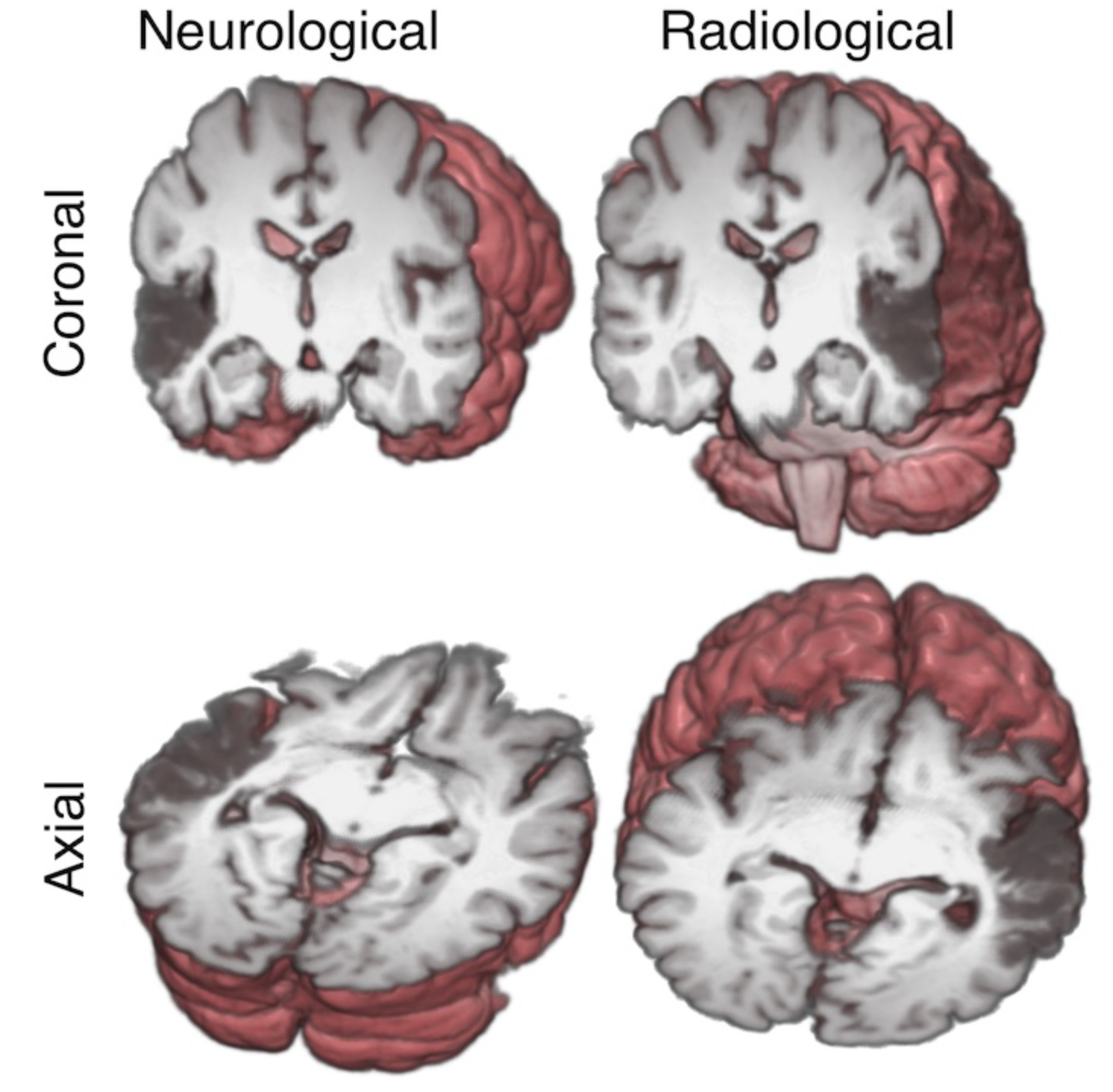
图1. Neurological和Radiological视图差异[2]。
