作图-线性坐标与对数坐标
线性坐标在显示有较大区值范围的\(x\)和\(y\)时（\(x\)和\(y\)的取值范围有很大尺度的差异）不能很清楚地将两者的对应关系表现出来。对于函数\(y=log_{10}x, x\in[1, 100000]\)在线性坐标下如图一所示。
import matplotlib.pyplot as plt
import numpy as np
x = np.arange(1, 100000)
y = np.log10(x)
plt.plot(
x,
y,
color='k',
lw=2)
plt.title('Linear')
plt.xlabel('x')
plt.ylabel('log(x)')
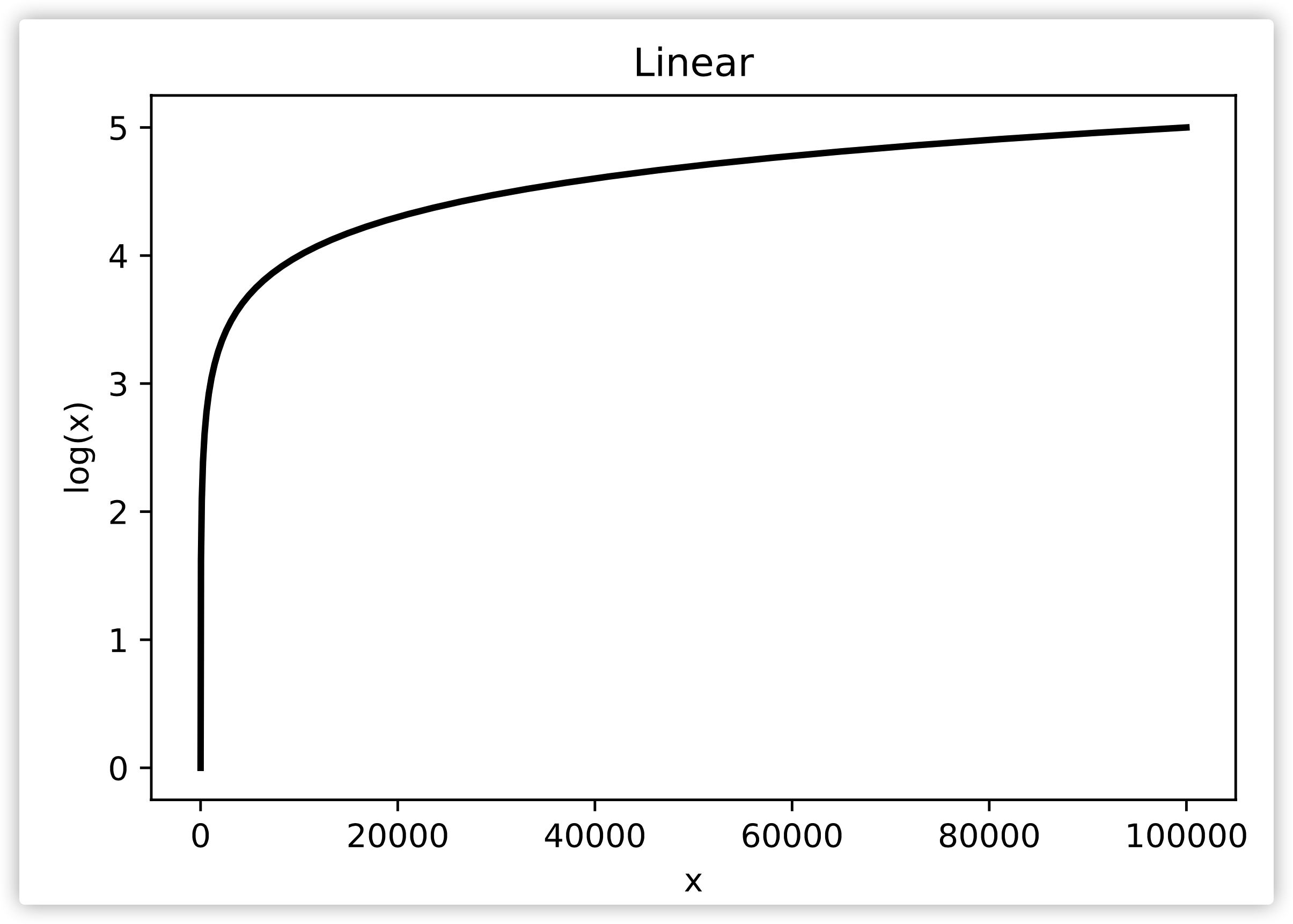
图一，对数函数在线性坐标下的图像。
很显然，对于\(x<1000\)对应的\(y\)是无法通过图来很清楚地确定的。通过对\(x\)进行对数转换则可以更加清楚地表示出\(x\)与\(y\)的关系。图二即为上述公式在对数坐标下的图形。
import matplotlib.pyplot as plt
import numpy as np
x = np.arange(1, 100000)
y = np.log10(x)
plt.plot(
x,
y,
color='k',
lw=2)
plt.title('x-log')
plt.xlabel('x')
plt.ylabel('log(x)')
plt.xscale('log')
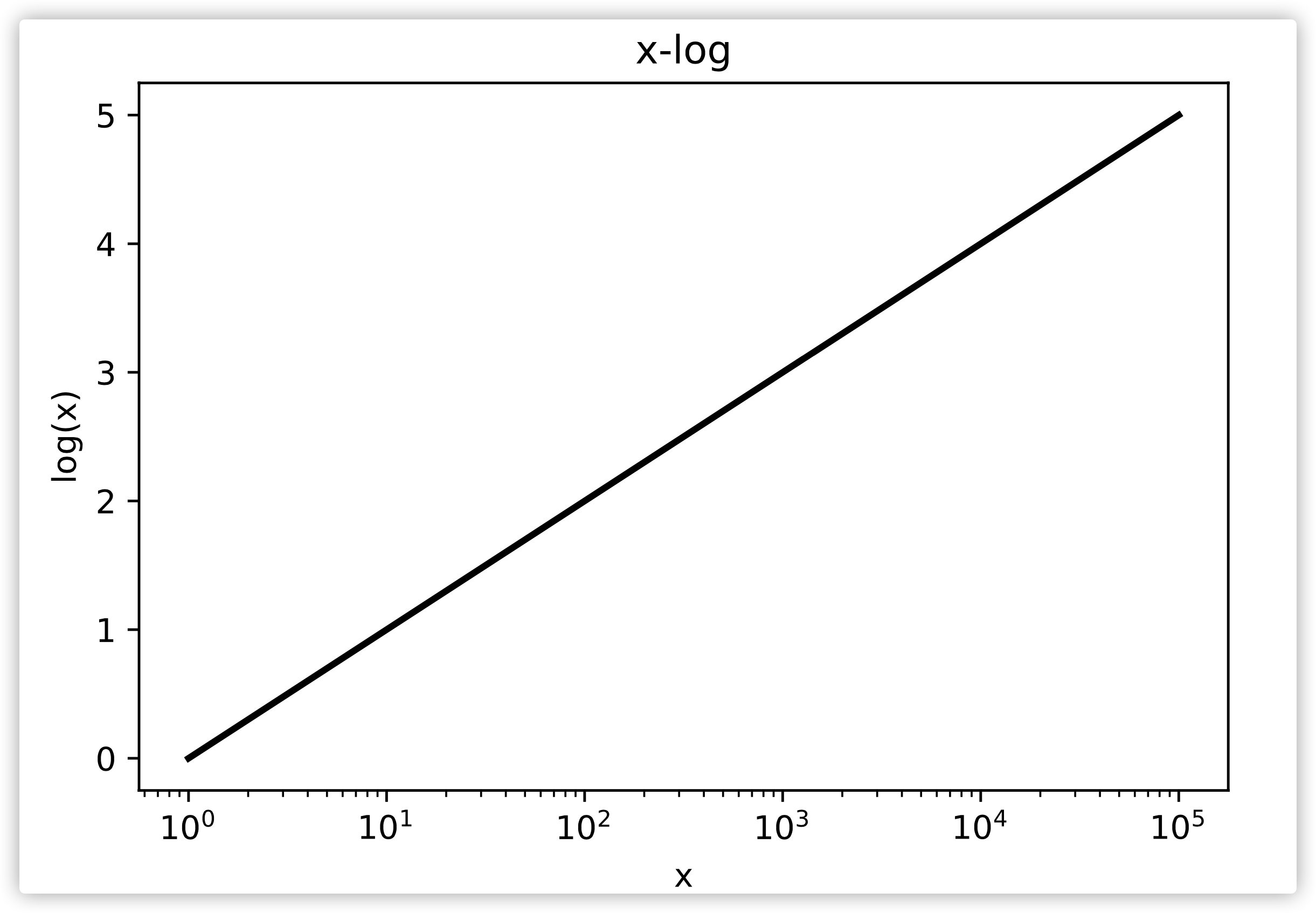
图二，对数函数在对\(x\)轴进行对数转换后的图像。
而当对\(x\)和\(y\)同时进行对数转换之后，相应的图形展示为图三。因此通常只需要将范围尺度较大的变量进行对数变换即可。
import matplotlib.pyplot as plt
import numpy as np
x = np.arange(1, 100000)
y = np.log10(x)
plt.plot(
x,
y,
color='k',
lw=2)
plt.title('xy-log')
plt.xlabel('x')
plt.ylabel('log(x)')
plt.xscale('log')
plt.yscale('log')
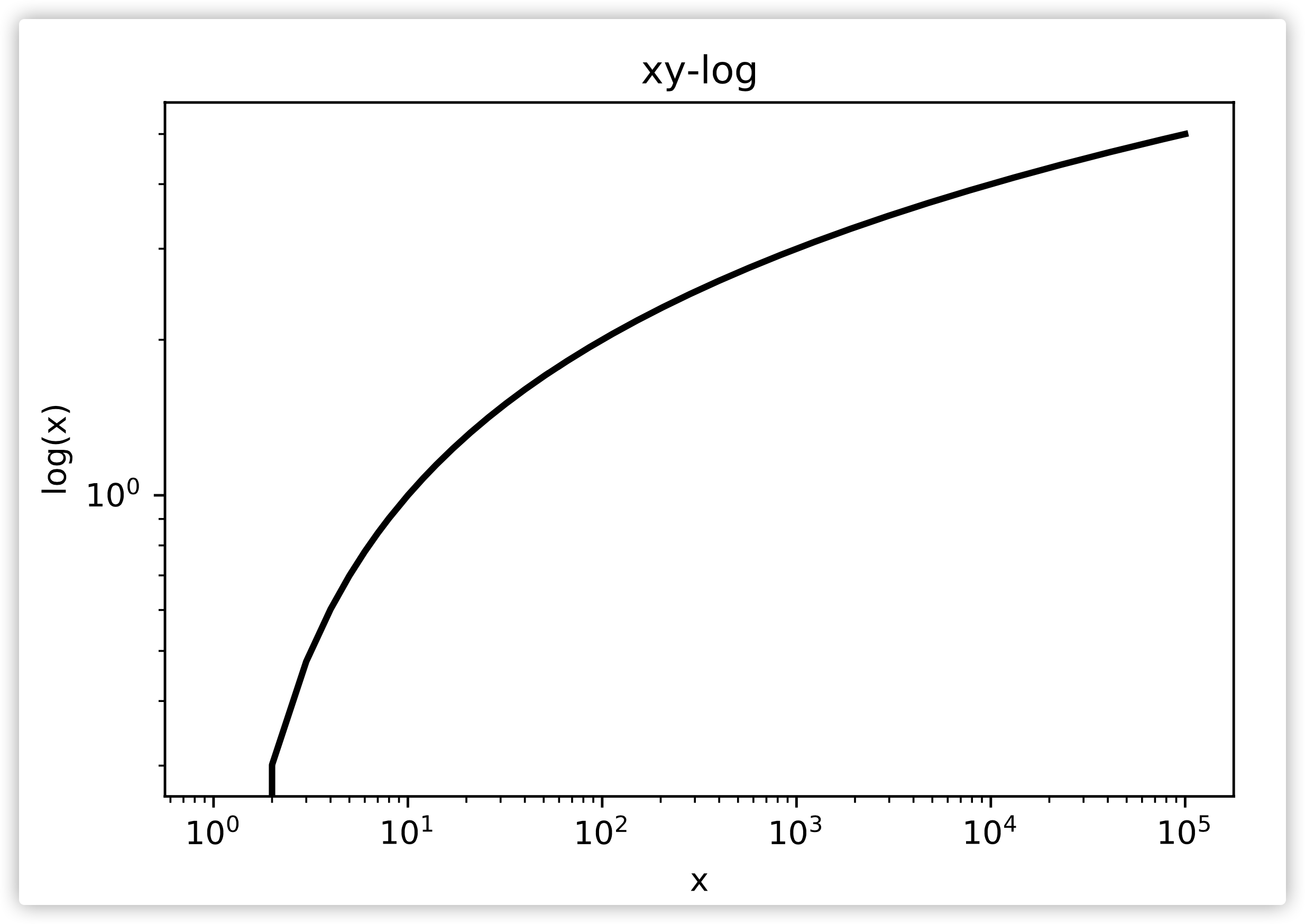
图三，对数函数在双对数坐标下的图像。
参考：
