空间独立成分分析
神经影像学当中的空间独立成分分析可以将一组被试的大脑图像在空间上分成不同的成分或网络。逻辑上按照以下流程进行:
\[\begin{pmatrix}
a_{11} & a_{a12} & \cdots & a_{in}\\
a_{21} & a_{a22} & \cdots & a_{2n}\\
\vdots & \vdots & \ddots & \vdots\\
a_{m1} & a_{m2} & \cdots & a_{mn}\\
\end{pmatrix}
=
\begin{pmatrix}
m_{11} & m_{12} & \cdots & m_{ic}\\
m_{21} & m_{22} & \cdots & m_{2c}\\
\vdots & \vdots & \ddots & \vdots\\
m_{m1} & m_{m2} & \cdots & m_{mc}\\
\end{pmatrix}
*
\begin{pmatrix}
s_{11} & s_{12} & \cdots & s_{in}\\
s_{21} & s_{22} & \cdots & s_{2n}\\
\vdots & \vdots & \ddots & \vdots\\
s_{c1} & s_{c2} & \cdots & s_{cn}\\
\end{pmatrix}
\]
- 将每位被试的影像数据逐体素转换成一行N*1;
- 把全部被试的影像逐行拼接成一个矩阵M*N;
- 将矩阵进行分解,得到混合矩阵(Mixed matrix)和源矩阵(Source matrix);
3.1. 混合矩阵为M*C,其中每一个元素表示对应被试在对应成分上的负载系数;
3.2. 源矩阵为C*N,其中每个元素表示对应成分在相应体素上的分布; - 通过混合矩阵可以得到每位被试某一成分的负载,并进行后续的统计分析;
- 通过源矩阵可以将行向量形式的体素转换到3维空间中,便于可视化(图1);
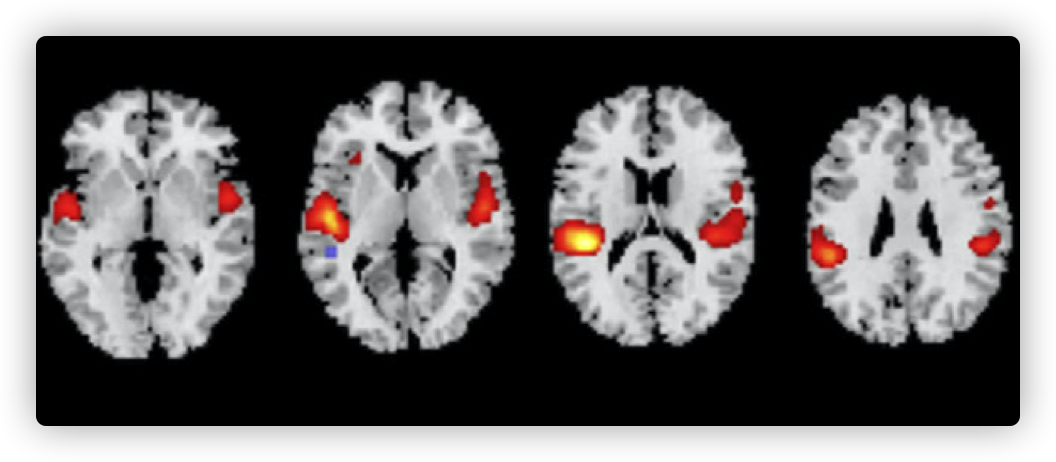
图1. 源矩阵可视化示例(Watanabe et al., Psychiatry research. Neuroimaging, 2020)。
参考
Watanabe, K., Kakeda, S., Katsuki, A., Ueda, I., Ikenouchi, A., Yoshimura, R., & Korogi, Y. (2020). Whole-brain structural covariance network abnormality in first-episode and drug-naïve major depressive disorder. Psychiatry research. Neuroimaging, 300, 111083. https://doi.org/10.1016/j.pscychresns.2020.111083



