统计之路径分析简述

一般来讲，无论是一元线性回归还是多元线性回归，都是研究自变量如何影响因变量的。然而在一些问题当中，自变量之间也有可能存在联系。这种情况下，传统的线性回归模型就不适用了。路径分析（Path Analysis）就可以解决这种问题。以下以住院的例子进行说明（图1）。

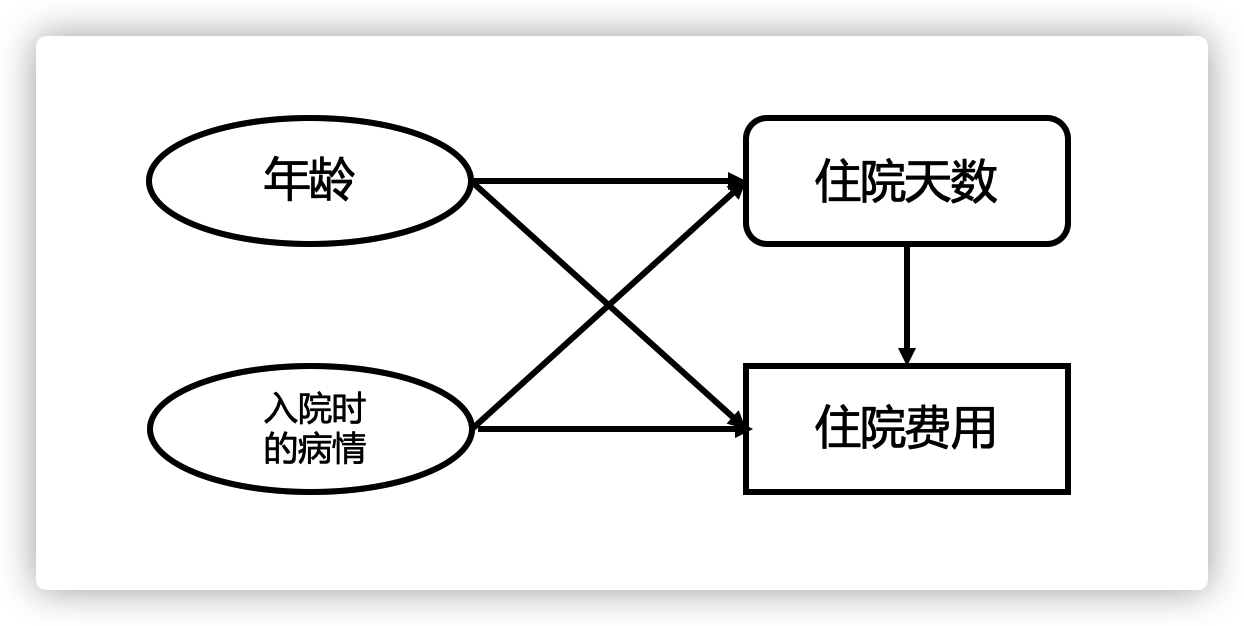
图1. 路径分析的一个例子。

年龄、入院时的病情、住院天数都会影响最终住院的费用。然而，住院天数也受到年龄和入院时病情的影响。因此对于该问题不能用线性回归模型进行分析。

路径分析的基本思路是根据学科知识对每一个非完全自变量建立线性模型。本例中，年龄和入院时的病情就是完全自变量，被称为外生变量（Exogenous Variable）。住院费用是本研究的因变量，被称为最终结果变量（Ultimate Response Variable）。而住院天数对于住院费用来讲是自变量，而对于年龄和入院时的病情来讲却又是因变量。对于这类变量，被称为内生变量（Endogenous Variable）。

路径分析建模时，首先对建立住院天数与年龄和入院时病情的线性模型，\(住院天数=年龄+入院时病情\)。然后再建立住院费用同其他变量之间的线性模型，\(住院费用=年龄+入院时病情+住院天数\)。通常在分析过程中，在不违反学科知识的情况下，会将模型中不显著的变量取消以降低模型的复杂度。

另外在最终的结果当中，由于是对两个模型同时进行分析，应当考虑标准化系数。至此，就可以得到外生变量和内生变量对于结果变量的影响了（图2）。

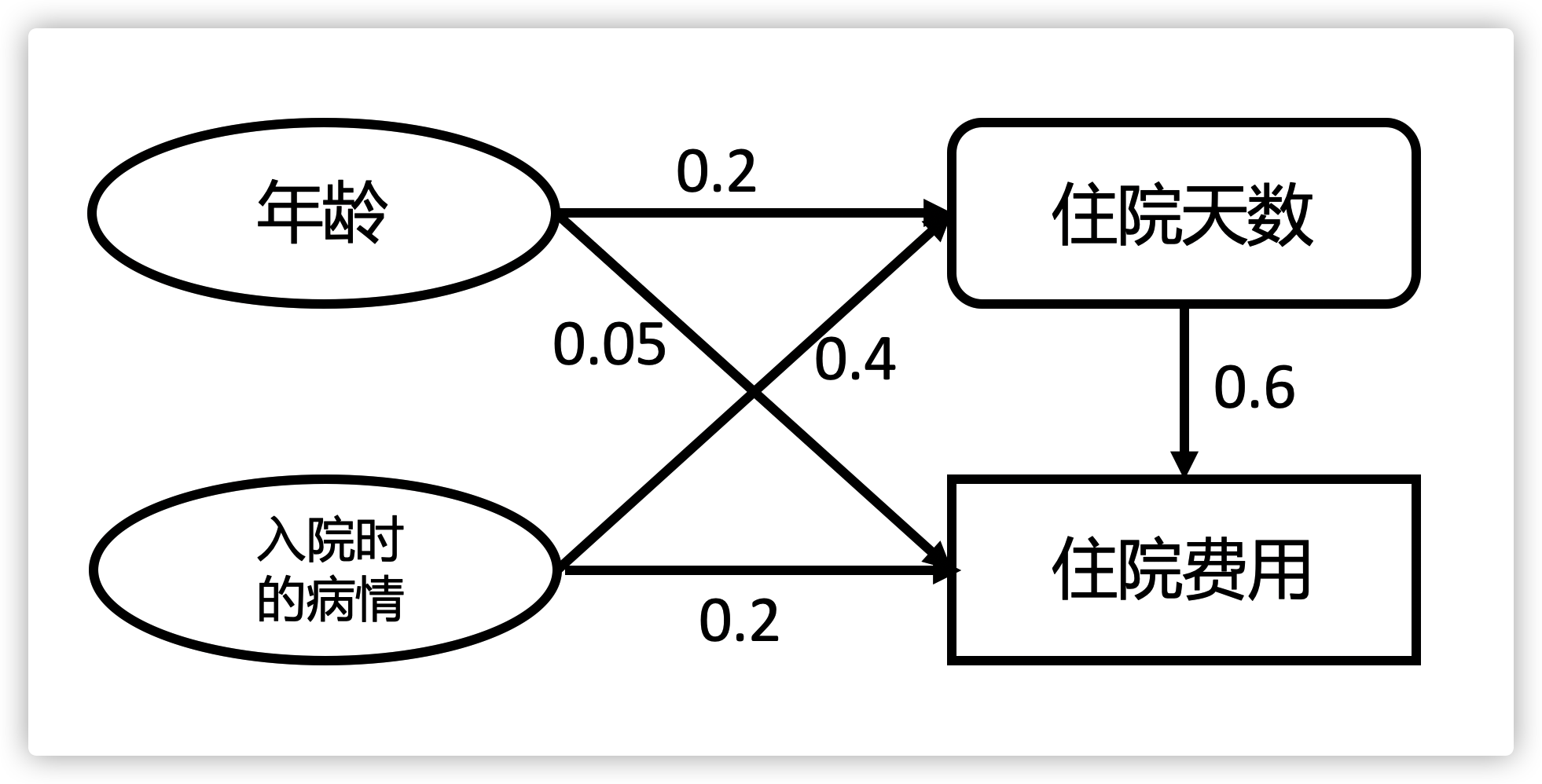
图2. 路径分析的结果呈现。图中的数值为模型中的标准化系数。数值是为了方便说明伪造的。