一颗高度为3的B+树能存多少行数据?
InnoDB存储引擎的最小储存单元是 页(Page) ,一个页的大小是默认是 16K 。磁盘存储数据最小单元是 扇区 ,一个扇区的大小是 512字节 , 而文件系统(例如XFS/EXT4)它的最小单元是 块 ,一个块的大小是 4k 。
因此InnoDB的所有数据文件(后缀为 .ibd 的文件),它的大小始终都是16384B(16k)的整数倍。
数据表中的数据都是存储在页中的,所以一个页中能存储多少行数据呢?假设一行数据的大小是1k,那么一个页可以存放16行这样的数据。
但是除了有 存放数据的页 以外,还有 存放键值+指针(索引)的页 ,即B+树中的非叶子节点,该页存放键值和指向数据页的指针,这样的页由N个(键值+指针)组成。当然它也是排好序的。 这样的数据组织形式,我们称为「索引组织表」。索引组织表通过非叶子节点的「二分查找法」以及指针确定数据在哪个页中,进而在去数据页中查找到需要的数据。
这里我们先假设B+树高为2,即存在一个根节点和若干个叶子节点,没有子页节点,那么这棵B+树的存放总记录数为:根节点指针数*单个叶子节点记录行数。
那么现在我们需要计算出非叶子节点能存放多少指针,也就是存放多少索引?
我们假设主键ID为 bigint 类型,长度为8字节,而 指针大小在InnoDB源码中设置为6字节 ,这样一共14字节。
我们一个页中能存放多少这样的单元,其实就代表有多少指针,即 16384/14=1170。一个页能存放1170个索引
那么可以算出一棵高度为2的B+树,能存放1170*16=18720条这样的数据记录。
根据同样的原理我们可以算出一个高度为3的B+树可以存放:1170(根存的记录指针数据)✖1170(下一级每个节点存的记录指针数据)✖16(每个叶子阶段存的数据条数)=21902400 条这样的记录,即2100w量级。
所以在InnoDB中B+树高度一般为1-3层,它就能满足千万级的数据存储。
在查找数据时一次页的查找代表一次 IO ,所以通过主键索引查询通常只需要1-3次 IO 操作即可查找到数据,即使一个是千万量级的表,也是很快的。
最后还有一个问题,如何得到InnoDB主键索引B+树的高度?
在InnoDB的表空间文件中,约定 page number 为 3 的代表主键索引的根页,而在根页偏移量为 64 的地方存放了该B+树的 page level 。
如果 page level 为1,树高为2, page level 为2,则树高为3。即B+树的高度=page level + 1
首先,找到MySql数据库物理文件存放位置:
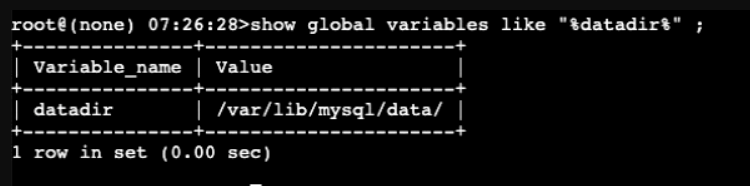
使用hexdump工具,查看表空间文件指定偏移量上的数据:

page level 值是 1,那么 B+树高度为 page level + 1 = 2



