卷积神经网络中的反向传播

卷积神经网络中的反向传播

反向传播是梯度下降法在神经网络中应用，反向传播算法让神经网络的训练成为来可能。
首先要弄清一点，神经网络的训练过程就是求出一组较好的网络权值的过程。反向传播的直观解释就是先用当前网络的权值计算结果，然后根据计算结果和真实结果的差值来更新网络的权值，使得计算结果和真实结果的差值越来越小。
当然要想准确的理解反向传播，你需要知道：梯度的概念，梯度下降法，复合函数求导的链式法则。
在多层感知机中，反向传播比较简单，要计算当前节点的误差\(\delta\)，只需要根据后一层节点的误差和当前节点的连接权重相乘后求和，如下图。

那么，在卷积神经网络中的反向传播也会和多层神经网络中的一样吗？
先来看一下多层感知机和卷积神经网络的关系：

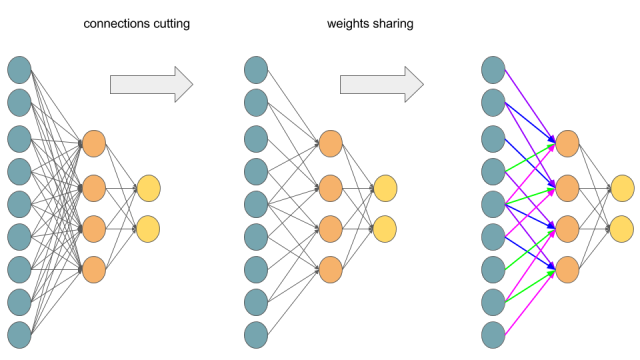
可以看到，实际上，多层感知机可以通过去除一部分的网络连接并且共享权值（上图相同颜色的连接表示，连接权值相等）转化为卷积神经网络。
可能你会说上图最右边看起来并不像一个卷积神经网络，那么请看下图：

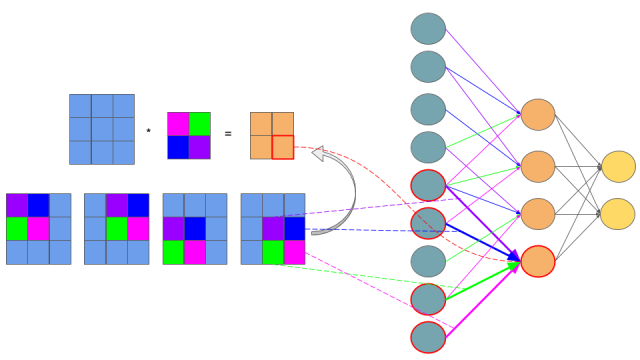
解释：

• 输入层的9个节点是3×3原始图像的9个像素
• 卷积核是2×2大小的，用4种颜色表示不同位置
• 3×3图像经过2×2卷积操作后得到2×2图像，即网络中间层的4个节点。
• 四个角的像素各自只参与一次卷积计算，因此只有一条连接到下一层节点，而中间位置的像素参与4次卷积计算，到下一层节点有四个连接。

所以，在卷积神经网络（CNN）的反向传播的节点误差\(\delta\)也可以像之前的多层感知机一样计算：

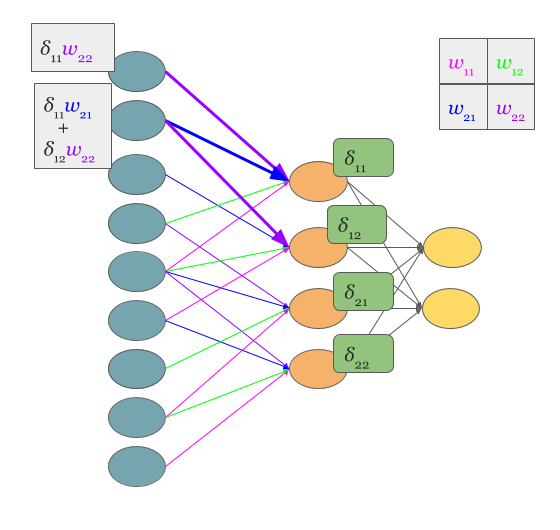
通常，为了便于计算，反向传播计算误差时同样使用卷积来表示，这时需要将卷积核做180度旋转（原因见下面公式推导）：


在前向计算的过程中，使用的是valid卷积方式，卷积操作的对象是前一层的输出，而在后向传播中使用的full卷积方式，卷积操作的对象是后一层传回的误差。
接下来会进行一些公式推导：
在多层感知机中，第\(l\)层节点\(j\)的误差(偏导)为：\(\delta^l_j = \frac{\partial C}{\partial z^l_j}\)，

其中：$z^{l_j}= \sum\limits_{k} w^l_{jk} a^{l-1}_k + b^l_j $，

令\(a_j^l = \sigma(z_j^l)\)

其中\(\sigma\)表示sigmoid, tanh或者relu等激活函数。
在卷积神经网络中，使用\(z_{x,y}\)代替\(z_{j}\),得到前向过程的卷积计算\(z_{x,y}^{l+1} = w^{l+1} * \sigma(z_{x,y}^l) + b_{x,y}^{l+1} = \sum \limits_{a} \sum \limits_{b} w_{a,b}^{l+1}\sigma(z_{x-a,y-b}^l)+ b_{x,y}^{l+1}\)，
在卷积神经网络中节点\(j\)的偏导为：$ \delta_{x,y}^l = \frac{\partial C}{\partial z_{x,y}^l} =\sum \limits_{x'} \sum \limits_{y'}\frac{\partial C}{\partial z_{x',y'}^{l+1}}\frac{\partial z_{x',y'}^{l+1}}{\partial z_{x,y}^l}\( 而\)z_{x,y}^{l$的误差是由$z_{x,y}}$传导而来，因此使用链式法则有：

\[\frac{\partial C}{\partial z_{x,y}^l} =\sum \limits_{x'} \sum \limits_{y'}\frac{\partial C}{\partial z_{x',y'}^{l+1}}\frac{\partial z_{x',y'}^{l+1}}{\partial z_{x,y}^l} = \sum \limits_{x'} \sum \limits_{y'} \delta_{x',y'}^{l+1} \frac{\partial(\sum\limits_{a}\sum\limits_{b}w_{a,b}^{l+1}\sigma(z_{x'-a, y'-b}^l) + b_{x',y'}^{l+1})}{\partial z_{x,y}^l} \]

由于只有下标为\(x=x'-a\)和\(y=y'-b\)的项的误差会传给\(z_{x,y}^l\)，其它项的偏导为０，所以$$ \sum \limits_{x'} \sum \limits_{y'} \delta_{x',y'}^{l+1} \frac{\partial(\sum\limits_{a}\sum\limits_{b}w_{a,b}^{l+1}\sigma(z_{x'-a, y'-b}^l) + b_{x',y'}^{l+1})}{\partial z_{x,y}^l} = \sum \limits_{x'} \sum \limits_{y'} \delta_{x',y'}^{l+1} w_{a,b}^{l+1} \sigma'(z_{x,y}^l)$$
而当\(x=x'-a\)和\(y=y'-b\)时，有\(a=x'-x\)，\(b=y'-y\)，所以上式可以写成

\[\sum \limits_{x'} \sum \limits_{y'} \delta_{x',y'}^{l+1} w_{a,b}^{l+1} \sigma'(z_{x,y}^l) =\sum \limits_{x'}\sum \limits_{y'} \delta_{x',y'}^{l+1} w_{x'-x,y'-y}^{l+1} \sigma'(z_{x,y}^l)=\delta^{l+1} * w_{-x,-y}^{l+1} \sigma'(z_{x,y}^l) \]

上式中\(rot_{180^\circ}(w_{x,y}^{l+1}) = w_{-x, -y}^{l+1}\)，因此在反向传播计算误差时需要将卷积核旋转180°
接下来计算误差受权值\(w_{a,b}^l\)的影响$\frac{\partial C}{\partial w_{a,b}^l} $

\[\frac{\partial C}{\partial w_{a,b}^l} = \sum \limits_{x} \sum\limits_{y} \frac{\partial C}{\partial z_{x,y}^l}\frac{\partial z_{x,y}^l}{\partial w_{a,b}^l} = \sum \limits_{x}\sum \limits_{y}\delta_{x,y}^l \frac{\partial(\sum\limits_{a'}\sum\limits_{b'}w_{a',b'}^l\sigma(z_{x-a', y-b'}^l) + b_{x,y}^l)}{\partial w_{a,b}^l} \]

\[=\sum \limits_{x}\sum \limits_{y} \delta_{x,y}^l \sigma(z_{x-a,y-b}^{l-1}) = \delta_{a,b}^l * \sigma(z_{-a,-b}^{l-1}) =\delta_{a,b}^l * \sigma(rot_{180^\circ}(z_{a,b}^{l-1})) \]

所以在卷积神经网络中的训练过程如下：

1. 输入x
2. 前向过程：对每一个网络层l=2,3, …,L，计算$ z_{x,y}^l = w^l * \sigma(z_{x,y}^{l-1}) + b_{x,y}^l ， a_{x,y}^l = \sigma(z_{x,y}^l)$
3. 输出误差\(\delta^L\)：计算向量$ \delta^L = \nabla_a C \odot \sigma'(z^L)$
4. 误差反向传播：对每一个网络层l=L-1,L-2,…,2，计算\(\delta_{x,y}^l =\delta^{l+1} * rot_{180^\circ}(w_{x,y}^{l+1}) \sigma'(z_{x,y}^l)\)
5. 根据梯度更新参数：成本函数的梯度由下式给出$ \frac{\partial C}{\partial w_{a,b}^l} =\delta_{a,b}^l * \sigma(rot_{180^{\circ}(z_{a,b}})) $

References:
Convolutional Neural Networks backpropagation: from intuition to derivation
Backpropagation In Convolutional Neural Networks