信息量、信息熵、相对熵、交叉熵

一般使用交叉熵作为损失函数时，在模型的输出层总会接一个softmax函数，这是为什么呢？

交叉熵简介：

交叉熵是信息论中的一个重要概念，主要用于度量两个概率分布间的差异性，要理解交叉熵，需要先了解以下几个概念。

信息量

信息奠基人香农（Shannon）认为“信息是用来消除随机不确定性的一种东西”，也就是说衡量信息量的大小就是看这个信息消除不确定性的程度。

“太阳从东边升起”，这条信息并没有减少不确定性，因为太阳肯定是从东边升起的，这是一句废话，信息量为0.

“2018年中国队成功进入世界杯”。从直觉上来看，这句话具有很大信息量。因为中国队进入世界杯的不确定性因素很大。而这句话消除了进入世界杯的不确定性，所以按照定义，这句话的信息量很大。

根据上述描述，总结如下：信息量的大小与信息发生的概率成反比。概率越大，信息量越小。概率越小，信息量越大。

设某一事件发生的概率为P(x)，其信息量表示为：

I(x)=−log(P(x))

其中I(x)表示信息量，这里log表示以e为底的自然对数。

信息熵

信息熵也被成为熵，用来表示所有信息量的期望。

在概率论和统计学中，数学期望(mean)（或均值，亦简称期望）是试验中每次可能结果的概率乘以其结果的总和，是最基本的数学特征之一。它反映随机变量平均取值的大小。

所以信息量的熵可以表示为：（这里的X是一个离散型随机变量）

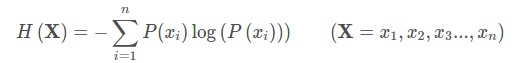
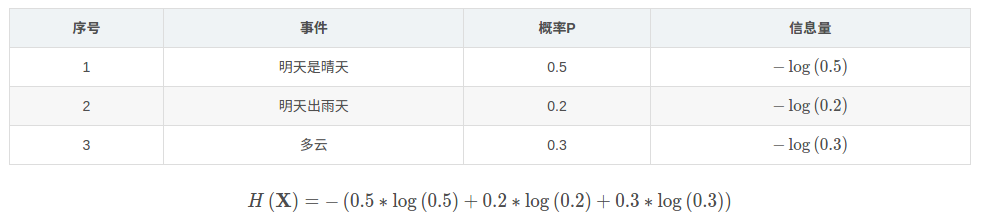
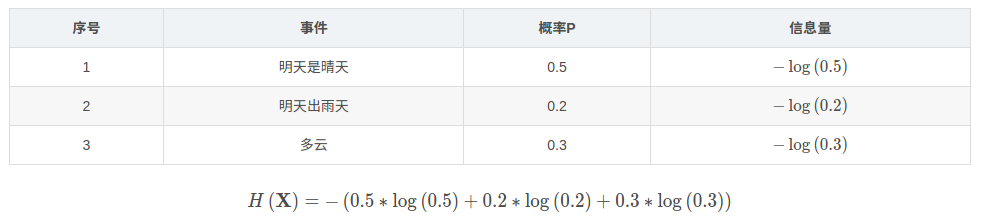
使用明天的天气概率来计算其信息熵:

对于0-1分布问题，由于其结果只用两种情况，是或不是，设某一事件发生的概率为P(x)，则另一事件发生的概率为1 - P(x)，所以对于0-1分布问题，计算熵的公式可以简化如下：

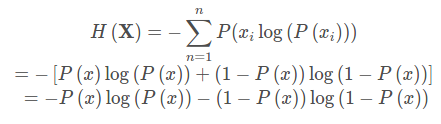
相对熵（KL散度）：

如果对于同一个随机变量X有两个单独的概率分布P(x)和Q(x)，我们可以使用KL散度来衡量这两个概率分布之间的差异。

下面直接列出公式，再举例加以说明：

在机器学习中，常常使用P(x)来表示样本的真实分布，Q(x)表示模型所预测的分布，比如在一个三分类任务中（例如，猫马狗分类器），x1，x2，x3分别代表猫，马，狗。例如一张猫图片的真实分布P(X)= [1， 0，0]，预测分布 Q ( X ) = [ 0.7 , 0.2 , 0.1 ]，计算KL散度：

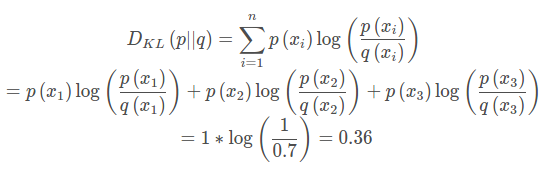
KL散度越小，表示P(x)与Q(x)的分布更加接近，可以通过反复训练Q(x)来使Q(x)的分布逼近P(x)。

交叉熵

首先将KL散度公式拆开：

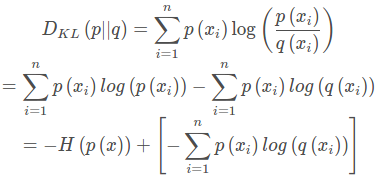
前面的H（p(x)）表示信息熵，后面的中括号内容表示交叉熵。KL散度 = 信息熵 - 交叉熵

交叉熵公式表示为：

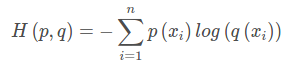
在机器学习训练网络时，输入数据与标签常常已经确定，那么真实概率分布 P ( x )也就确定下来了，所以信息熵在这里就是一个常量。由于KL散度的值表示真实概率分布 P ( x )与预测概率分布 Q ( x ) 之间的差异，值越小表示预测的结果越好，所以需要最小化KL散度，而交叉熵等于KL散度加上一个常量（信息熵），且公式相比KL散度更加容易计算，所以在机器学习中常常使用交叉熵损失函数来计算loss就行了。

交叉熵在单分类问题中的应用：

在线性回归问题中，常常使用MSE（Mean Square Error）作为loss函数，而在分类问题中常常使用交叉熵作为损失函数。

下面使用一个例子来说明如何计算交叉熵损失值，假设我们输入一个狗的图片，标签与预测值如下：

其中， m表示样本个数。

Summary：

（1）交叉熵能够衡量同一个随机变量中的两个不同概率分布的差异程度，在机器学习中就表示为真实概率分布与预测概率分布之间的差异。交叉熵的值越小，模型预测效果越好。

（2）交叉熵在分类问题中，常常与softmax是标配，softmax将输出结果进行处理，使其多个分类预测值总和为1，再通过交叉熵来计算损失。