软工作业--结对编程

目录

• 结对编程
• PSP表格：
• 效能分析
  • 皆在 -n 10000 -r 10 前提下测试
    • 第一部分-完成自动生成小学四则运算
    • 第二部分-对给定的题目文件、答案文件有统计对错功能
• 设计实现过程
  • 第一部分--完成自动生成小学四则运算
    • 设计思路
    • 函数说明
  • 第二部分--对给定的题目文件、答案文件有统计对错功能
    • 函数说明
• 代码展示
  • 运算数统一结构
  • 第一部分---完成自动生成小学四则运算
    • 代码展示
  • 第二部分---对给定的题目文件、答案文件有统计对错功能
• 测试运行
  • 运行参数规范
  • 单元测试
• 项目小结
  • 分享经验和教训总结
  • 成败得失总结

结对编程

软工作业	结对编程
作业要求	作业链接
队伍成员	3218005445周赛星、3118005412胡晓煜
github	Pair-programming
作业目标	实现一个自动生成小学四则运算题目的命令行程序，以及对给定的题目文件、答案文件有统计对错功能。

---

分工	功能实现
3118005412胡晓煜	实现自动生成小学四则运算题目
3218005445周赛星	实现对给定的题目文件、答案文件的统计对错功能

PSP表格：

PSP2.1	Pair-programming Process Stages	预估耗时（h）	实际耗时（h）
Planning	计划	2	4
Estimate	估计这个任务需要多少时间	24	32
Development	开发	4	6
Analysis	需求分析（包括学习新技术）	1	6
Design Spec	生成设计文档	1	1.5
Design Review	设计复审	0.5	1
Coding Standard	代码规范（为目前的开发制定合适的规范）	0.5	1
Design	具体设计	1	3
Coding	具体编码	7	9
Code Review	代码复审	1	1.5
Test	测试（自我测试，修改代码，提交修改）	2	6
Reporting	报告	2	1
Test Report	测试报告	2	2
Size Measurement	计算工作量	1	1.8
Postmortem&Process Improvement Plan	事后总结，并提出过程改进计划	1	2
.	合计	50	77.8

效能分析

皆在 -n 10000 -r 10 前提下测试

第一部分-完成自动生成小学四则运算

CPU占比

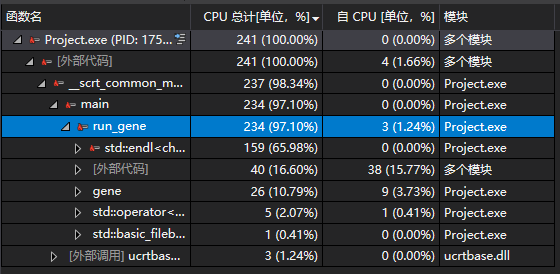
内存占比

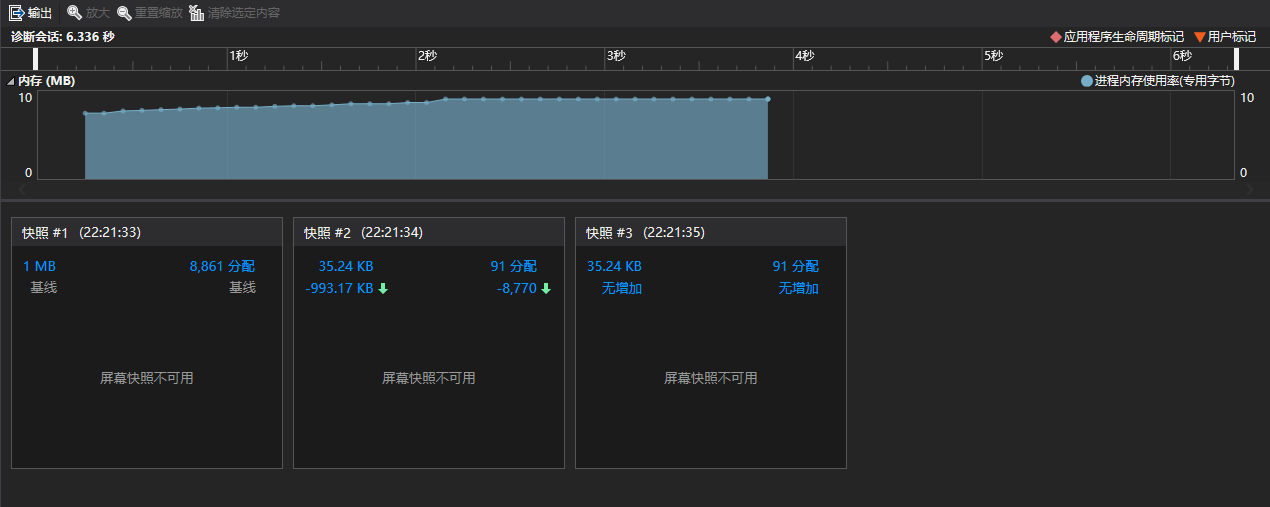
时间占比：标准库函数调用次数较多，时间占比较高。

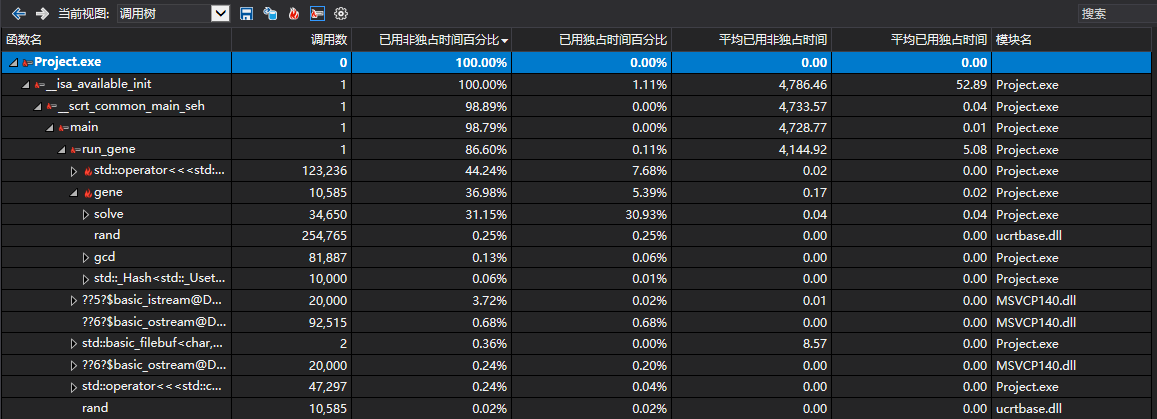
实测结果

第二部分-对给定的题目文件、答案文件有统计对错功能

CPU占比

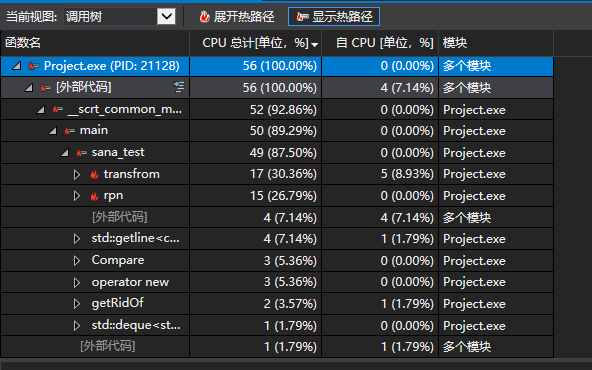
内存占比

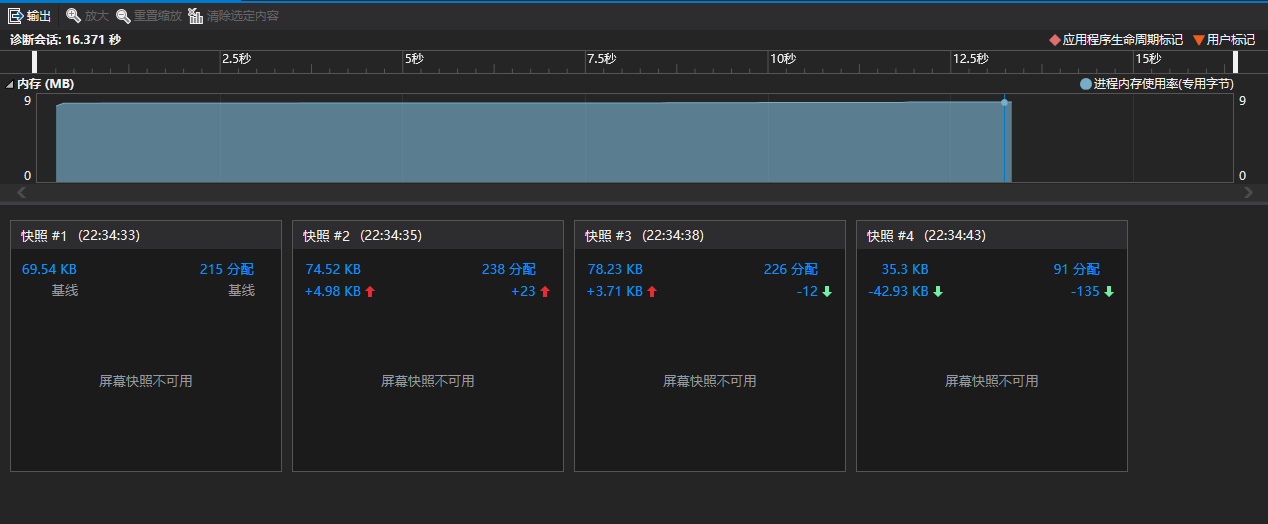
时间占比

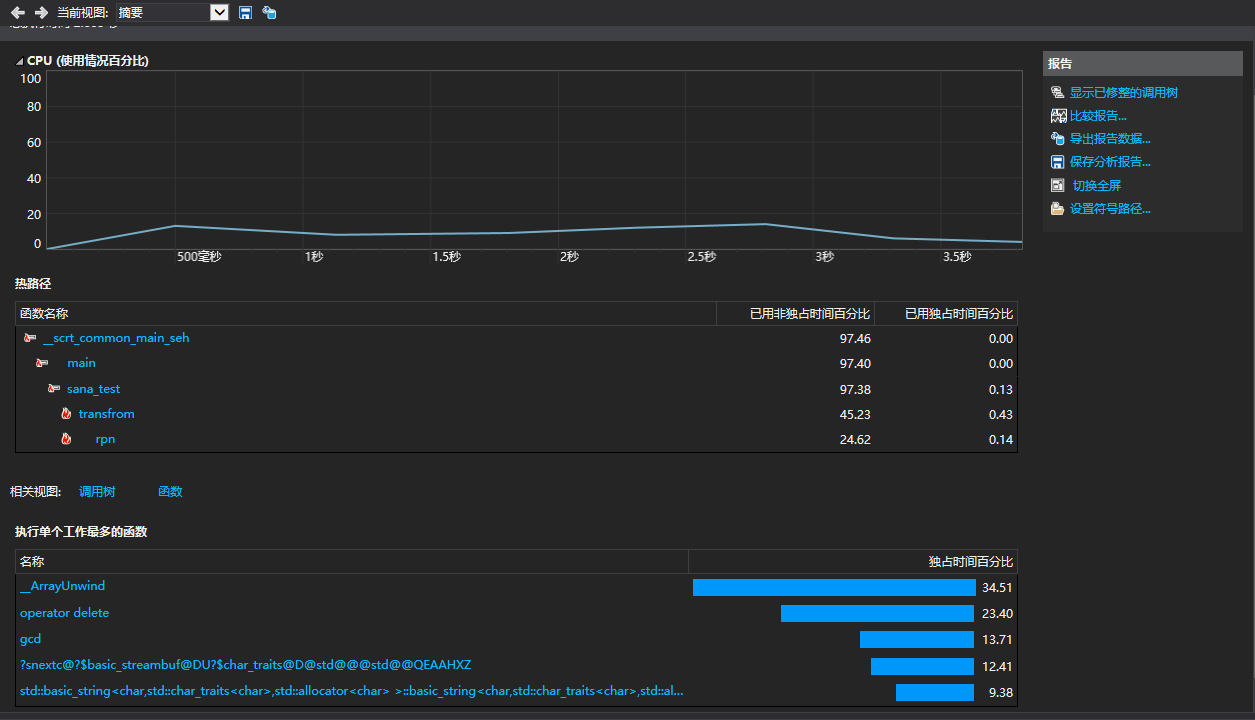
实测结果

设计实现过程

运算数结构体Frac

皆以不可约分子形式存在
重载 +、-、*、/ 运算符

typedef long long LL

第一部分--完成自动生成小学四则运算

设计思路

1.先考虑不包含括号的情况，显然只需要随机生成合法运算数和运算符，在运算时判断一下生成的式子是否符合要求即可。运算规则按照先乘除后加减从左到右运算，乘除部分在做除法时需要判定是否存在除0问题，加减部分需要先减后加来排除运算过程存在子表达式为负数的情况。由运算规则知用链表模拟就行，运算时合并结点，链表结点主要包含运算数和运算符。

2.再考虑有括号的情况，当生成括号时需要进入括号内进行子运算，运算完后整个括号返回来时等效于一个运算数(实际上为链表结点)，之后再按第1种情况处理。

3.由上可知，此算法的过程相当于模拟手动运算，因此能保证正确性。使用哈希表维护运算结果不重复来排除生成题目的重复问题。

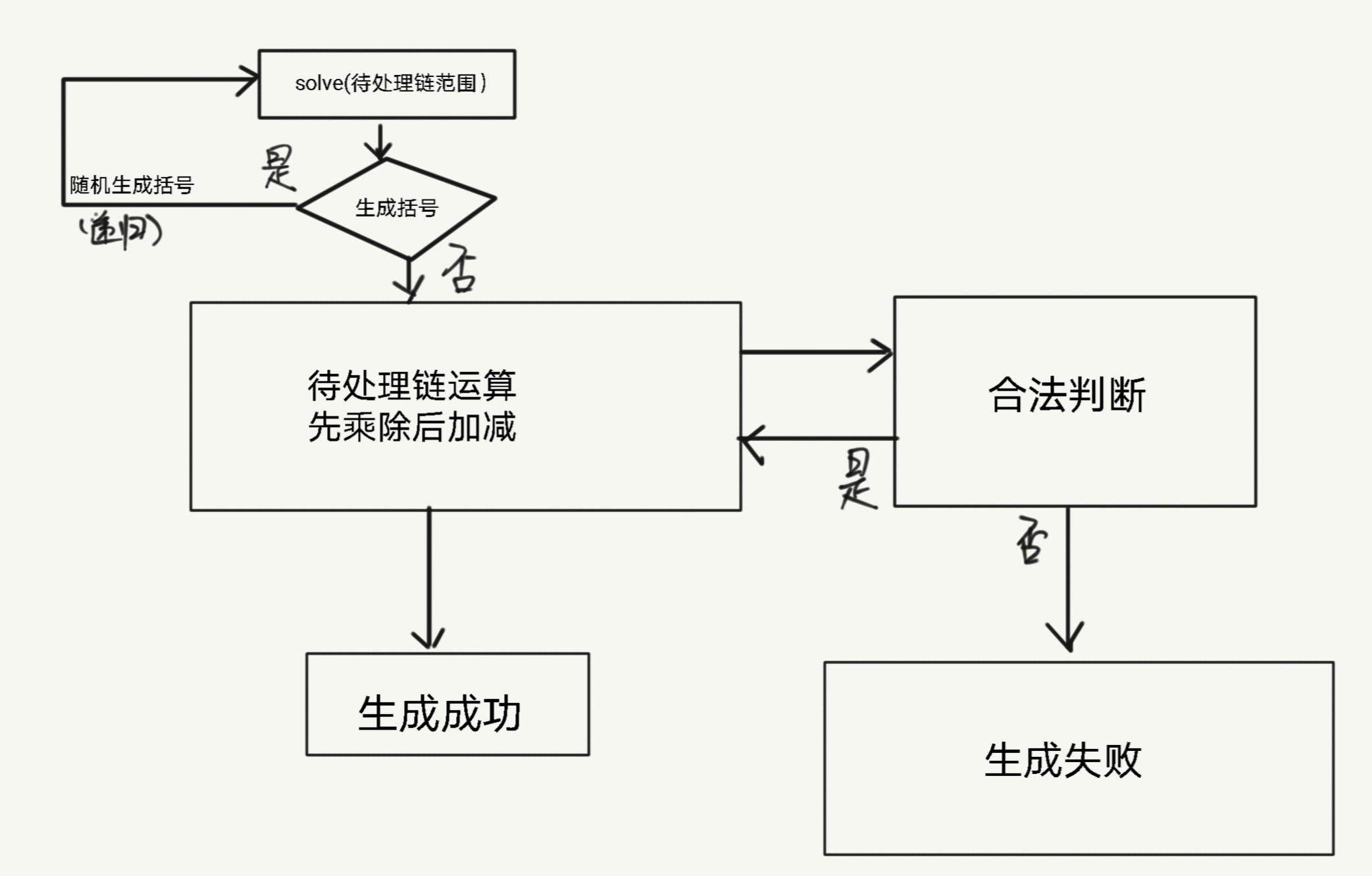
函数说明

bool solve(int s, int n, bool is_brack) { ... }

1.参数：待处理链范围(详情看代码展示部分)，是否生成括号

2.返回值：生成算术表达式是否合法

3.具体功能：生成功能核心函数，总思路的实现，主要包括生成括号与运算生成的算术表达式

bool gene(int n, int m) { ... }

1.参数：生成算术表达式的项数、生成数值大小上限

2.返回值：是否成功生成算术表达式

3.具体功能：随机生成合法运算数和运算符并调用solve函数检验

bool run_gene(int t, int m) { ... }

1.参数：生成算术表达式的个数、生成数值大小上限

2.返回值：是否成功生成t个算术表达式

3.具体功能：负责迭代调用gene生成算术表达式并做输出处理

第二部分--对给定的题目文件、答案文件有统计对错功能

运算符号优先级：“（”，“）” < “+” < “-” < “×” < “÷”

函数说明

string getRidOf(string str); 

1、参数：文件读入的运算式或答案
2、返回值：处理后的运算式或答案
3、具体功能：去除字符串开头的序号和空格

bool is_operator(string op); 

具体功能：判断是否为操作符（“+”、“-”、“*”、“/”、“(”、“)”）

int get_priority(string op);

具体功能：判断优先级，“（”、“）” < “+” < “-” < “*” < “/”

Frac transfer(string val); 

1、参数：string类型表示的运算数或答案
2、返回值：Frac类型
3、具体功能：将字符串val转换成Frac类型

string llTostr(LL num); 

1、参数：LL类型表示的数
2、返回值：string类型
3、具体功能：LL类型num转换成string类型

string get_result(string val1, string val2, string op);

1、参数：两个运算数和一个运算符
2、返回值：string类型
3、具体功能：逆波兰式子运算调用

bool Compare(string result, string refer); 

具体功能：运算值和答案值比较

stack<string> transfrom(string input);

1、参数：经处理后的运算式
2、返回值：该运算式的逆波兰式，用string类型栈存储返回
3、具体功能：运算式转换波兰式，调用is_operator(...)判断读入字符是否为操作数，调用get_priority(...)判断运算符优先级，控制运算符压的入栈顺序

string rpn(stack<string> _stk); 

1、参数：string类型栈--存储运算式逆波兰式
2、返回值：string类型表示的运算式结果
3、具体功能：波兰式运算，调用get_result(...)进行子运算并将结果值压入中间栈

代码展示

运算数统一结构

struct Frac {
	LL up, down;  //均以分数形式
	Frac();
	Frac(LL x, LL y);
	Frac operator + (const Frac& x) const;
	Frac operator - (const Frac& x) const;
	Frac operator * (const Frac& x) const;
	Frac operator / (const Frac& x) const;
	bool operator == (const Frac& x) const;
};

第一部分---完成自动生成小学四则运算

代码展示

核心函数的实现

总体分三部分：生成括号->先乘除->再加减

详情看注释

//当前起始节点为s 往下走n步为终止结点 是否生成括号
//返回值：是否成功生成算术表达式
bool solve(int s, int n, bool is_brack) {
    //生成括号
	while (n > 1 && is_brack) {
        //生成括号范围
		int l = rand() % n;
		int r = rand() % n + 1;
		while (l >= r || r == n && l == 0) r = rand() % n + 1;
		int _l = s;
		for (int i = 0; i < l; i++) _l = nex[_l];
		int _r = s;
		for (int i = 0; i < r; i++) _r = nex[_r];
        //记录括号位置
		brack[itvl[_l]][0]++;
		brack[itvr[_r]][1]++;
		n -= r - l;
        //递归处理括号运算
		if (!solve(_l, r - l, rand() & 1)) return false;
		itvr[_l] = itvr[_r];
        //重置生成括号信号
		is_brack = rand() & 1;
	}
	int temp;
	//先乘除
	temp = s;
	for (int i = 0; i < n; i++, temp = nex[temp]) {
		while (i < n && (sign[temp] == '*' || sign[temp] == '/')) {
			if (sign[temp] == '*')
				num[temp] = num[temp] * num[nex[temp]];
			if (sign[temp] == '/') {
				if (num[nex[temp]].up == 0) return false;
				num[temp] = num[temp] / num[nex[temp]];
			}
			sign[temp] = sign[nex[temp]];
			nex[temp] = nex[nex[temp]];
			n--;
		}
	}
	//减
	temp = s;
	for (int i = 0; i < n; i++, temp = nex[temp]) {
		while (i < n && sign[temp] == '-') {
			num[temp] = num[temp] - num[nex[temp]];
			if (num[temp].up < 0 || num[temp].down < 0) return false;
			sign[temp] = sign[nex[temp]];
			nex[temp] = nex[nex[temp]];
			n--;
		}
	}
	//加
	temp = s;
	for (int i = 0; i < n; i++, temp = nex[temp]) {
		while (i < n) {
			num[temp] = num[temp] + num[nex[temp]];
			sign[temp] = sign[nex[temp]];
			nex[temp] = nex[nex[temp]];
			n--;
		}
	}
	return true;
}

第二部分---对给定的题目文件、答案文件有统计对错功能

1、对读入的题目和答案进行处理，仅留下题目和答案。

例如：
题目读入 1. (4/5 + 6/7 - 1/7 ) * 4
答案读入 2. 1'18/35
处理之后
题目为 (4/5 + 6/7 -1/7) * 4
答案为 1'18/35

2、将题目转换成逆波兰式存储到string类型栈中

以上题为例

逆波兰式转换

stack<string> transfrom(string input) {
	stack<string> converted;
	stack<string> op;
	int i = 0;
	string digit_node = "";

	while (i < input.length()) {

		char c = input[i];
		string read_char = "";
		read_char += c;

		//扩展识别 ×和÷
		if (input[i] == (char)0xC3) {
			if (input[++i] == (char)0x97) read_char = "*";
			else read_char = "/";
		}
		if (is_operator(read_char)) {  //is_operator()用于检查符号是否为 '+', '-', '*', '/','(',')'
			if (digit_node != "") { //每次判别有符号要入栈时，都把之前所积累的运算数压入栈。
				converted.push(digit_node);
				digit_node = "";
			}
			if (op.empty()) {  //若装运算符的栈空，直接入栈
				op.push(read_char);
			}
			else {
				//此种情况为装运算符的栈不为空的情况
				if (read_char == "(")  //若读入符号是左括号，那么直接入栈
					op.push(read_char); 
				else if (read_char == ")") {  //若读入符号是右括号，需要把 与op栈内最近的左括号 之间的运算符入栈converted中。
					while (op.top() != "(") {   
						converted.push(op.top());
						op.pop();
					}
					op.pop();
				}
				else if (get_priority(read_char) > get_priority(op.top())) //比较优先级，优先级(高-->低)：( "(",")" ),"+","-","×","÷"
					op.push(read_char);
				else if(get_priority(read_char) == get_priority(op.top())){
					if (read_char == "-") {
						converted.push(op.top());
						op.pop();
						op.push(read_char);
					}
					else if (read_char == "/") {
						converted.push(op.top());
						op.pop();
						op.push(read_char);
					}
					else{
						op.push(read_char);
					}
				}
				else {
					while (!op.empty()&& (get_priority(op.top()) > get_priority(read_char)|| get_priority(op.top()) == get_priority(read_char))) {
						if ((get_priority(op.top()) > get_priority(read_char))) {
							converted.push(op.top());
								op.pop();
						}
						else if (get_priority(op.top()) == get_priority(read_char)) {
							if (read_char == "-"|| read_char == "/") {
								converted.push(op.top());
								op.pop();
							}
							else {
								break;
							}
						}
					}
					op.push(read_char);
				}
			}
			i++;
		}
		else { //若读入符号是数字
			int j = i;
			while (input[j]!=')'&&input[j] != ' '&&j<input.length()&&input[j]!='=') { //input[j]!=' '--针对读取分数截止是后一个符号是空，
				digit_node += input[j];				 //input[j]!='\0' --针对读取分数时最后一个分数，此时截止情况可能不是空，是'\0'。
				j++;
			}
			i = j;  
			if (input[i] != ')') i++;
		}
		
	}

	if (digit_node != "") { 
		converted.push(digit_node);
	}
	while (!op.empty()) {
		converted.push(op.top());
			op.pop();
	}
	//将位置倒置一下，方便后期运算 
	stack<string> stk;
	while (!converted.empty()) {
		stk.push(converted.top());
		converted.pop();
	}

	return stk;
}

3、进行运算

第二步骤返回string类型栈stack1--存有题目的逆波兰式，新创一个string类型栈stack2--存放运算数以及中间值。
当stack1不为空时，栈顶出栈判断，若是运算数，则压入stack2中；若是运算符，则stack2栈顶出栈两次，与运算符运算后将结果压入stack2中。
返回stack2.top()

波兰式运算

string rpn(stack<string> _stk) { //_stk--运算式逆波兰式
stack<string> rs;
while (!_stk.empty()) {
if (is_operator(_stk.top())) {
string val1 = rs.top();
rs.pop();
string val2 = rs.top();
rs.pop();
string op = _stk.top();
_stk.pop();
rs.push(get_result(val2, val1, op)); //由于入栈的顺序，val2才是第一运算数。
}
else {
rs.push(_stk.top());
_stk.pop();
}
}
return rs.top();
}

4、与答案进行比较

运算结果值与读入的答案做比较，记录对错和题号。

测试运行

运行参数规范

例：
Project.exe -n (0,100000] -r (0,10000]
project.exe -e <exercisefile>.txt -a <answerfile>.txt

单元测试

前提：已对生成函数和校对函数做过手动验证均正确

此单元测试为互拍验证，即生成后进行自身校对

测试模板代码如下：

TEST_METHOD(TestMethod2)
{
	run_gene(10, 10);
	sana_test(adr_exe, adr_ans);
	int ans = get();
	Assert::AreEqual(10, ans);
}
TEST_METHOD(TestMethod9)
{
	run_gene(99999, 1000);
	sana_test(adr_exe, adr_ans);
	int ans = get();
	Assert::AreEqual(99999, ans);
}

测试样例总共分10组：

	-n	-r
0	10	3
1	10000	6
2	10	10
3	10	100
4	10	1000
5	10000	10
6	10000	100
7	10000	1000
8	99999	10
9	99999	1000

结果如下：

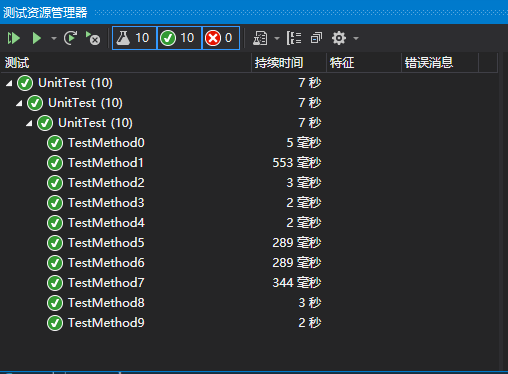
项目小结

分享经验和教训总结

共用的模块设计需满足各自的功能实现。
程序实现过程中队友们应多多交流想法，方便理解和提出建议。
前期工作准备中需对程序要求咬文嚼字，了解透彻，避免出现理解上的二义性。
在四则运算的校正功能中需要考虑到加减乘除的运算特性。
代码审核很重要，尽量在审核代码时找出逻辑错误，可以减少大量debug时间。
四则运算的校正功能由于是通过逆波兰式实现运算，相当于从右往左运算，就需考虑到运算式连减、连除、先除后乘、无括号情况中连减中出现除法和连除中出现减法等特殊情况的运算顺序不可改变。
实现时不需要太局限于字面上的功能要求，可以在此基础上进行扩展。

成败得失总结

仅实现命令行程序，未实现图形界面。
算术表达式结果唯一虽保证题目不重复但会限制题目生成空间。

成员	结对感受	对彼此的闪光点或建议
3218005445周赛星	功能实现上可以和搭档探讨，梳理思路。	很有耐心，给了我充足的思想空间和实现时间； 很细心，对程序的实现要求了解透彻，对问题的阐述清晰；很有计划和前瞻性；思维缜密。
3118005412胡晓煜	和搭档讨论思路能更快发现存在的漏洞，加速开发进程。	自主性强，思维清晰，善于发现问题，编程能力有待提升。