js递归实现斐波那契数列及优化

斐波那契数列：
斐波那契数列指的是这样一个数列：

“ 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233，377，610，987，…”

这个数列从第3项开始，每一项都等于前两项之和。

递归求斐波那契数列
​ 这个函数的功能是求任意项的斐波那契数列

  //统计计算次数
        let count = 0

        function fibNumber(n) {
            count++
            if (n == 1 || n == 2)
                return 1

            return fibNumber(n - 1) + fibNumber(n - 2)
        }

        console.log(fibNumber(40))
        console.log(count)

 

 

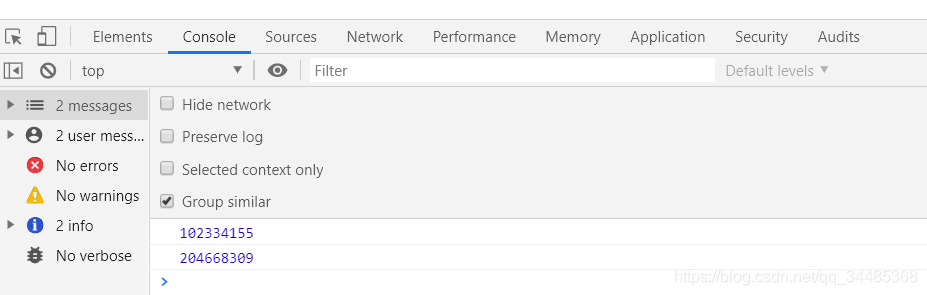
输出结果及优化详述

• 通过上图结果可以看到统计次数(count)值比数列值还要大
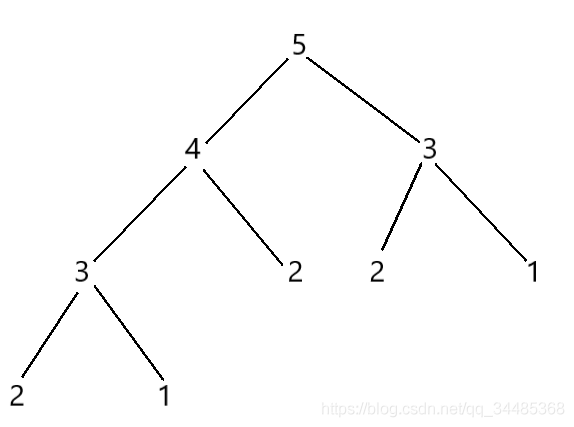
• 举个例子fibNumber(5)，递归求斐波那契数列第5项
• 计算第5项，需要先计算第4项和第3项的值
• 这样每个递归调用都触发了另外两个递归第4项和第3项的调用
• 而获得第4项和第3项的值又触发他们各自两个项的调用
• 一直到调用第1和2项结束这个规律
• 如下图，第1项，第2项，第3项都重复计算
• 也可以看到冗余计算的增长也是非常快速的

 

 

斐波那契数列优化递归函数

• 函数外定义一个对象P1保存斐波那契数列结果
• 函数中，先判断一下，P1对象中有没有保存过这一列的值
• 如果有，就直接取出数据返回就行了
• 如果没有，该怎么算怎么算
• 把算不出来的结果保存到对象中
• 再返回这个结果
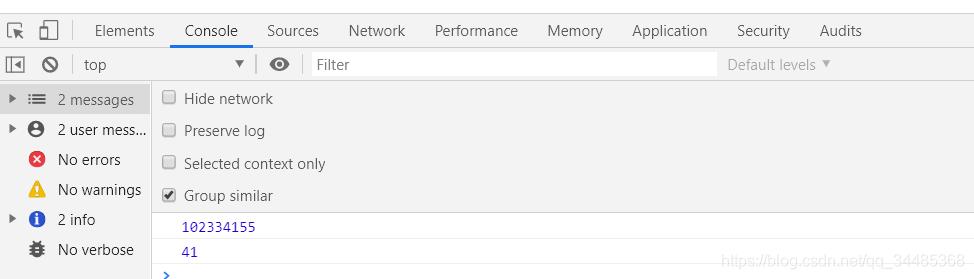
• 可以看到相比优化前的计算量，这个计算量还是大大的减少的

 
 //斐波那契数列优化

        let p1 = {}
        let count = 0

        function fibNumber(n) {
            if (p1[n]) {
                return p1[n]
            } else {
                count++
                if (n == 1 || n == 2)
                    return 1

                p1[n] = fibNumber(n - 1) + fibNumber(n - 2)
                return p1[n]
            }
        }
        console.log(fibNumber(40))
        console.log(count)

 

 

————————————————
版权声明：本文为CSDN博主「前端.木子李」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/qq_34485368/article/details/110096704