2024年牛客暑期多校训练营1 A题 A Bit Common题解 和 B-A Bit More Common题解
A题A Bit Common题目的大意:
- 首先,给你一个长度为n的序列A,A序列中每一个元素全都小于2m,并且大于等于0。
- A序列要满足存在一个非空子序列的与运算(&)和为1;
- 输出这样的A序列有几个,最后对正整数q取模。(1 <= n , m <=5000 , 1 <= q <=109)
- 输入只有一行n , m , q,输出包含一个整数。
题解:
要满足A序列的一个子序列 & 运算和为 1,则至少存在一个奇数。设A序列中存在k个整数,有n-k个偶数。
下图将每个数转换为2进制之后的 (m x k) 图 ,图中每一列都是一个数。
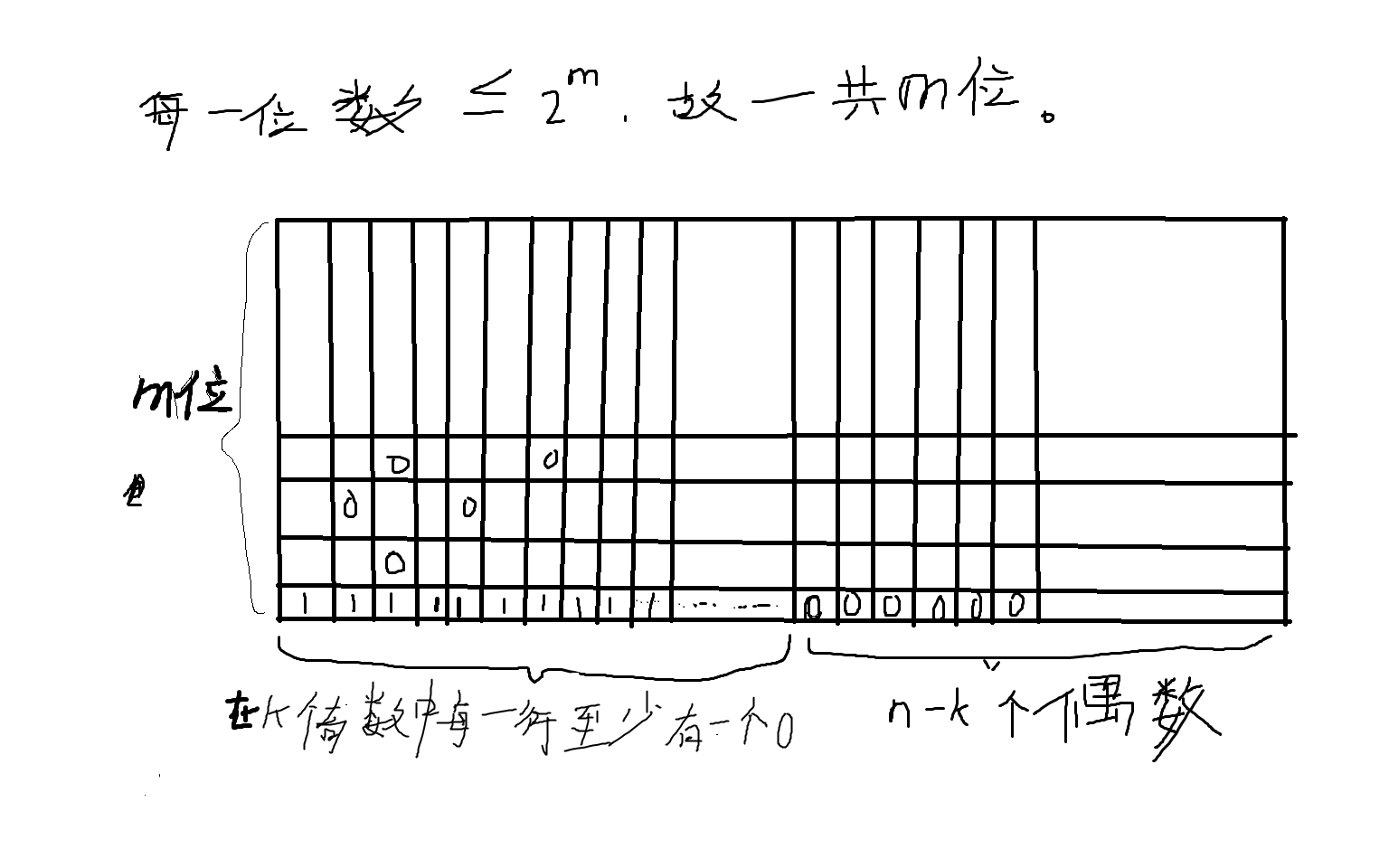
在这个图中每一行一共有2k种,去除全是1的情况(因为在取子序列时所有数全是奇数,要保证最后&和的结果是1,则每一行至少有一个0)有2k-1种,然后一共有m-1行,那么奇数总共有(2k-1)m-1种情况。
同理可得,偶数有2(n-k)(m-1)种情况。
又因为实际情况中奇数和偶数都是随机的,则总共有Ckn 2(n-k)(m-1) · (2k-1)m-1种情况。最后再从1到n进行累加得 ∑nk=1Ckn 2(n-k)(m-1) · (2k-1)m-1。
代码编写:
写代码的过程中主要有两个难点。一是求幂,因为k可以取到5000的,25000已经超过了long long的数据范围,我的解决方法是快速幂。二是求组合数,这里我采用了杨辉三角求组合数。
先讲一下快速幂。举个例子,求310,它可以变成95 。 这里5是奇数,我们将它变成 9 x 94,继续降低它的幂,变成9 x 812,最后变成 9 x (812)1。
在这个过程中,我们实际计算了(3*3)、(9*9)、(81*81)和 (9*812),我们需要计算10次,现在只需要计算4次,应用快速幂我们可以将O(n)的算法优化到O(logn)。
ll fast_POW(ll a ,ll b,ll c) //a是底数,b是指数,c是模 { ll ans=1; while(b) { if(b&1)//判断b是否为奇数
{ ans=(ans*a)%c; } a=(a*a)%c; b>>=1;//指数减小一倍 } return ans; }
然后再讲一下杨辉三角求组合数
首先Cnm=Cnm-1+Cn-1m-1,取第m个数时可以分两种考虑取或者不取,如果取则从剩下的m-1个数中取n-1个数,如果不取则从剩下的m-1个数中取n个数。
那么就可以通过递推公式dp[ i ][ j ]=dp[ i-1 ][ j ] + dp[ i-1 ][ j-1]。
| i \ j | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | .... |
| 0 | 1 | ||||||||
| 1 | 1 | 1 | |||||||
| 2 | 1 | 2 | 1 | ||||||
| 3 | 1 | 3 | 3 | 1 | |||||
| 4 | 1 | 4 | 6 | 4 | 1 | ||||
| 5 | 1 | 5 | 10 | 10 | 5 | 1 | |||
| 6 | 1 | 6 | 15 | 20 | 15 | 6 | 1 | ||
| 7 | 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 | |
| .... | 1 |
typedef long long ll; ll combination[5005][5005]; int q=1e9; for(int i=0;i<=5001;i++) { combination[i][0]=1; combination[i][i]=1; } for(int i=1;i<=5001;i++) { for(int j=1;j<=i;j++) { combination[i][j]=(combination[i-1][j]%q+combination[i-1][j-1]%q)%q;//为了防止最后的值超出限制,要进行取模。 } }
完整代码:
#include<bits/stdc++.h> using namespace std; typedef long long ll; ll combination[5005][5005]; ll fast_POW(ll a ,ll b,ll c)//算法时间复杂度为O(logN) { ll ans=1; while(b) { if(b&1){ ans=(ans*a)%c; } a=(a*a)%c; b>>=1; } return ans; } inline ll comb(ll n, ll m) { return combination[n][m]; } void solve(ll n ,ll m , ll q) { for(int i=0;i<=5001;i++) { combination[i][0]=1; combination[i][i]=1; } for(int i=1;i<=5001;i++)//递推算法时间复杂度为O(N2) { for(int j=1;j<=i;j++) { combination[i][j]=(combination[i-1][j] % q +combination[i-1][j-1] %q)%q;//一定要注意取模,每一个可能超出模q的运算都要取模,不然会非常折磨。 } } ll ans=0; for(int i=1;i<=n;i++) { ll ji=fast_POW(2, i ,q)-1; ans += comb(n , i) * fast_POW(ji,m-1,q) %q * fast_POW(fast_POW(2,n-i,q),m-1,q);//一定要注意取模,每一次可能超出模q的运算都要取模,很折磨。 ans=ans%q; } cout << ans; } signed main() { ll n,m,q; cin >> n >> m >> q; solve(n,m,q); return 0; }
B题A Bit More Common题目的大意:
- 首先,给你一个长度为n的序列A,A序列中每一个元素全都小于2m,并且大于等于0。
- A序列要满足存在两个非空子序列的与运算(&)和为1;
- 输出这样的A序列有几个,最后对正整数q取模。(1 <= n , m <=5000 , 1 <= q <=109)
- 输入只有一行n , m , q,输出包含一个整数。
题解:
这题在A题的基础上做了一些改动,将满足存在一个非空子序列的与运算(&)和为1改为存在两个非空子序列的与运算(&)和为1。那么只需要在A题的基础上减去有且仅有一个非空子序列的(&)运算和为1的情况即可。现在考虑什 么情况下,一个序列有且仅有一个非空子序列。当删去满足该条件的子序列中任意一个数之后,该子序列都不再满足(&)运算和为1。现画图如下:
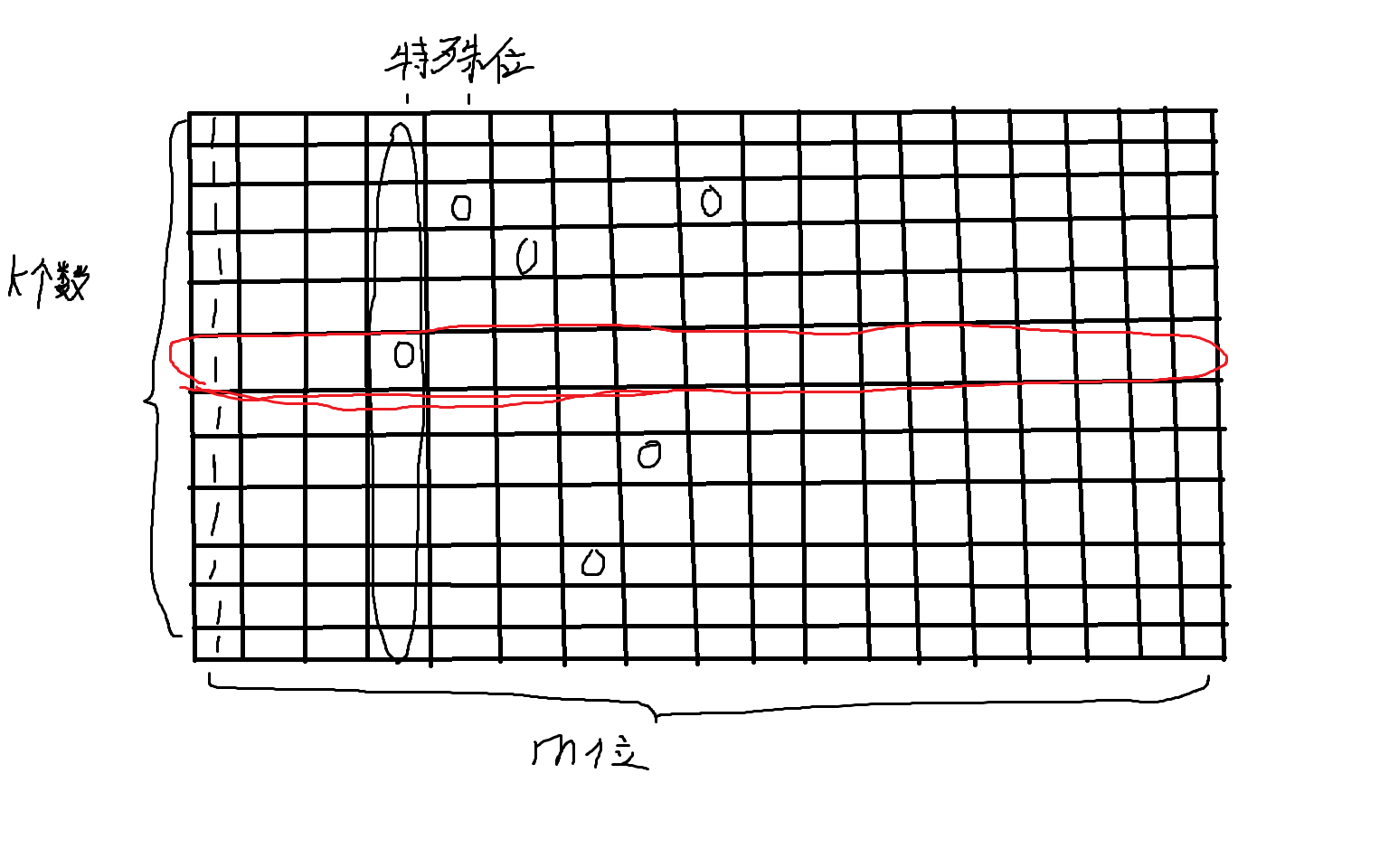
我们将一列中只有一个0的位叫特殊位。当我们删除画红圈的哪一行时,由于特殊位中只存在一个0,该特殊为(&)和势必为1。为了构造删除任意一个数都不能使它的(&)和为1,k个数要满足的条件为每个数都至少要有一个特殊 位。那么我们该如何解决这个问题呢?我们可以将其抽象为把j个特殊位分给i个数,这个问题的思考方式与第二类斯特林数的思考方式相类似,唯一不同是这个问题中,i个数都是有区别的。
现在我们来建立递推公式dp[ i ][ j ]的意思为把j个特殊位分给i个数,dp[ i ][ j ]可以由两种情况递推而来。第一种,j-1个特殊位分给了i个数,i个数中每个数都至少存在了一个特殊位,那么第j个特殊位可以分给i个数中的任意一 个,有i种情况,结果为i*dp[ i ][ j-1 ];第二种,j-1个特殊位分给了i-1个数,则第j个特殊位必须单独分给第i个数,而第i个数又可以是i个数中任意一个,于是也有i种情况。
综上所述,我们可以写出递推公式dp[i][j]=i * ( dp[i][j-1] + dp[i-1][j-1])。
我们假设有t个特殊位要分给k个数(k <= t <= m-1),也就是dp[ k ][ t ],后面(m-1-t)位要去掉全是1和只存在一个0的情况,有(2k-k-1)m-1-t种情况。
最后我们得到答案Ckn 2(n-k)(m-1) ∑m-1t=k Ctm-1dp[ k ][ t ] * (2k-k-1)m-1-t )。
代码编写:
#include<bits/stdc++.h> using namespace std; typedef long long ll; ll combination[5005][5005],dp[5005][5005]; ll fast_POW(ll a ,ll b,ll c) { ll ans=1; while(b) { if(b&1){ ans=(ans*a)%c; } a=(a*a)%c; b>>=1; } return ans; } inline ll comb(ll n, ll m) { return combination[n][m]; } void solve(ll n ,ll m , ll q) { for(int i=0;i<=5001;i++) { combination[i][0]=1; combination[i][i]=1; } for(int i=1;i<=5001;i++) { for(int j=1;j<=i;j++) { combination[i][j]=(combination[i-1][j] % q +combination[i-1][j-1] %q)%q; } } for(int j=1;j<=5001;j++) { dp[1][j]=1; } for(int i=2;i<=5001;i++) { for(int j=i;j<=5001;j++) { dp[i][j]=i * ( (dp[i][j-1] + dp[i-1][j-1]) %q )%q; } } ll ans=0; for(int i=1;i<=n;i++) { ll ji=fast_POW(2, i ,q)-1; ans = (ans+comb(n , i) * fast_POW(ji,m-1,q) %q * fast_POW(fast_POW(2,n-i,q),m-1,q)%q)%q; } ll ans1=n * fast_POW(2,(n-1)*(m-1),q) %q; for(int i=2;i<=n;i++) { ll od=1,oddi=comb(n,i) * fast_POW(2,(n-i)*(m-1),q) % q; ll os=fast_POW(2,i,q)-i-1; for(int j=m-1;j>=i;j--) { ans1+=oddi*comb(m-1,j)%q * dp[i][j] %q * od %q;//这里我是曾经用fast_POW(fast_POW(...)....)这样的形式来写,但不知为何判断题目时运行超时了。我推测是因为算法时间复杂度最大只能到O(n2),再大就无法接受了。 ans1=ans1%q; od=od*os%q; } } cout << (ans-ans1+q)%q; } signed main() { ll n,m,q; cin >> n >> m >> q; solve(n,m,q); return 0; }
posted on 2024-07-19 16:14 kiyotaka-ayanokoji 阅读(40) 评论(0) 编辑 收藏 举报



