Queue和Priority Queue源码解读
Queue
Queuedocs: https://docs.oracle.com/en/java/javase/12/docs/api/java.base/java/util/Queue.html
LinkedListdocs: https://docs.oracle.com/en/java/javase/12/docs/api/java.base/java/util/LinkedList.htmlversion: java12
在Java中,Queue是一个抽象的接口,定义了队列(特性:FIFO)最基本的操作,在其之下,又分别了定义其它的接口继承了Queue:
- BlockingQueue
:阻塞队列 - BlockingDeque
:继承了 BlockingQueue,是阻塞的双端队列 - Deque
:双端队列 - TransferQueue
:继承了 BlockingDeque,在其基础上又增加了保证生产者阻塞直到元素被某个线程消费的行为,具体实现查看LinkedTransferQueue
以上的BlockingQueue、BlockingDeque、TransferQueue用于多线程,这里不过多介绍。我们主要看Deque的实现LinkedList,并以实现Queue的视角描述。
Queue
Queue定义了几个基本操作如下:
| 会抛出异常 | 返回特殊值(一般为null) | |
|---|---|---|
| 插入 | add(e) | offer(e) |
| 删除 | remove() | poll() |
| 取出元素 | element() | peek() |
当然,Java内常用的链表数据结构LinkedList是实现了Deque接口。Deque接口是在Queue的基础上又扩展了一些函数。
| 会抛出异常 | 返回特殊值(一般为null) | |
|---|---|---|
| 插入头 | addFirst(e) | offerFirst(e) |
| 插入尾 | addLast(e) | offerLast(e) |
| 删除头 | removeFirst() | pollFirst() |
| 删除尾 | removeLast() | pollLast() |
| 取出头 | elementFirst() | peekFirst() |
| 取出尾 | elementLast() | peekLast() |
Deque的操作定义除了有FIFO的特性之外,它也具备栈的特征——LIFO。
栈方法(Stack) |
等效的Deque方法 |
|---|---|
| push(e) | addFirst(e) |
| pop() | removeFirst() |
| peek() | getFirst() |
LinkedList
对LinkedList这样的实现来说,首先要定义出大致的结构:
public class LinkedList<E>
extends AbstractSequentialList<E>
implements List<E>, Deque<E>, Cloneable, java.io.Serializable
{
transient int size = 0;
/**
* Pointer to first node.
* Invariant: (first == null && last == null) ||
* (first.prev == null && first.item != null)
*/
transient Node<E> first;
/**
* Pointer to last node.
* Invariant: (first == null && last == null) ||
* (last.next == null && last.item != null)
*/
transient Node<E> last;
private static class Node<E> {
E item;
Node<E> next;
Node<E> prev;
Node(Node<E> prev, E element, Node<E> next) {
this.item = element;
this.next = next;
this.prev = prev;
}
}
}
对LinkedList的数据结构来说,它定义了first和last两个首尾指针,指向它首尾位置的元素。其中Node是每个元素在这个数据结构中的定义,除了本身的内容之外,还定义了prev、next指向前后两个节点。
add() 、offer()
不论是add()、addLast()方法,最终都是使用的linkLast()方法。
其实现就是取出last节点,实例化一个新的Node,设置新节点的prev,并将新的节点设置为当前新的last节点。
public class LinkedList<E>{
/**
* Links e as last element.
*/
void linkLast(E e) {
final Node<E> l = last;
final Node<E> newNode = new Node<>(l, e, null);
last = newNode;
if (l == null)
first = newNode;
else
l.next = newNode;
size++;
modCount++;
}
}
remove()、poll()
remove()和poll()真实实现都在unlinkFirst()方法中。
本质上就是取出第一个元素,置空next,再取出第二个元素,将第二个元素的prev置空,这样就完成了头元素的删除操作。
public class LinkedList<E>{
public E removeFirst() {
final Node<E> f = first;
if (f == null)
throw new NoSuchElementException();
return unlinkFirst(f);
}
/**
* Unlinks non-null first node f.
*/
private E unlinkFirst(Node<E> f) {
// assert f == first && f != null;
final E element = f.item;
final Node<E> next = f.next;
f.item = null;
f.next = null; // help GC
first = next;
if (next == null)
last = null;
else
next.prev = null;
size--;
modCount++;
return element;
}
}
element()、peek()
element()和peek()都是直接返回LinkedList定义的first元素,无非判定抛异常或者返回null而已。
这里不多赘述。
PriorityQueue
docs: https://docs.oracle.com/en/java/javase/12/docs/api/java.base/java/util/PriorityQueue.html
version: java12
PriorityQueue也是Queue的一个具体实现,是基于优先级堆的无界优先队列,其功能主要是实现了元素的有序性。如果想要使用线程安全的优先队列,则应该使用PriorityBlockingQueue。
PriorityQueue的排序是自然顺序排序或者是实现Comparator,这取决于构造的时候用哪个构造函数,插入的元素不能为空,不能不可比较。
PriorityQueue Define
public class PriorityQueue<E> extends AbstractQueue<E>
implements java.io.Serializable {
private static final int DEFAULT_INITIAL_CAPACITY = 11;
/**
* Priority queue represented as a balanced binary heap: the two
* children of queue[n] are queue[2*n+1] and queue[2*(n+1)]. The
* priority queue is ordered by comparator, or by the elements'
* natural ordering, if comparator is null: For each node n in the
* heap and each descendant d of n, n <= d. The element with the
* lowest value is in queue[0], assuming the queue is nonempty.
*/
transient Object[] queue; // non-private to simplify nested class access
/**
* The number of elements in the priority queue.
*/
private int size = 0;
/**
* The comparator, or null if priority queue uses elements'
* natural ordering.
*/
private final Comparator<? super E> comparator;
/**
* The number of times this priority queue has been
* <i>structurally modified</i>. See AbstractList for gory details.
*/
transient int modCount = 0;
}
PriorityQueue底层是一个数组作为容器,初始容量为11。
那为什么是数组呢?
这源自于PriorityQueue数据结构的设计是二叉小顶堆,而它正好可以通过数组表示。
假如定义的数组数据如下:
Character[] queue = new Character[]{'a','b','C','D','E','F','G'};
那么数组下标为零的元素就在堆顶,此时堆顶元素为'a',那么'a'左边的元素就是'b','a'右边的元素就是'C','b'的左边元素为'D',右边元素为'E',以此类推,最终构成了小顶堆的结构。
如下图所示:
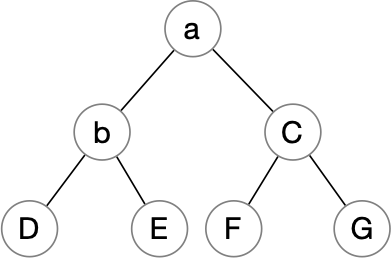
我们基本可以得出几个通用的公式:
公式1:父节点在数组中的下标 = (当前节点下标值 - 1) / 2
公式2:左节点的下标 = 当前节点下标值*2 + 1
公式3:右节点的下标 = 当前节点下标值*2 + 2
这几个公式会在PriorityQueue中使用。
offer()
我们先来看下插入元素。
public class PriorityQueue<E>{
/**
* Inserts the specified element into this priority queue.
*
* @return {@code true}
*/
public boolean offer(E e) {
if (e == null)
throw new NullPointerException();
modCount++;
int i = size;
if (i >= queue.length)
grow(i + 1); //扩容
size = i + 1;
if (i == 0)
queue[0] = e;
else
siftUp(i, e);
return true;
}
/**
* Inserts item x at position k, maintaining heap invariant by
* promoting x up the tree until it is greater than or equal to
* its parent, or is the root.
*
* To simplify and speed up coercions and comparisons. the
* Comparable and Comparator versions are separated into different
* methods that are otherwise identical. (Similarly for siftDown.)
*
* @param k the position to fill
* @param x the item to insert
*/
private void siftUp(int k, E x) {
if (comparator != null)
siftUpUsingComparator(k, x);
else
siftUpComparable(k, x);
}
private void siftUpUsingComparator(int k, E x) {
while (k > 0) {
int parent = (k - 1) >>> 1;
Object e = queue[parent];
if (comparator.compare(x, (E) e) >= 0)
break;
queue[k] = e;
k = parent;
}
queue[k] = x;
}
private void siftUpComparable(int k, E x) {
Comparable<? super E> key = (Comparable<? super E>) x;
while (k > 0) {
int parent = (k - 1) >>> 1;
Object e = queue[parent];
if (key.compareTo((E) e) >= 0)
break;
queue[k] = e;
k = parent;
}
queue[k] = key;
}
}
在offer()方法进来时,判断数组长度是否容量不足,容量不足则通过grow()方法扩容:
private void grow(int minCapacity) {
int oldCapacity = queue.length;
// Double size if small; else grow by 50%
int newCapacity = oldCapacity + ((oldCapacity < 64) ?
(oldCapacity + 2) :
(oldCapacity >> 1));
// overflow-conscious code
if (newCapacity - MAX_ARRAY_SIZE > 0)
newCapacity = hugeCapacity(minCapacity);
queue = Arrays.copyOf(queue, newCapacity);
}
当前数组容量小于64,则新的容量为原来的容量+2;当前数组容量大于64,则新的容量为原来的容量基础上再增加50%,最大不能超过Int的最大值。
核心方法是siftUp()方法,非空队列每次新增元素都需要重新调整堆。
我们以siftUpUsingComparator()方法为例:
int parent = (k - 1) >>> 1;其实就是使用公式1计算parent的值;- 第一次循环最后一个值与父节点比较,如果是最大值,则不用动,否则这两个元素位置置换;
- 继续循环,直到跳出循环,或者到堆顶;
peek()
获取元素就比较简单,获取最小值的那个元素,本质上就是获取数组的最小值。


