LeetCode-897-递增顺序搜索树

LeetCode-897-递增顺序搜索树

题目

给你一棵二叉搜索树，请你 按中序遍历 将其重新排列为一棵递增顺序搜索树，使树中最左边的节点成为树的根节点，并且每个节点没有左子节点，只有一个右子节点。

示例 1：

输入：root = [5,3,6,2,4,null,8,1,null,null,null,7,9]
输出：[1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]
示例 2：

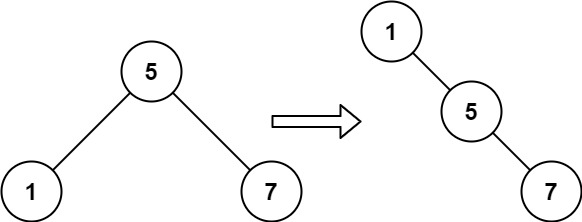
输入：root = [5,1,7]
输出：[1,null,5,null,7]

提示：

树中节点数的取值范围是 [1, 100]
0 <= Node.val <= 1000

思路

如果按照题意，直接中序遍历构造一个新的二叉树，思路上相对简单，但是时间和空间复杂度较高

因此可以在中序遍历二叉树时，改变此二叉树的形状，使其符合题意。

根据观察，需求的二叉树左子树为空，右子树大于根节点，而BST的特点是左子树小于根节点，右子树大于根节点

因此可以将BST中每个节点的左子树变为父节点，然后左子树置为空即可，代码如下所示。

最后的结果时间0ms，空间6M。感觉只用了两个指针变量，不知道为啥会消耗这么多空间，可能算上了二叉树的大小。

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
struct TreeNode* increasingBST(struct TreeNode* root){
    if (!root) return NULL;
    struct TreeNode* leftRootNode = root;
    if (root->left) {
        // 将左子树变成父节点
        leftRootNode = increasingBST(root->left);
        struct TreeNode* leftRightNode = root->left;
        while (leftRightNode->right) leftRightNode = leftRightNode->right;
        //printf("%d %d\n", leftRightNode->val, node->val);
        leftRightNode->right = root;
        root->left = NULL;
    }
    if (root->right) {
        // 改变右子树为右子树的返回值
        root->right = increasingBST(root->right);
    }
    // 若节点没有左子树，返回值为当前节点，若有，返回值为左子树的根节点
    return leftRootNode;
}