机器学习:L1和L2正则化项的理解
正则化(Regularization)
机器学习中几乎都可以看到损失函数后面会添加一个额外项,常用的额外项一般有两种,称作L1正则化 和 L2正则化,或者 L1范数 和 L2范数。
L1正则化和L2正则化可以看做是损失函数的惩罚项。所谓“惩罚”是指对损失函数中的某些参数做一些限制。对于线性回归模型,使用L1正则化的模型建叫做Lasso回归,使用L2正则化的模型叫做Ridge回归(岭回归)。
L1正则化和L2正则化的说明如下:
- L1正则化是指权值向量w中各个元素的绝对值之和,通常表示为∣∣w∣∣1
- L2正则化是指权值向量w中各个元素的平方和然后再求平方根(Ridge回归的L2正则化项有平方符号),通常表示为∣∣w∣∣2
一般都会在正则化项之前添加一个系数,用α表示或用λ表示。这个系数需要用户指定。
那添加L1和L2正则化有什么用?下面是L1正则化和L2正则化的作用,这些表述可以在很多文章中找到。
- L1正则化可以产生稀疏权值矩阵,即产生一个稀疏模型,可以用于特征选择
- L2正则化可以防止模型过拟合(overfitting);一定程度上,L1也可以防止过拟合
稀疏模型与特征选择的关系
上面提到L1正则化有助于生成一个稀疏权值矩阵,进而可以用于特征选择。为什么要生成一个稀疏矩阵?
稀疏矩阵指的是很多元素为0,只有少数元素是非零值的矩阵,即得到的线性回归模型的大部分系数都是0. 通常机器学习中特征数量很多,例如文本处理时,如果将一个词组(term)作为一个特征,那么特征数量会达到上万个(bigram)。在预测或分类时,那么多特征显然难以选择,但是如果代入这些特征得到的模型是一个稀疏模型,表示只有少数特征对这个模型有贡献,绝大部分特征是没有贡献的,或者贡献微小(因为它们前面的系数是0或者是很小的值,即使去掉对模型也没有什么影响),此时我们就可以只关注系数是非零值的特征。这就是稀疏模型与特征选择的关系。
L1和L2正则化的直观理解
这部分内容将解释为什么L1正则化可以产生稀疏模型(L1是怎么让系数等于零的),以及为什么L2正则化可以防止过拟合。
正则化和特征选择的关系
假设有如下带L1正则化的损失函数:
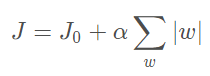
其中J0是原始的损失函数,加号后面的一项是L1正则化项,α是正则化系数。注意到L1正则化是权值的绝对值之和,J是带有绝对值符号的函数,因此J是不完全可微的。机器学习的任务就是要通过一些方法(比如梯度下降)求出损失函数的最小值。当我们在原始损失函数J0后添加L1正则化项时,相当于对J0做了一个约束。令L=α∑∣w∣,则J=J0+L 。此时我们的任务变成在L约束下求出J0取最小值的解。考虑二维的情况,即只有两个权值w1和w2,此时L=∣w1∣+∣w2∣。对于梯度下降法,求解J0的过程可以画出等值线,同时L1正则化的函数L也可以在w1w2的二维平面上画出来。如下图:
图中等值线是J0的等值线,黑色方形是L函数的图形。L=∣w1∣+∣w2∣,这个函数画出来就是一个方框(可以自己动手画一下)。
在图中,当J0等值线与L图形首次相交的地方就是最优解。上图中J0与在L的一个顶点处相交,这个顶点就是最优解。注意到这个顶点的值是(w1,w2)=(0,w)可以直观想象,因为L函数有很多“突出的角”(二维情况下四个,多维情况下更多),J0与这些角接触的机率会远大于与L其它部位接触的机率(这是很直觉的想象,突出的角比直线的边离等值线更近些),而在这些角上,会有很多权值等于0(因为角就在坐标轴上),这就是为什么L1正则化可以产生稀疏模型,进而可以用于特征选择。
而正则化前面的系数α,可以控制L图形的大小。α越小,L的图形越大(上图中的黑色方框);α越大,L的图形就越小,可以小到黑色方框只超出原点范围一点点,这是最优点的值(w1,w2)=(0,w)中的w可以取到很小的值。
类似地,假设有如下带L2正则化的损失函数:
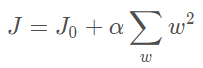
同样可以画出在二维平面上的图形,如下:
二维平面下L2正则化的函数图形是个圆(绝对值的平方和,是个圆),与方形相比,被磨去了棱角。因此J0与L相交时使得w1
或w2等于零的机率小了许多(这个也是一个很直观的想象),这就是为什么L2正则化不具有稀疏性的原因,因为不太可能出现多数w都为0的情况。
为什么梯度下降的等值线与正则化函数第一次交点是最优解?
这是带约束的最优化问题。这应该是在大一的高等数学就学到知识点,因为这里要用到拉格朗日乘子。如果有这样的问题,就需要复习一下高等数学了。这里有一个比较详细的数学讲解,可以参考:带约束的最优化问题。
L2正则化和过拟合的关系
拟合过程中通常都倾向于让权值尽可能小,最后构造一个所有参数都比较小的模型。因为一般认为参数值小的模型比较简单,能适应不同的数据集,也在一定程度上避免了过拟合现象。可以设想一下对于一个线性回归方程,若参数很大,那么只要数据偏移一点点,就会对结果造成很大的影响;但如果参数足够小,数据偏移得多一点也不会对结果造成什么影响,专业一点的说法是“抗扰动能力强”。
那为什么L2正则化可以获得值很小的参数?
以线性回归中的梯度下降法为例,假设要求解的参数为θ,而hθ(x)是我们的假设函数。线性回归一般使用平方差损失函数。单个样本的平方差是(hθ(x)−y)2,如果考虑所有样本,损失函数是对每个样本的平方差求和,假设有m个样本,线性回归的代价函数如下,为了后续处理方便,乘以一个常数1/2m:
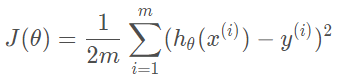
在梯度下降算法中,需要先对参数求导,得到梯度。梯度本身是上升最快的方向,为了让损失尽可能小,沿梯度的负方向更新参数即可。
对于单个样本,先对某个参数θj求导:
![]()
注意到hθ(x)的表达式是 hθ(x)=θ0x0+θ1x1+⋯+θnxn. 单个样本对某个参数θj求导,∂/∂θj(hθ(x))=xj.
最终上式结果如下:
![]()
在考虑所有样本的情况,将每个样本对θj的导数求和即可,得到下式:
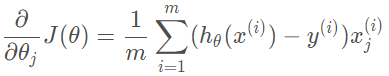
梯度下降算法中,为了尽快收敛,会沿梯度的负方向更新参数,因此在(3.3)式前添加一个负号,并乘以一个系数α\alphaα(即学习率),得到最终用于迭代计算参数θj的形式:
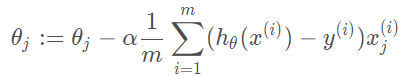
其中α是学习率(learning rate)。 上式是没有添加L2正则化项的迭代公式,如果在原始代价函数之后添加L2正则化,则迭代公式会变成下面的样子:
![]()
其中λ就是正则化参数。从上式可以看到,与未添加L2正则化的迭代公式相比,每一次迭代,θj都要先乘以一个小于1的因子(即(1−αλm),从而使得θj不断减小,因此总的来看,θ是不断减小的。
最开始也提到L1正则化一定程度上也可以防止过拟合。之前做了解释,当L1的正则化系数很小时,得到的最优解会很小,可以达到和L2正则化类似的效果。
正则化参数的选择
L1正则化参数
通常越大的λ可以让代价函数在参数为0时取到最小值。因为正则化系数越大,正则化的函数图形(上文图中的方形或圆形)会向坐标轴原点收缩得越厉害,这个现象称为shrinkage,过程可以称为shrink to zero. 下面是一个简单的例子,这个例子来自Quora上的问答。为了方便叙述,一些符号跟这篇帖子的符号保持一致。
假设有如下带L1正则化项的代价函数:
![]()
其中x是要估计的参数,相当于上文中提到的w以及θ。 这个例子中的正则化函数L就是L=λ∣x∣。注意到L1正则化在某些位置是不可导的,当λ足够大时可以使得F(x)在x=0时取到最小值。如下图:
作为一个直观的例子,这个图的示例中,取了f(x) = (x-1)^2作为损失函数,其实可以取更复杂的,但不好画图,不过原理是一样的,因为损失函数都是凸函数,很多性质是一样的。
正则化分别取λ=0.5和λ=2,可以看到越大的λ越容易使F(x)在x=0时取到最小值。
此外也可以自己计算一下,当损失函数f(x)和正则化函数L=∣x∣在定义域内第一次相交的地方,就是整个代价函数F(x)的最优解。
L2正则化参数
从公式
![]()
可以看到,λ越大,θj衰减得越快。另一个理解可以参考 图 “L2正则化”,λ越大,L2圆的半径越小,最后求得代价函数最值时各参数也会变得很小,同样是一个shrink to zero的过程,原理与L1正则化类似。


