深度学习：梯度下降法数学表示式的详细推导

很多深度学习的书籍以及网上介绍深度学习的相关文章里面介绍了梯度法求损失函数最优化，但很少会解释梯度法的数学式是怎么得出来的，经过一番数学推理和文献查找（其实Ian Goodfellow等著的《深度学习》也没有通俗解释，用了晦涩的语言和符号表示，没有具体说明，参见其第四章第三节），做此笔记。

 

梯度

通俗来说，梯度就是表示某一函数在该点处的方向导数沿着该方向取得较大值，即函数在当前位置的导数。很多资料都以下山的例子来类比梯度下降法。这里，用θo是自变量参数，即下山位置坐标，η是学习因子，即下山每次前进的一小步（步进长度），θ是更新后的θo，即下山移动一小步之后的位置。则

                                                                    

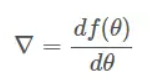
上式中，θ是自变量，f(θ)是关于θ的函数，表示梯度。
如果函数f(θ)是凸函数，那么就可以使用梯度下降算法进行优化。梯度下降算法的公式我们已经很熟悉了：

                                                            

 

一阶泰勒展开式

这里需要一点数学基础，对泰勒展开式有些了解。简单地来说，一阶泰勒展开式利用的就是函数的局部线性近似这个概念。这里需要用到一阶泰勒展开式：

                                                  

或者不理解泰勒展开则结合导数的近似意义：          y ≈ y0 + (x+△ x)*y'

                               

 

 

余弦变化规律

 A和B均为向量，α为两个向量之间的夹角。A和B的乘积为：

                                                   

（ 注：  || ||就是取绝对值 |  | ）  

||A|| 和 ||B|| 均为标量，在||A|| 和 ||B|| 确定的情况下，只要cos(α) = -1，即A和B完全反向，就能让A和B的向量乘积最小(负的最大值)。

 

 

梯度下降数学原理

知道了一阶泰勒展开式之后，接下来就是重点。我们来看一下梯度下降算法是如何推导的。

                                        

其中，θ-θo是微小矢量，它的大小就是我们之前讲的步进长度η，类比于下山过程中每次前进的一小步，η为标量，而θ-θo的单位向量用v表示。则θ-θo可表示为： 

                                                        

特别需要注意的是，θ-θo不能太大，因为太大的话，线性近似就不够准确，一阶泰勒近似也不成立了。替换之后，f(θ)的表达式为: 

                                            

重点来了，局部下降的目的是希望每次θ更新，都能让函数值f(θ)变小。也就是说，上式中，我们希望f(θ)<f(θo)。则有: 

                                            

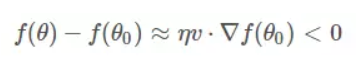
因为η为标量，且一般设定为正值，所以可以忽略，不等式变成了： 

                                                           

上面这个不等式非常重要。v和都是向量，是当前位置的梯度方向，v表示下一步前进的单位向量，是需要我们求解的，有了它，就能根据θ-θo=ηv确定θ值了。

 

由余弦变化规律，当v和互为反向，即v为当前梯度方向的负方向的时候，能让最大程度地小，也就保证了v的方向是局部下降最快的方向。    

知道v是的反方向后,可直接得到:

                                                         

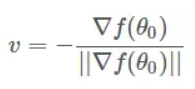
之所以要除以的模，是因为v是单位向量。

求出最优解v之后，带入到θ-θo=ηv中，得： 

                                                        

 

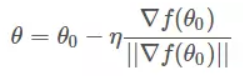
一般地,因为是标量，可以并入到步进因子η中，即简化为

                                                         

 

 

综上，通过一阶泰勒展开式，利用线性近似和向量相乘最小化的思想证明了梯度下降算法的数学原理。也许有读者之前很熟悉梯度下降算法，但也许对它的推导过程并不清楚。