11/06信竞快乐模拟赛
第一题 melon
题目描述
【时间限制】1000MS 【空间限制】65536KB
【输入文件】melon.in 【输出文件】melon.out
【题目描述】
Todobe和Yahsem66比赛吃瓜。
桌上一共有n块瓜,他们可以从桌上拿走不多于k块瓜来吃,吃一块瓜需要1分钟的时间,只有吃完手里的所有瓜之后才可以再去拿瓜,拿瓜的时间不计。如果两人在同一时间点拿瓜,Yashem66会发扬谦让精神让Todobe先拿,开始比赛时也是Todobe先拿。
举个例子,如果n=10,k=4,Todobe先拿走3块,Yashem66拿走2块,Yashem66吃完之后Todobe还有1块没有吃完。Yashem66再拿走4块,然后Todobe就只能再吃到1块,最终Todobe吃了4块,而Yashem66吃了6块。
两个人都想尽可能吃更多的瓜,贪吃的Todobe想知道她最多能吃到多少块瓜。
【输入】
输入包括一行两个整数,n、k。
【输出】
输出一行一个整数,代表Todobe最多能吃到多少块瓜。
【样例输入1】
2 1
【样例输出1】
1
【样例输入2】
10 4
【样例输出2】
5
【数据范围与约定】
对于0%的数据,与样例相同;
对于10%的数据,n<=2*k;
对于另30%的数据,k=2;
对于100%的数据,n,k<=100000。
思路
考试的时候直接通过样例和自己造的几组简单规律得出了规律,但有部分错误:
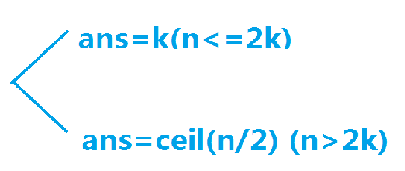
问题在于n<=2k时,k不一定一定小于n,则需要k op n
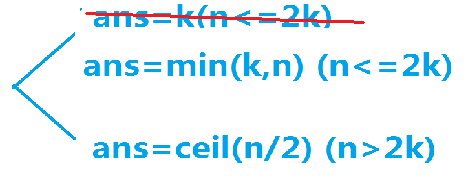
分析过程(网上找的)
n<=k直接是n,k<n<=2k就是k
当n>2k时,考虑一次只吃一个瓜,这样就有更大决策空间
当剩余瓜数<=2*k时#接选k个
所以答案为ceil(n/2)
代码
#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
const int maxn=100005;
int ans;
int main(){
freopen("melon.in","r",stdin);
freopen("melon.out","w",stdout);
int n,k;scanf("%d%d",&n,&k);
if(n<=2*k) ans=min(n,k);
else ans=(n+1)>>1;
printf("%d",ans);
return 0;
}
第二题 melon
题目描述
【时间限制】2000MS 【空间限制】524288KB
【输入文件】change.in 【输出文件】change.out
【题目描述】
Todobe开了一家店,Yashem66连续n天都会光顾这家店。
Yashem66只有100元的纸币和1元的硬币,他知道Todobe懒的一批,很讨厌找零这件事情,每天Todobe都会有一个心情值wi,如果Todobe第i天需要找零,那她的不愉悦度就会增加wi*找零的钱数。当Todobe需要找零时,她也会找给Yashem66若干1元硬币,但她不会找给Yashem66 100个及以上的硬币。
假设Yashem66一开始有足够的纸币和m个硬币,他在第i天,会买价值ci元的产品。他想尽可能降低Todobe的不愉悦度,请你告诉他Todobe 的不愉悦度最少是多少。
【输入】
第一行两个整数n、m。
第二行有n个整数,第i个整数代表ci,第i天Yashem66购买的价格。
第三行有n个整数,第i个整数代表wi,第i天Todobe的心情值。
【输出】
输出一行一个整数代表Todobe不愉悦度的最小值。
【样例输入1】
5 42
117 71 150 243 200
1 1 1 1 1
【样例输出1】
79
【样例解释1】
第一天花费1张100元纸币和17个1元硬币,剩余25个硬币,不愉悦度为0;
第二天花费1张100元纸币,找零29,剩余54个硬币,不愉悦度为29;
第三天花费2张100元纸币,找零50,剩余104个硬币,不愉悦度为79;
第四天花费2张100元纸币和43个1元硬币,剩余61个硬币,不愉悦度为79;
第五天花费2张100元纸币,不愉悦度为79.
【样例输入2】
5 42
117 71 150 243 200
5 4 3 2 1
【样例输出2】
230
【样例解释2】
第一天花费1张100元纸币和17个1元硬币,剩余25个硬币,不愉悦度为0;
第二天花费1张100元纸币,找零29,剩余54个硬币,不愉悦度为116;
第三天花费1张100元纸币和50个1元硬币,剩余4个硬币,不愉悦度为116;
第四天花费3张100元纸币,找零57,剩余61个硬币,不愉悦度为230;
第五天花费2张100元纸币,不愉悦度为230.
【数据范围与约定】
对于0%的数据与样例相同;
对于20%的数据,n<=20;
对于另20%的数据,ci=1;
对于100%的数据,n<=105,m<=109,1<=ai,ci<=10^5。
思路
考试的时候用的暴力回溯,20分。
正解:
贪心,贪每一步都让找零的时候最小的不快乐值,每次硬币不够的时候就取不快乐值最小的那次的硬币。
以下的“钱”都指需要付的硬币数量,并令当前硬币量为coin
考虑每一步:
将需要找零时的不快乐指数存在一个堆中
因为不管钱够还是不够都需要付这部分钱:
则coin-=c[i];
如果coin<0
则取不快乐指数最小的取出并加上。
现在的硬币数量为coin+100
(因为找零的数量为:100-c[i])
代码
#include <cstdio>
#include <iostream>
#include <queue>
using namespace std;
const int maxn=1e5+5;
int n,m;
long long ans=0;
priority_queue<intq;//将不快乐指数升序排
int c[maxn],w[maxn];//价格(需要付的硬币数量) 心情
void init(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%d",&c[i]);
c[i]%=100;
}
for(int i=1;i<=n;i++) scanf("%d",&w[i]);
}
int main(){
freopen("change.in","r",stdin);
freopen("change.out","w",stdout);
init();
for(int i=1;i<=n;i++){
if(c[i]%100==0) continue;
int unhappy=w[i]*(100-c[i]);//因为默认降序
q.push(-unhappy);
m-=c[i];
if(m<0){
int x=-q.top();q.pop();
ans+=x;
m+=100;
}
}
printf("%lld",ans);
return 0;
}
第三题 tree
题目描述
Fanvree 很聪明,解决难题时他总会把问题简单化。 例如,他就整天喜欢把图转化为树。但是他不会缩环,那他怎么转化呢? 这是一个有 n 个点 m 条双向边的图,Fanvree 会选定一个节点,然后删掉这个节点和这个点连出去的边, 如果变成了一棵树,那么这个节点便是可行的,什么是树呢?树也即无简单环的无向连通图。 告诉 Fanvree 可能的节点是什么。
输入:
第一行两个正整数 n 和 m,表示有 n 个点 m 条边,保证 n≥2。 接下来 m 行,每行两个整数 v,u,表示 v 和 u 之间有一条无向边 1≤v,u≤n,保证没 有重边和自环。
输出:
第一行一个正整数 ns,表示这个图中有 ns 个结点可选。 接下来一行,共 ns 个整数,每个整数表示一个可选结点的编号。 请按编号从小到大的顺序输出。 数据保证图中至少存在一个可选的结点。
样例输入:
6 6
1 2
1 3
2 4
2 5
4 6
5 6
样例输出:
3
4 5 6
数据范围:
对于 40%的数据:n,m<=1000;
另外存在 10%的数据:m=n-1;
思路
考试的时候用的暴力+bfs,即枚举每个被删除的点,再用bfs检查是否为树和连通图(当然检查是否是树的时候用的father数组胡乱做的)
正解:
很简单的一道图论题。
根据题意:
删除一个点形成树必须满足的条件:
1、删除这条点后有顶点-1条边
2、删除点后依旧为连通图(即非割点)
重点就是求割点的Tarjan
代码
#include <cstdio>
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
const int maxn=100005;
int n,m,root=1;
vector<int> g[maxn];
bool cutpoint[maxn];
int dfn[maxn],low[maxn],t;
int edge[maxn],ans[maxn],newp=0;
void init(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++){
int u,v;scanf("%d%d",&u,&v);
g[u].push_back(v);
g[v].push_back(u);
edge[u]++;edge[v]++;
}
}
void Tarjan(int u){
low[u]=dfn[u]=++t;
int cnt=0;
for(int i=0;i<g[u].size();i++){
int v=g[u][i];
if(!dfn[v]){
++cnt;
Tarjan(v);
if(u!=root&&low[v]>=dfn[u] || u==root&&cnt>1) cutpoint[u]=1;
low[u]=min(low[u],low[v]);
}
else low[u]=min(low[u],dfn[v]);
}
}
int main(){
freopen("tree.in","r",stdin);
freopen("tree.out","w",stdout);
init();
Tarjan(root);
for(int i=1;i<=n;i++) if(!cutpoint[i]&&m-edge[i]==n-2) ans[++newp]=i;
printf("%d\n",newp);
for(int i=1;i<=newp;i++) printf("%d ",ans[i]);
return 0;
}



