偶数个3|递归|递推

目录

• 偶数个3|递归|递推
  • Problem
  • 分析
  • Code
    • 递归
    • 递推

偶数个3|递归|递推

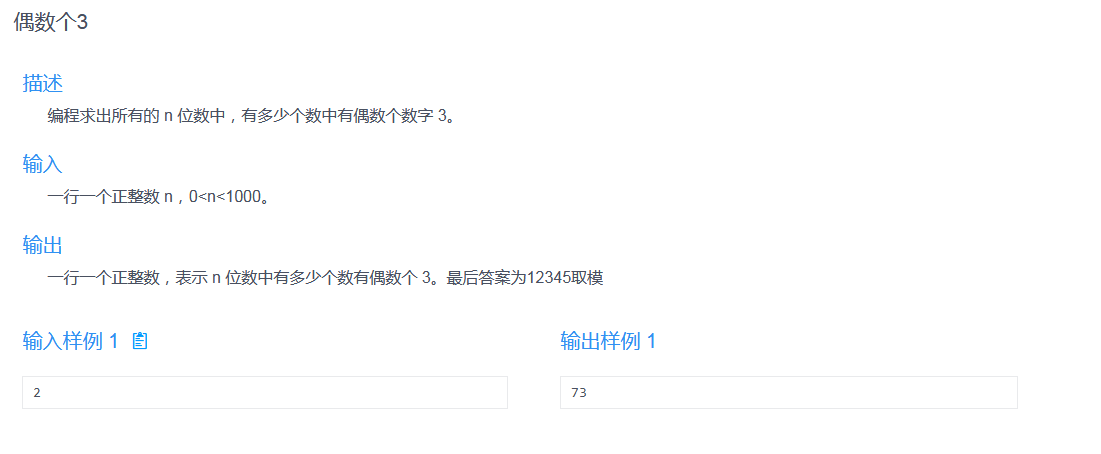
Problem

分析

n=1时：

偶数个3有8个（即未出现3），奇数个有1个。

n=2时：

对于十位，如果为3，则个位为3.

如果不为3，则个位也不为3，且这种情况有9种，乘法原理

f(n)表示n位数时偶数个3的个数

g(n)表示n位数时奇数个3的个数

f(1)=8,g(1)=1;

假设已经知道f(n-1),g(n-1)

求f(n):

1、第n位没有出现3

=>n-1位有偶数个3

=>一共有9种

==>f(n)=f(n-1)*9

2、第n位出现3

=>n-1位有奇数个3

=>f(n)=g(n-1)

求g(n):

同f(n)

Code

递归

#include <cstdio>
#include <iostream>
using namespace std;
const int maxn=1005;
int f1[maxn],g1[maxn];
int g(int n);
int f(int n){
	if(n==1) return f1[n]=8;
	return f1[n]=(f(n-1)*9%12345+g(n-1)%12345)%12345;
}
int g(int n){
	if(n==1) return g1[n]=1;
	return g1[n]=(g(n-1)*9%12345+f(n-1)%12345)%12345;
}
int main(){
	int n;cin>>n;
	cout<<f(n)%12345;
	return 0;
}

递推

#include <cstdio>
#include <iostream>
using namespace std;
const int maxn=1005;
long long f[maxn][2];//f[i][0]表示奇数 f[i][1]表示偶数 
int main(){
	int n;cin>>n;
	f[1][0]=8,f[1][1]=1;
	for(int i=2;i<=n;i++){
		f[i][0]=(9*f[i-1][0])%12345+f[i-1][1]%12345;
		f[i][1]=(f[i-1][1]*9)%12345+f[i-1][0]%12345;
	}
	cout<<f[n][0]%12345;
	return 0;
}