扩展欧几里得算法
定义:
贝祖定理对于任意整数a,b,存在一对整数x,y,满足ax+by=gcd(a,b)
用欧几里得算法计算一组x,y的方法,称作“扩展欧几里得”算法
求解
思路
假设a>b
\[(1) b=0:gcd(a,b)=a,ax+by=a,则x=1,y=0;
\]
\[(2)b\neq0,如图
\]
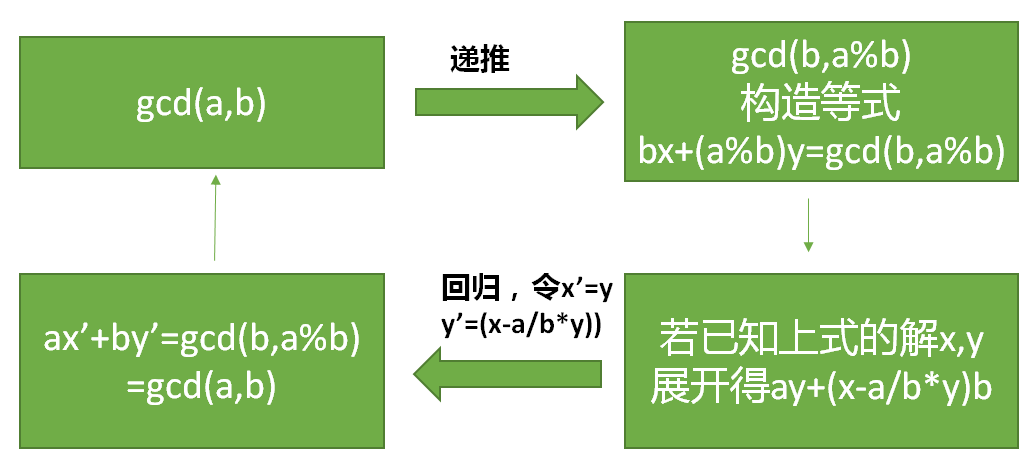
Code
int exgcd(int a,int b,int &x,int &y){//求解ax+by=gcd(a,b)x,y 并返回 最大公约数
if(b==0){
x=1,y=0;
return a;
}
int d=exgcd(b,a%b,x,y);
int tmp=x;x=y;y=tmp-(a/b)*y;
return d;
}
一般
对于ax+by=c 该方程有解当且仅当
gcd(a,b)|c
此时可先求ax+by=gcd(a,b)的解x',y',即ax'+by'=gcd(a,b),令d=gcd(a,b),等式两边同时乘以c/d可得原方程的一组解为:
\[\left\{\begin{matrix}x={x}'\cdot c/d
\\
y={y}'\cdot c/d
\end{matrix}\right.
\]
Ps:通解
\[\left\{\begin{matrix}x={x}'\cdot \frac{c}{d}+k\frac{b}{d}
\\
y={y}'\cdot \frac{c}{d}-k\frac{a}{d}
\end{matrix}\right.
\]
•通解说明:
•ax+by=c,令a(x+t1)+b(y+t2)=c,可得
•at1=-bt2,左右两边必须同时包含a,b的因子
•最小的满足上式的正整数为lcm(a,b)
•即
\[a\cdot t1=-b\cdot t2=k\cdot lcm(a,b)
\]
•则
\[t1=k \cdot \frac{lcm(a,b)}{a}=k\cdot \frac {\frac{a\cdot b}{gcd(a,b)}}{a}=k\cdot \frac{b}{gcd(a,b)}
\]
•
\[t2=-k \cdot \frac{lcm(a,b)}{a}=-k\cdot \frac {\frac{a\cdot b}{gcd(a,b)}}{a}=-k\cdot \frac{b}{gcd(a,b)}
\]
获得最小正解的方法:
令d=gcd(a,b);
首先获得一个解x':
\[x=x{'}\cdot \frac{c}{d}
\]
根据通解修正为正数:
\[x=(x\%\frac{b}{d}+\frac {b}{d})\%\frac{b}{d}
\]
得到另一个解y:
\[y=\frac{c-a*x}{b}
\]
应用
应用1:求解线性同余方程
1)什么是线性方程:
我们把一次方程(图像是直线)称作线性方程,比如O(n)算法常被称作线性时间。
2)什么是线性同余方程:
形如
\[ax\equiv b\left ( mod\ m \right )
\]
叫做线性同余方程。
3)求解思路:
方程等价于m|(ax-b),即ax-b是m的倍数,不妨设为-y倍。于是该方程改写为:ax+my=b
剩下的根据扩展欧几里得定理求解。
由欧几里得:有解时当且仅当gcd(a,m)|b
在有解时,先用欧几里得算法求出一整数x0,y0,满足
\[a \cdot x_0+m \cdot y_0=gcd\left( a,m \right)
\]
然后
\[x=x_0 \cdot b/gcd\left(a,m\right)
\]
就是原线性同余方程的一个解。
方程的通解则是所有模m/gcd(a,m)与x同余的整数。
获得最小正解的方法:
令d=gcd(a,b);
首先获得一个解x':
\[x=x{'}\cdot \frac{c}{d}
\]
根据通解修正为正数:
\[x=(x\%\frac{m}{d}+\frac {m}{d})\%\frac{m}{d}
\]
例题:青蛙约会
这篇博客
应用2:乘法逆元
1)概念:
若
\[b\cdot x \equiv 1\left(mod\ m\right)
\]
且b,m互质,则称x为b的逆元,记作
\[b^{-1}\left(不仅仅是\frac{1}{b} \right)
\]
2)作用:
根据可乘性,两边同时乘以a,再同除以b(因为b,m互质所以可以除),得
\[\frac{a}{b} \equiv a \cdot b^{-1} \left(mod \ m\right)
\]
可以看出,通过逆元可以把除法的求余运算变成乘法的求余运算。
3)求解思路:
方法一:(效率较高,常用)
显然,b,m互质时,对于
\[b\cdot x\equiv 1\left(mod \ m\right),gcd\left(b,m\right)=1|1
\]
满足线性同余方程有解的条件,所以可用扩展欧几里得算法求出x,即为b模m的逆元。
方法二:
显然,b,m互质时,根据欧拉定理可得
\[b^{\varphi \left(m\right)}=1\left(mod \ m\right)
\]
而
\[b^{\varphi \left(m\right)}=b\cdot b^{\varphi \left(m\right)-1}
\]
则
\[b^{\varphi \left(m\right)-1}
\]
为b模m的逆元
特别的,当m本身是质数的时候,由费马小定理(欧拉定理)可得
\[b^{m-1}\equiv 1\left(mod \ m\right)
\]
则
\[b^{m-2}
\]
就是b模m的逆元。




