Catalan数
Catalan 数
引入
Problem:
具有n个节点的二叉树的形态有多少种?
分析:
因为二叉树定义具有递归性,左子树有i个节点,那么右子树有n-i-1个节点,根据计数原理:
\[f\left ( n \right )=\sum_{i=0}^{n-1}f\left ( i \right )\cdot f\left ( n-i-1 \right ),f\left ( 0 \right )=1,f\left ( 1 \right )=1
\]
Catalan数
这里的:
\[f\left ( n \right )=\sum_{i=0}^{n-1}f\left ( i \right )\cdot f\left ( n-i-1 \right )
\]
就叫做卡特兰数,该数列的前若干项是:
1,2,5,14,42,132,429,1430....
所以增长速度是非常快的。
常见的Catalan数表达式
1、递推式:
\[f\left ( n \right )=\sum_{i=0}^{n-1}f\left ( i \right )\cdot f\left ( n-i-1 \right ),f\left ( 0 \right )=1
\]
2、另类递推式:
\[f\left ( n \right )=\frac{(4n-2)f\left ( n-1 \right )}{n+1}
\]
3、通向式(重要,常用):
\[f\left ( n \right )=\frac{C\begin{matrix}
n\\
2n
\end{matrix}}{n+1}
\]
4、通向式2:
\[f\left ( n \right )=C\begin{matrix}
n\\
2n
\end{matrix}
-C
\begin{matrix}
n-1\\
2n
\end{matrix}
\]
利用通向式求Catalan(n) Code
#define ll long long
ll Catalan(ll n){
ll ans=1;
for(ll i=n+1;i<=2*n;i++){
ans=ans*i/(i-n);
printf("%d %d %lld\n",i,i-n,ans);
}
return ans/(n+1);
}
应用:
•Cn表示n个节点不同形态的二叉树个数。
•Cn表示n的入栈序列对应的合法出栈序列的个数。(luogu P1044)
变式:
•n个0和n个1,构造一个长度为2n的序列,使得序列的任意前缀中1的个数不 少于0的个数,这样的序列有多少种?
•n个矩阵相乘,用括号改边运算顺序,有多少种?(ps:n个矩阵相乘需要n-1对括号,再增加是无意义的)
•游乐园门票1元一张,每人限购一张。现在有10个小朋友排队购票,其中5个小朋友每人只有1元的钞票一张,另5个小朋友每人只有2元的钞票一张,售票员没有准备零钱。问:有多少种排队方法,使售票可以正常进行下去?
•凸多边形分割成三角形方案数
图像法
n·n的矩阵,每次只能往右或往上走1个单位,问从(0,0)走到n·n,且路线一直处于y=x之下的方法总数是多少?
只需要n步的向右和n步的向上就能到达(n,n)。为了不跨越y=x,需任意时刻向右的次数>=向上的次数,显然答案就是卡特兰数。
扩展:几乎所有的卡特兰数的问题都可以用这样的折线法方式解答。比如入栈映射为向右,出栈映射成向上,任意时刻入栈次数>=出栈
例题-luogu P2532 [AHOI2012]树屋阶梯
Problem
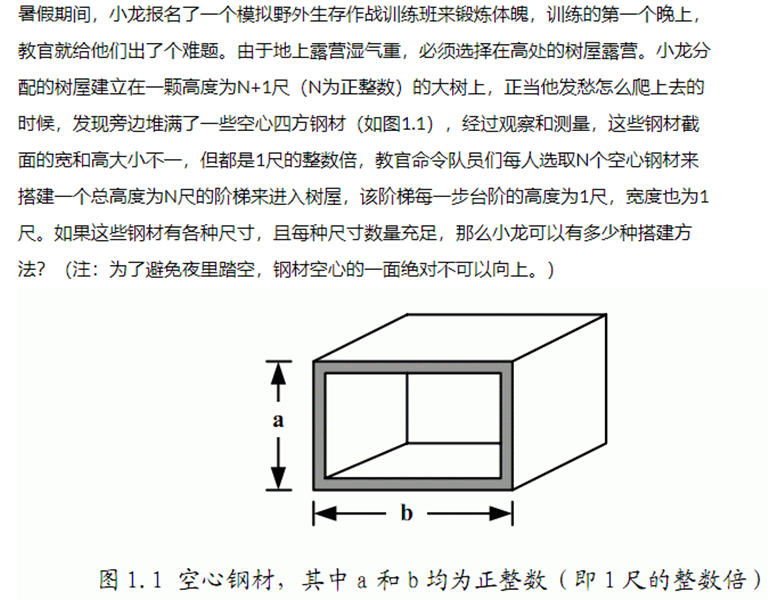
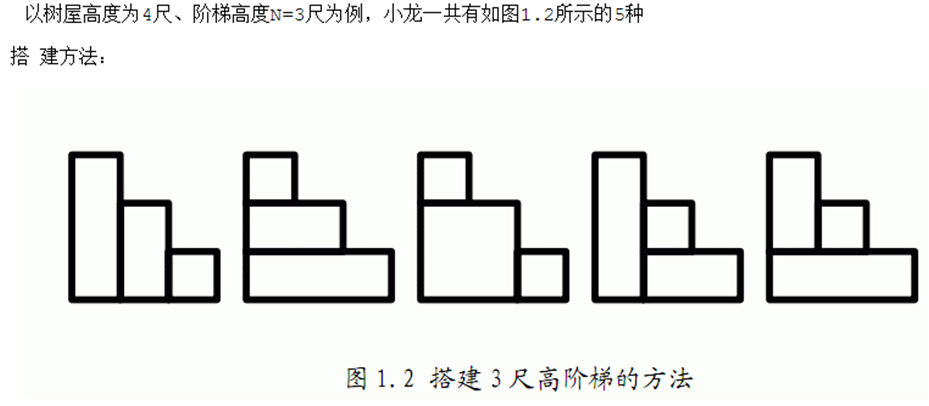
分析
卡特兰数,注意N的取值范围,要用高精度。
Code
#include <cstdio>
#include <iostream>
#define ll long long
using namespace std;
const int maxn=10005;
struct highprecc{
int l,a[maxn];
void init(){l=1;a[1]=1;}
void out(){for(int i=l;i>=1;i--) printf("%d",a[i]);}
highprecc operator * (const ll b) const{
highprecc c;
for(int i=1;i<=l;i++) c.a[i]=a[i]*b;
for(int i=2;i<=l;i++){
c.a[i]+=c.a[i-1]/10;
c.a[i-1]%=10;
}
c.l=l;
while(c.a[c.l]>10){
c.a[c.l+1]=c.a[c.l]/10;
c.a[c.l]%=10;
c.l++;
}
return c;
}
highprecc operator / (const ll b) const{
highprecc c;
ll k=l,g=0;
for(int i=l;i>0;i--){
g=g*10+a[i];
c.a[i]=g/b;
g%=b;
}
while(k>1 && c.a[k]==0) k--;
c.l=k;
return c;
}
};
highprecc f(ll n){
highprecc ans;ans.init();
for(ll i=n+1;i<=2*n;i++) ans=ans*i/(i-n);
return ans/(n+1);
}
int main(){
ll n;scanf("%lld",&n);
f(n).out();
return 0;
}


