板子|LCA倍增解法
LCA
定义
LCA(Lowest Common Ancestors),即最近公共祖先,是指在有根树中,找出某两个结点u和v最近的公共祖先。
重要结论
对于一棵树:
求两点x,y的距离:
dist=深度[x]+深度[y]-2*dep[LCA(x,y)];
倍增
解法
1、常规方法有哪些?
2、离线算法
3、倍增思想
认真分析会发现:
①常规的方式每次向上跳一步太慢了
②每一个状态的转移规则都是相同的。
能否预处理出i号节点向上的j辈的祖先呢?(问题:超空间,超时间)
所以能否利用倍增,来加速转移,缩小空间呢?
——>
类似ST算法,定义状态f[i][j],代表从i号节点向上跳2^j步到达的节点。
特殊的,如果跳到“外边”去了,则f[i][j]=0,f[i][0]
为i的父节点,其他情况:
f[i][j]=f[f[i,j-1],j-1]
按怎样的顺序预处理呢?
——>
基于f数组,对于x,y的LCA:
1、 BfS出每个节点的深度(假如x在更深的层次),并预处理f数组
2、 利用倍增将x,y调整到问样的高度。方法:每次尝试从x向上走2^k步(k取log2n...3,2,1),检查到达的节点是不是还是比y深,如果是则令x=f[x][k](思考:
如果走8步还是比y深,下一次为什么只考虑走4步?)
3、 第二步结束以后可能有两神情况:
①(说明y是x的某个祖先)
②x,y处在问一层,此时再利用
第二步的方式一起往上跳(You酱普,j酱普)。
板子题目
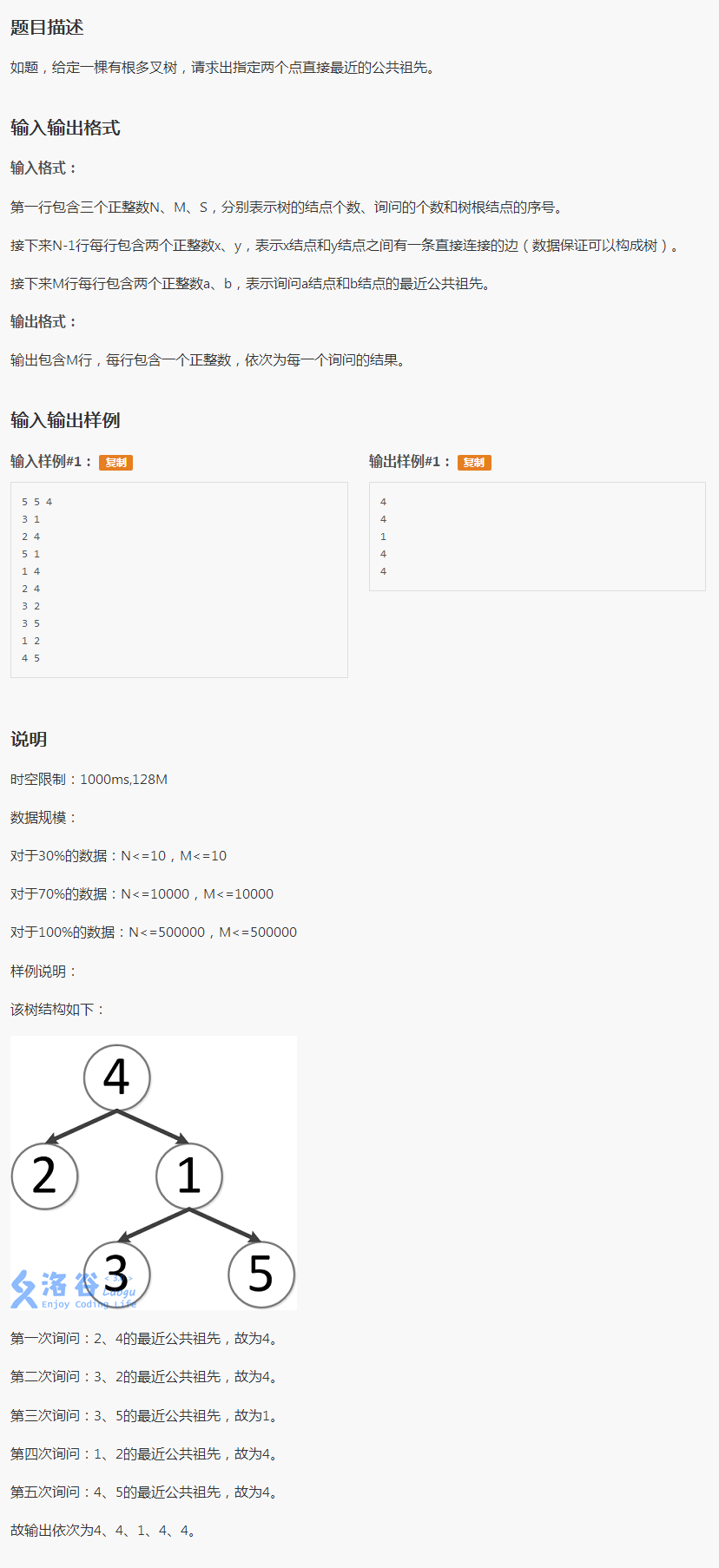
板子
P.S. luogu要开氧气才能过最后3个点,我太弟弟了
#include <cstdio>
#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>
#include <cmath>
using namespace std;
void read(int &n){
int num=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-') w=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
num=num*10+ch-'0';
ch=getchar();
}
n=num*w;
}
const int maxn=500005;
int n,m,s;
int dep[maxn],f[maxn][50];
int H;
vector<int> g[maxn];
void init(){
read(n);read(m);read(s);
for(int i=1;i<n;i++){
int u,v;read(u);read(v);
g[u].push_back(v);
g[v].push_back(u);
}
H=log(n);
}
void bfs(int s){
queue<int> q;
q.push(s);dep[s]=1;
while(!q.empty()){
int u=q.front();q.pop();
for(int i=0;i<g[u].size();i++){
int v=g[u][i];
if(dep[v]) continue;
q.push(v);
dep[v]=dep[u]+1;
f[v][0]=u;//父亲节点
for(int j=1;j<=H;j++) f[v][j]=f[f[v][j-1]][j-1];
}
}
}
int LCA(int x,int y){
if(dep[x]<dep[y]) swap(x,y);
for(int i=H;i>=0;i--)//将x,y移到同一深度
if(dep[f[x][i]]>=dep[y]) x=f[x][i];
if(x==y) return x;//特判
for(int i=H;i>=0;i--){
if(f[x][i]!=f[y][i]){
x=f[x][i];
y=f[y][i];
}
}
return f[x][0];
}
void solve(){
for(int i=1;i<=m;i++){
int u,v;read(u);read(v);
printf("%d\n",LCA(u,v));
}
}
int main(){
init();
bfs(s);
solve();
return 0;
}



